8. シンプレクティック法
もちろん、数値積分できることの意義は、解析解がない方程式でも答を求めら
れる、ということなんだけど、そうなるとじゃあ答は正しいのか、ということ
になって、その話はあとでもうちょっと詳しくするのでもうちょっと線型方程
式でね。
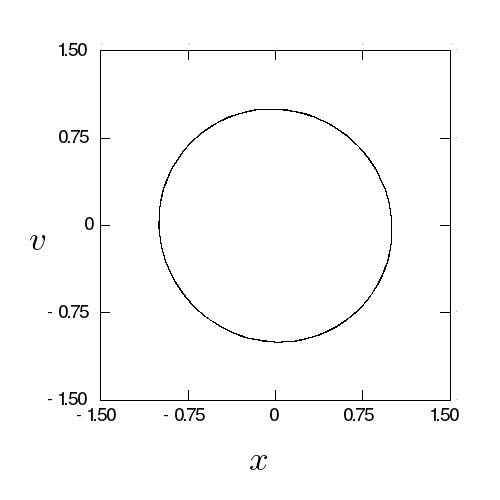
ちょっとオイラー法に話を戻すわね。前の、オイラー法で軌道プロットする
学生C:えーと、これどういう意味でしょうか? x を更新して、その更新した
x を使って v を更新するわけですね?精度は同じじゃないんですか?
赤木 :まあとりあえずやってみて。
学生C:はい、、、え、なんかこれ間違ってないですか?
図 7 ですが、10回転のはずなのに線が一本で、、、
赤木 : ここまで、線形の方程式ばっかりで、解析答があるのでそもそもなぜ数値
計算するのかしらという疑問もあったと思うんだけど、もうちょっと我慢して
ね。線形の方程式のメリットはまさにその答がわかっている、ということで、
数値積分法の特徴がわかりやすいから。
require "grlib"
include Math
include GR
x=1.0; v=0.0; k=1.0
n=ARGV[0].to_i
norb=ARGV[1].to_i
wsize=ARGV[2].to_f
h = 2*PI/n
p! h
t=0
setwindow(-wsize, wsize,-wsize, wsize)
box
setcharheight(0.05)
mathtex(0.5, 0.06, "x")
mathtex(0.06, 0.5, "v")
(n*norb).times{
xp=x
vp=v
dv = -x*k*h
x+= v*h
v+= dv
t+= h
polyline([xp,x], [vp,v])
}
p! [x, v, t]
p! [x-cos(t), v-sin(t)]
gets
だけど、
xp=x
vp=v
dv = -x*k*h
x+= v*h
v+= dv
t+= h
のところ、
xp = x
vp = v
x+= v*h
v+= -x*k*h
t+= h
にして、n=100, 10回転とかでグラフ書いてみて。
赤木 : これ、実はこれであってるの。 6 でやったみ たいに、 行列で書いてなんかしてみて?
学生C:えーと、
赤木 :ここからは線型代数の力に頼ることにして、まず固有方程式ね。固有
方程式は?
学生C:えーと、
学生C:えーと、
赤木 :そう。なので、
学生C:
赤木 :そう。だから、固有ベクトルの空間で考えると、この数値積分法で調
和振動子を積分することはそれぞれの要素に絶対値が1の共役な複素数を掛け
ることになってるわけ。
なので、固有ベクトルの空間では、2つの要素がそれぞれ逆方向に円運動する
わけね。元の空間ではどうなるかわかるかしら?
学生C:楕円とかですか?
赤木 :なんかあてずっぽう感があるけど、そうね。実数の解がいるけ
ど、これは複素共役な値が解になってるから、2つを足せばいいの。
この辺、実際に頑張って計算すれば確認できるけど、線型空間とか対角化とか
の性質から、実際に要素とか計算しなくてもわかる、というのが大事ね。
学生C:でもどういう楕円なんですか?
赤木 :固有ベクトルちゃんと求めてその座標系での円が元の座標系でどうな
るか出すのでも求まるけど、楕円の方程式は
学生C:それは読者の演習問題ということですね?
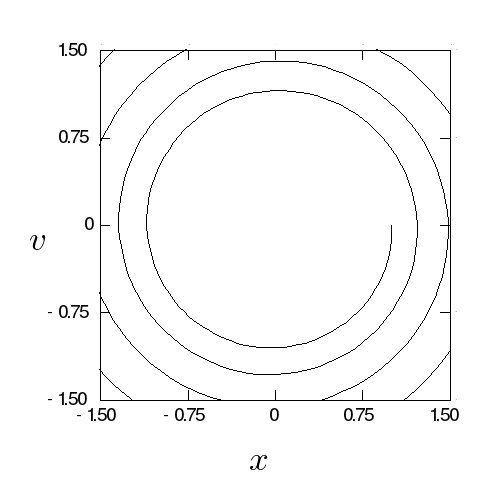
赤木 :まあじゃあそういうことで。ところで、この方法での解なんだけど、
確かにオイラー法みたいにどんどんずれるわけではないけど、もちろんちゃん
と円軌道になるわけでもないのね。そのことは、上の楕円が楕円であって
円ではないことと、計算すればわかるけど楕円の円からのずれがこの方法では
h に比例することからわかるわけ。
なので、もっと正確に軌道を求められる、精度のよい方法はないか、というの
がここからの話ね。
学生C:なんか2次とか4次のルンゲクッタみたいなのがないか、ということで
すよね?
赤木 :そう。で、もちろん、ルンゲクッタでは駄目なのね。上の方法は
学生C: はあ、そうですけど、、、
赤木 :これね、誤差のでる向きが逆になるの。ちょっとちゃんと調べてみて?
学生C:ちょっと雑ですが作ってみました:
学生C:えーと、例えば
赤木 :
学生C:
赤木 :そうね。これもう i+1 なくなってるから、今 i+2 となってるのを
i+1 と思うことにして、
学生C:えーと、、、、
であってますか?
赤木 :これ、 x のほうは
学生C:適当ですが
赤木 :そうね。これ、あとの都合もあるから、3つの積分法ちゃんと関数にし
てみて。自律型方程式用として x,v,h,f を受け取って x,v 返すものにしましょ
う。で、前の章と同じように誤差をだしてみて。誤差は、積分している間の
x, v の誤差をベクトルとして絶対値にして、その最大値にしてみて。
学生C:何か注文が多いですが、、、えーと、
赤木 :あ、いい感じね。じゃあついでにもっと高次にいきましょう。
4次の公式を書くと、こんな感じなの。
学生C : あのー、意味がわからないんですけど、、、、。
赤木 ::あ、これはね、
これ、戻る量を進む量の
で、さらに6次の公式ってのもあって、国立天文台におられた吉田春夫先生
が導いた、
学生C:3回呼ぶんですね。こんなのですかね?
赤木 :そうね、ちゃんとできた気がするので、今回この辺で。
ちなみ、今回やったようなのを「シンプレクティック積分法」というのね。
シンプレクティックってのはどういう意味かというと、これ解析力学やったら
「正準変換」というのを習ったはずなんだけど、数値積分法が「正準変換」
になっている、ということ。正準変換って、大雑把な意味としては、
その変換によって物理系が変わらない、つまり、
変換してから時間積分して元に戻しても、もとの系を時間積分しても、
同じ解になる、ということで、それがそれが無限に時間たってもなりたつよう
な数値積分法なわけ。まあそうするとなんかいいことがありそうでしょ?
で、今回みたように実際にある、というのがわかってるわけ。
システム数理IV講義資料 http://jun-makino.sakura.ne.jp/kougi/system_suuri4_1999/overall.html
Recent Progress in the Theory and Application of Symplectic
Integrators, H. Yoshida 1993,
https://link.springer.com/chapter/10.1007/978-94-011-2030-2_3
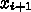 があるから、これを
があるから、これを
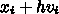 で置き換えると
で置き換えると
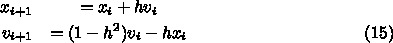
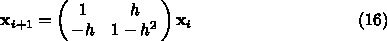
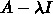 の行列式でよかったでしたっけ?
の行列式でよかったでしたっけ?
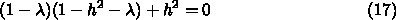

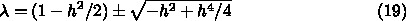
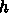 が1より小さいからですか?
が1より小さいからですか?
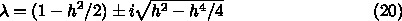
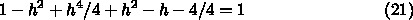
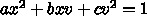 だから
それが時間積分で不変になるような a, b, c を求めてみればいいわけ。
だから
それが時間積分で不変になるような a, b, c を求めてみればいいわけ。

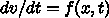 で、以下面倒
なので自律系でいいのかな、 tがないやつね、での話とすると、
で、以下面倒
なので自律系でいいのかな、 tがないやつね、での話とすると、


require "grlib"
include Math
include GR
n=ARGV[0].to_i
norb=ARGV[1].to_i
wsize=ARGV[2].to_f
h = 2*PI/n
p! h
setwindow(0, norb,-wsize, wsize)
box
setcharheight(0.05)
mathtex(0.5, 0.06, "t/2\\pi")
mathtex(0.06, 0.5, "err")
def symplectic1(x,v,t,k,h)
x+= v*h
v+= -x*k*h
t+= h
{x,v,t}
end
def symplectic2(x,v,t,k,h)
v+= -x*k*h
x+= v*h
t+= h
{x,v,t}
end
2.times{|i|
x=1.0; v=0.0; k=1.0; t=0.0
xdata=[0.0]
ydata= [x-cos(t)]
(n*norb).times{
if i==0
x,v,t=symplectic1(x,v,t,k,h)
else
x,v,t=symplectic2(x,v,t,k,h)
end
xdata.push t/(2*PI)
ydata.push x-cos(t)
}
polyline(xdata, ydata)
setlinetype(2)
}
gets
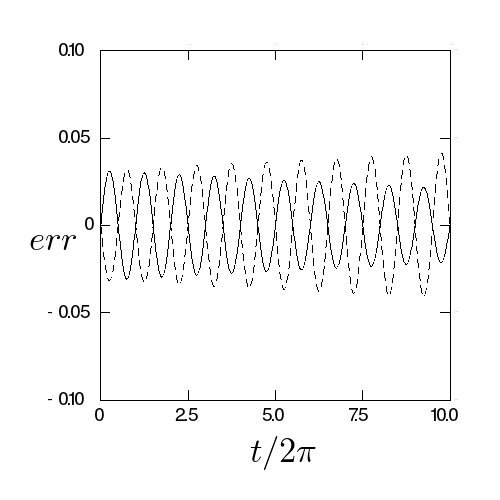
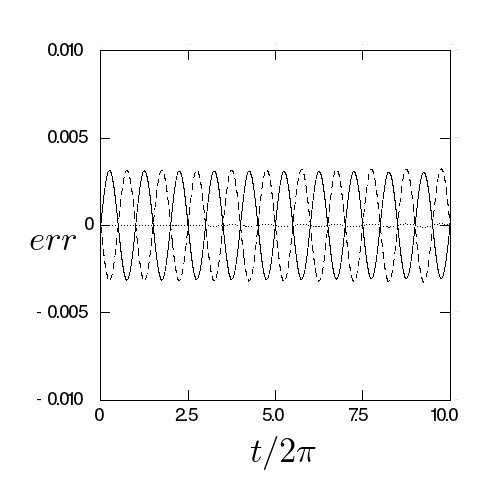
赤木 :まあ段々ずれるけど、最初は綺麗に逆でしょ?だから、毎回この2つを
繰り返す、ってのが考えられるじゃない。どういう計算になるかしら?


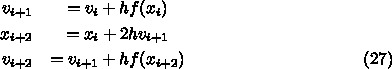
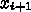 はでてこなくなりますね。
はでてこなくなりますね。
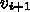 も消してみて?
も消してみて?
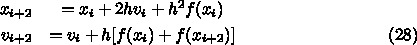
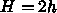 として書換えて、書換えたあとで H を
h に戻してみて?
として書換えて、書換えたあとで H を
h に戻してみて?
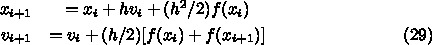
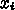 のところでのテイラー展開の2次までとっ
てて、vは台形公式ね。なので、あってるはず。これもさっきのグラフに追加
してみて?あ、ちなみに、この積分方法はリープフロッグ(蛙飛び)って名前な
の。
のところでのテイラー展開の2次までとっ
てて、vは台形公式ね。なので、あってるはず。これもさっきのグラフに追加
してみて?あ、ちなみに、この積分方法はリープフロッグ(蛙飛び)って名前な
の。
require "grlib"
include Math
include GR
n=ARGV[0].to_i
norb=ARGV[1].to_i
wsize=ARGV[2].to_f
h = 2*PI/n
p! h
setwindow(0, norb,-wsize, wsize)
box
setcharheight(0.05)
mathtex(0.5, 0.06, "t/2\\pi")
mathtex(0.06, 0.5, "err")
def symplectic1(x,v,t,k,h)
x+= v*h
v+= -x*k*h
t+= h
{x,v,t}
end
def symplectic2(x,v,t,k,h)
v+= -x*k*h
x+= v*h
t+= h
{x,v,t}
end
def symplectic2(x,v,t,k,h)
v+= -x*k*h
x+= v*h
t+= h
{x,v,t}
end
def leapfrog(x,v,t,k,h)
f0 = -x*k
x+= v*h + f0*(h*h/2)
f1 = -x*k
v+= (f0+f1)*(h/2)
t+= h
{x,v,t}
end
3.times{|i|
x=1.0; v=0.0; k=1.0; t=0.0
xdata=[0.0]
ydata= [x-cos(t)]
(n*norb).times{
if i==0
x,v,t=symplectic1(x,v,t,k,h)
elsif i==1
x,v,t=symplectic2(x,v,t,k,h)
else
x,v,t=leapfrog(x,v,t,k,h)
end
xdata.push t/(2*PI)
ydata.push x-cos(t)
}
polyline(xdata, ydata)
setlinetype(i+2)
}
gets
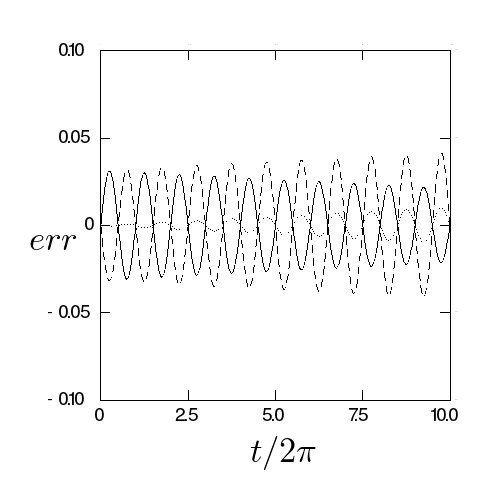
setlinetype に数字入れるとなんか線変わるみたいなので、適当な数字いれて
ます。点線がリードフロッグですね。時間刻みを 1/10 に小さくすると、
前の2つの公式は誤差が大体 1/10 になってますが、リープフロッグは
それよりもずっと小さくなってるので、多分ちゃんと時間刻みの2乗になって
るのではと。
require "grlib"
include Math
include GR
def symplectic1a(x,v,h,f)
x+= v*h
v+= f.call(x)*h
{x,v}
end
def symplectic1b(x,v,h,f)
v+= f.call(x)*h
x+= v*h
{x,v}
end
def leapfrog(x,v,h,f)
f0 = f.call(x)
x+= v*h + f0*(h*h/2)
f1 = f.call(x)
v+= (f0+f1)*(h/2)
{x,v}
end
def harmonic(x,k)
-k*x
end
setwindow(3e-5, 7e-2, 1e-8, 1e-1)
setscale(3)
box(x_tick:100,y_tick:100,major_y:2,xlog: true, ylog: true)
k=1.0
ff = -> (xx : Float64){ harmonic(xx,k)}
lt=1
["S1A", "S1B", "LF"].each{|name|
n=100
print "Result for ", name, " method\n"
ha=Array(Float64).new
ea=Array(Float64).new
10.times{
h=1.0/n*PI
t=0.0
x=1.0
v=0.0
emax = 0.0
h = 2*PI/n
p! h
while t < 10*PI*2 - h/2
if name == "S1A"
x, v = symplectic1a(x,v,h,ff)
elsif name == "S1B"
x, v = symplectic1b(x,v,h,ff)
else
x, v = leapfrog(x,v,h,ff)
end
t+= h
ex = x-cos(t)
ev = v+sin(t)
eabs=sqrt(ex*ex+ev*ev)
emax = eabs if eabs > emax
end
ha.push h
ea.push emax
n*=2
}
p! ha
p! ea
setlinetype(lt)
polyline(ha, ea)
lt+=1
}
setcharheight(0.04)
mathtex(0.5,0.07,"\\Delta t")
mathtex(0.02,0.5,"\\rm Err ")
mathtex(0.4,0.55,"\\rm S1A")
mathtex(0.5,0.75,"\\rm S1B")
mathtex(0.4,0.25,"\\rm Leapfrog")
c=gets
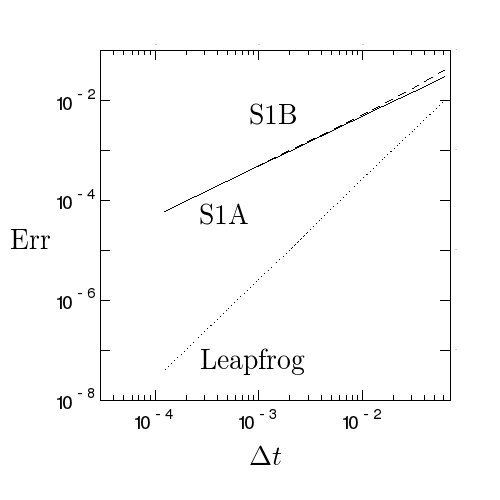
こんなふうになりました。
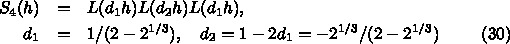
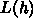 がステップ h のリープフロッグで1ス
テップだけ積分するってこと。だから、リープフロッグでまずちょっと行き過
ぎて、次に逆に戻って、最後に最初と同じだけ進んで次の時刻に行くというふ
うになってるわけ。
がステップ h のリープフロッグで1ス
テップだけ積分するってこと。だから、リープフロッグでまずちょっと行き過
ぎて、次に逆に戻って、最後に最初と同じだけ進んで次の時刻に行くというふ
うになってるわけ。
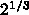 倍にしているのね。
なぜそうするかというと、リープフロッグはx も v も時間刻みの2次まで
とってることになるから、1ステップの誤差は3次なのね。だから、
2回目で戻る時の誤差は進む時の2倍になるから、進むのは2回でうちけしてく
れないか、ということなわけ。こんなので上手くいくのかと思うけど、
うまくいくのよ。
倍にしているのね。
なぜそうするかというと、リープフロッグはx も v も時間刻みの2次まで
とってることになるから、1ステップの誤差は3次なのね。だから、
2回目で戻る時の誤差は進む時の2倍になるから、進むのは2回でうちけしてく
れないか、ということなわけ。こんなので上手くいくのかと思うけど、
うまくいくのよ。

def yoshida4(x,v,h,f)
d1 = 1.0 / (2-exp(log(2.0)/3))
d2 = 1 - 2*d1
x,v= leapfrog(x,v,h*d1,f)
x,v= leapfrog(x,v,h*d2,f)
leapfrog(x,v,h*d1,f)
end
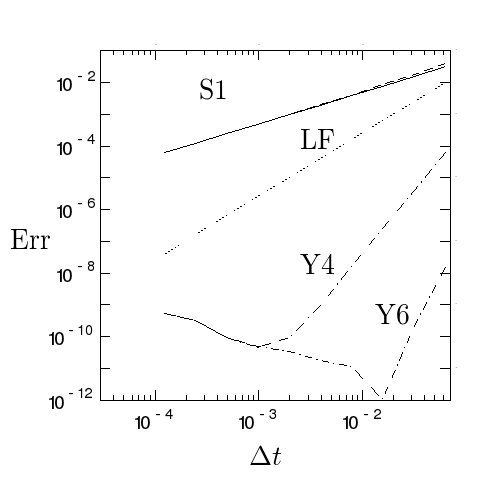
もうちょっと賢く書ける気がするのと、d1 とか d2 毎回計算しているのは
よくない気がしますが、、、あと6次も作りました。結果は
13 で、大丈夫な感じがします。
8.1. 課題
8.2. まとめ
8.3. 参考資料