4. 放物型方程式
物理・天文で出てくる偏微分方程式は大抵は 2 階である。で、普通は空間3次 元と時間1次元の4次元空間で定義されるわけだが、この講義ではいくつかの特 殊な場合を除いて空間1次元時間1次元の2次元で考える。 これは、そうしておかないとプログラムを書くのも、また計算機のほうも大変 になるからである。
放物型方程式ってのは何か?というのは皆さん知っているはずなので(だよね?) 厳密な定義は省くが、要するに以下の形に書ける(移流)拡散方程式のことで ある。

ここで x, t はそれぞれ空間、時間を表す変数であり、 u は方程式が 記述する量である。拡散方程式として見ればなにかの濃度ということになるし、 熱伝導の方程式としてみれば温度なりエンタルピーなりということになる。 K は一次の係数で、これは普通の拡散方程式や熱伝導方程式では 0 である。 これが 0 でないのはどういう場合かというのは後でちょっと考える。 D が 普通の拡散係数ということになる。今は D が空間・時間に依存しない場合 を考える。
依存しない場合はもちろん変数分離で解けるので、数値計算することに意味が あるのはD が空間・時間に依存する場合だが、まあ、とりあえずは答がわか る場合を計算してみることにしよう。
放物型方程式の場合には、初期条件と境界条件を与えないと解が定まらない。 以下では、
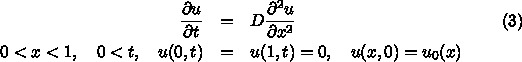
偏微分方程式の数値計算の方法は基本的には有限要素法と差分法に大別される。
あ、あとスペクトラル法というのもあるが、これはちょっとおいておく。
有限要素法の考え方はだいぶややこしいので、まず差分法を考える。
差分法とは、基本的には微分方程式に出てくる空間微分や時間微分の項を、差
分で置き換えるものである。差分というのはそもそも何かというのを説明
しないといけない。
例えば区間
なお、差分のとり方は一意的ではないことに注意して欲しい。例えば、
さて、拡散方程式なので2階微分がいる。これはどう作ればいいかというわけ
だが、これはむしろ一般に高階微分を差分で表す、つまり数値微分の方法を説
明しておくほうが簡単であろう。
初期条件は
なお、面倒なので
コンパイルには
なお、環境変数 GKS_WSTYPE を mp4 にすることで動画ファイルを作成できる。
また、
画面に出す時には環境変数 GKS_DOUBLE_BUF を設定する(値は1とかtrueとか適
当に)と、画面のチラツキがなくなる。
ここまでで、拡散方程式に対するもっとも簡単な差分近似である、空間微分
具体的には、拡散方程式なので本来は次第に滑らかになっていくべきなのに、
どんどんガタガタになってしまう。しかも、これは
まず、なぜそういう振動が起きるのかを考え、それから振動を起こさない方法
があるのかどうかを議論していこう。
さて、まず、なぜ振動が起きるかということだが、これは原理的には差分化さ
れた方程式の固有値を求めればわかる。
つまり、
この行列は実対称行列なので固有値分解ができて、適当なユニタリ行列
このように分解できるので、
不安定性が起きないための条件は、全ての固有値
さて、そういうわけで、固有値
断るまでもないと思うが、これは元の偏微分を変数分離して空間方向の関数に
ついての常微分方程式を導くのとほとんど同じ操作になっている。これを
線形差分方程式なので、解は
真面目にやるには境界条件を満たす固有ベクトルをもとめないといけないが、
面倒なので無限遠境界の場合を考える。この時、
なお、有限の固定境界の場合も結局境界条件を満たすような解を作るためには
このとき、式 (16)は
上でやったことは、結局空間方向をフーリエ級数展開して、各空間波長に対す
る時間発展が安定である(減衰していく)ことを要求しているのと同じである。
このようなやり方を von Neumann の方法による安定性解析という。
上の議論からわかるように、不安定条件に関係する
前節の議論から、初めに作ったプログラムでまともな答が求まるためには、
実は、なんとかなる方法というのはある。これが陰解法(implicit method)と
いうものである。拡散方程式の場合、もっとも簡単な陰解法は、空間微分に
線形連立方程式を解かないといけないのはもちろん面倒なわけだが、それだけ
のことはある。先ほどと全く同じように
陽解法と同じように行列で書いてみると、
具体的には、
一応、3重対角行列を解くプログラム全体を与えておくと、
係数の ad 等を計算して、1ステップ進める関数全体は、
4.1. 差分法
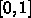 を
を 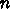 等分して、
等分して、 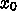 から
から 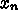 まで
(
まで
(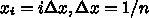 )で表すとする。時間も同様に、 <$t_j =
j\Delta t$> として、これから求める近似解
)で表すとする。時間も同様に、 <$t_j =
j\Delta t$> として、これから求める近似解 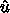 を簡単のため単に
を簡単のため単に
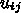 と書く。だいぶ記号が繁雑になるので、図 3 に
様子を書いておく。
と書く。だいぶ記号が繁雑になるので、図 3 に
様子を書いておく。
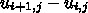 といった具合に隣との差を
とることである。微分を差分で近似するには、例えば
といった具合に隣との差を
とることである。微分を差分で近似するには、例えば
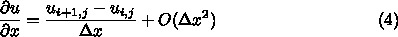
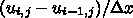 でもいいし、
でもいいし、
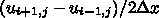 といったものも考えられる。さらに、もっ
と沢山の点を使うことも原理的には可能である。
といったものも考えられる。さらに、もっ
と沢山の点を使うことも原理的には可能である。
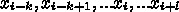 の
の 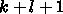 点での関数値
点での関数値
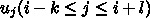 をつかって、点
をつかって、点 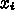 での
での 階導関数の近似値を求める考え方は以下
のようなものである。
階導関数の近似値を求める考え方は以下
のようなものである。
2階導関数を作るためには最低3点いるので、まずもっとも簡単な以下の形を使っ
てみる。
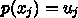 を満たす
を満たす 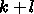 次補間多項式
次補間多項式 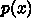 を作る。
を作る。
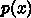 を
を  回微分する。
回微分する。
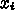 を代入する。
を代入する。
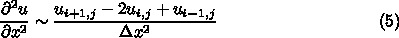

4.2. プログラム
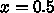 のところ
にだけ値がある
のところ
にだけ値がある 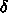 関数的なものということにする。
関数的なものということにする。
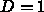 ということにする。時間の単位が
ということにする。時間の単位が 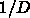 と思えば同
じことである。
と思えば同
じことである。
1:// program parabolic1
2:
3:#define _USE_MATH_DEFINES
4:#include <iostream>
5:#include <unistd.h>
6:using namespace std;
7:#include <cmath>
8:#include <gr.h>
9:
10:void initparam(double u[],
11: int & nx,
12: double &dx,
13: double & dt,
14: int & niter,
15: int &gmode)
16:{
17: cerr << "Enter nx, tmax, dt:";
18: double tmax;
19: cin >> nx >> tmax >> dt;
20: dx = 1.0/nx;
21: niter = (tmax+dt/2)/dt;
22: cerr << "Enter graphics mode 0: no G\n"
23: << " 1: animation\n"
24: << " 2: no-erase)\n";
25: cin >> gmode;
26: cout << "nx = " << nx<< " dt = " << dt << " niter = "<< niter<< "\n";
27: cout << "gmode = " << gmode << "\n";
28: int i;
29: for (i=0;i<=nx; i++) u[i] = 0;
30: u[(nx+1)/2] = nx;
31:}
32:
33:void push_system(double u[],
34: double unew[],
35: int nx,
36: double dx,
37: double dt)
38:{
39: double lambda = dt/(dx*dx);
40: int i;
41: for (i=1; i<nx; i++){
42: unew[i] = u[i] + lambda*(u[i-1]-2*u[i]+u[i+1]);
43: }
44: for(i=1; i<nx; i++){
45: u[i] = unew[i];
46: }
47:}
48:
49:
50:void show_graphics(double u[],
51: int nx,
52: double dx,
53: int gmode,
54: double xmin,
55: double xmax,
56: double ymin,
57: double ymax,
58: int first)
59:{
60: if (gmode == 0) return;
61: double x[nx+1];
62: if (gmode == 1) {
63:gr_clearws();
64: }
65: int i;
66: for(i=0;i<nx+1;i++){
67:x[i]=(i*dx);
68: }
69: gr_setwindow(xmin,xmax,ymin,ymax);
70: gr_axes(0.25*(xmax-xmin), 0.25*(ymax-ymin), 0, 0, 1, 1, -0.01);
71: gr_polyline(nx+1,x, u);
72: if (gmode == 1) usleep(30000);
73: gr_updatews();
74:}
75:
76:int main()
77:{
78:#define NMAX 10001
79: static double u[NMAX], unew[NMAX];
80: double dx, dt;
81: int nx, niter, gmode, iter;
82: initparam(u, nx, dx, dt, niter, gmode);
83: show_graphics(u, nx, dx, gmode, 0.0, 1.0, 0.0, 10.0, 1);
84: for(iter = 1; iter <=niter; iter++){
85: push_system(u, unew, nx, dx, dt);
86: show_graphics(u, nx, dx, gmode,0.0, 1.0, 0.0, 10.0, 0);
87: }
88: cerr << "Enter any key to finish:";
89: char c;
90: cin>>c;
91: return 0;
92:
93:}
これをちょっと動かしてみよう。
g++ parabolic1.cpp -o parabolic1 -std=c++11 -I $GRDIR/include\
-L $GRDIR/lib -Wl,-rpath,$GRDIR/lib -lGR
(既に書いた通り、 -I や -l 以下はライブラリをインストールした場所等に
依存する)
4.3. 安定性
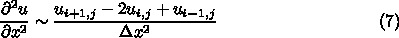

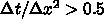 になると「うまく動かない」。
になると「うまく動かない」。
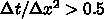 であれば
であれば 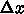 や
や 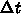 をどんなに小さくしても起こる。
をどんなに小さくしても起こる。
4.3.1. 線形安定性解析
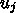 を時刻
を時刻 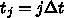 での数値解をベク
トルとして書いたものだとすると、差分近似は、
での数値解をベク
トルとして書いたものだとすると、差分近似は、

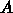 は
は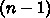 次元正方行列で、その各要素は差分近似の形から決
まる。この場合には、対角要素とその両側一列以外の全ての要素が 0 である3
重対角行列といわれる形をしている。要素の値は
次元正方行列で、その各要素は差分近似の形から決
まる。この場合には、対角要素とその両側一列以外の全ての要素が 0 である3
重対角行列といわれる形をしている。要素の値は
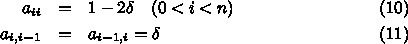
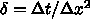 である。
である。
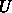 を持っ
てきて
を持っ
てきて

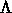 は固有値行列、つまり対角要素が固有値でそれ以
外が 0の行列である。
は固有値行列、つまり対角要素が固有値でそれ以
外が 0の行列である。
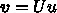 とすれば最初の差分近似式は
とすれば最初の差分近似式は


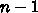 個の独立な方程式になって、解も自明に求まる。いうまでもな
いが、
個の独立な方程式になって、解も自明に求まる。いうまでもな
いが、 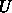 の各列は A の固有ベクトルになっている。つまり、
の各列は A の固有ベクトルになっている。つまり、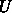 の
の 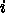 行
目を
行
目を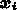 と書くと、
と書くと、

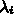 の絶対値が
の絶対値が
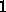 を超えないということである。
を超えないということである。
4.3.2. 固有値を求める
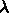 がどうなっているか調べてみよう。
式 14 をもともとの差分近似に入れてちょっと変形する
と、
がどうなっているか調べてみよう。
式 14 をもともとの差分近似に入れてちょっと変形する
と、
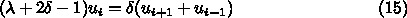
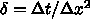 である。さらに、
である。さらに、


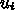 についての差分方程式と見て解を求めることを考える。
についての差分方程式と見て解を求めることを考える。
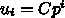 の形である。これを代入すると
の形である。これを代入すると


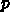 が実数のものはどち
らかで無限大に発散するのでよろしくないので、複素数の場合を考える。この
時は
が実数のものはどち
らかで無限大に発散するのでよろしくないので、複素数の場合を考える。この
時は 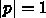 になっているので無限遠でも発散しない。
になっているので無限遠でも発散しない。
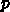 が複素数でないといけないことがすぐにわかる。このため、
が複素数でないといけないことがすぐにわかる。このため、  だけを考えればよい。
だけを考えればよい。

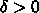 なので、
なので、 なるある
なるある 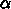 に
ついて
に
ついて であるためには、結局
であるためには、結局

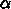 についてなり立つためには
についてなり立つためには


4.3.3. 「直観的」説明
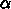 の値は実際には
の値は実際には
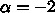 だけで、それ以外の
だけで、それ以外の 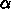 からはもっと緩い条件しかでな
い。
からはもっと緩い条件しかでな
い。 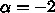 は
は 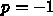 に対応するので、これは結局
に対応するので、これは結局 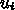 と
と
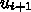 で値が逆転するようなパターンである。そのようなパターン(モー
ド)が 1
ステップ計算するとどうなるかをもう一度もとの差分式に戻って書き直してみ
ると、結局
で値が逆転するようなパターンである。そのようなパターン(モー
ド)が 1
ステップ計算するとどうなるかをもう一度もとの差分式に戻って書き直してみ
ると、結局
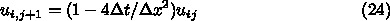

4.4. 陰解法
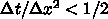 でないといけないということがわかっ
た。これは結構厳しい条件である。というのは、空間刻みの数を増やすと、その2
乗に比例して時間刻みの数を増やさないといけないので、全体としては空間刻
みの数の3乗に比例して計算時間がかかるということになるからである。まあ、
最近の計算機は速いので待てなくもないかもしれないが、もうちょっとなんと
かならないかという気もする。
でないといけないということがわかっ
た。これは結構厳しい条件である。というのは、空間刻みの数を増やすと、その2
乗に比例して時間刻みの数を増やさないといけないので、全体としては空間刻
みの数の3乗に比例して計算時間がかかるということになるからである。まあ、
最近の計算機は速いので待てなくもないかもしれないが、もうちょっとなんと
かならないかという気もする。
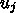 ではなく
ではなく 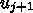 のほうを使う、つまり、
のほうを使う、つまり、
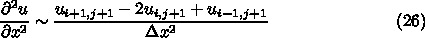
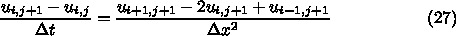
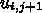 は左辺に単独で現れ、右辺は時刻
は左辺に単独で現れ、右辺は時刻 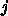 の項だ
けだったので、
の項だ
けだったので、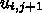 を直接計算できた。このように、直接計算できる
方法のことを陽解法 explicit method という。これに対し、上に書いた方法
では時刻
を直接計算できた。このように、直接計算できる
方法のことを陽解法 explicit method という。これに対し、上に書いた方法
では時刻 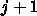 の項が右辺に複数現れているので、これは全体として
の項が右辺に複数現れているので、これは全体として
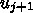 についての線形連立方程式になっている。このように、新しい時
刻での解が代数方程式を解かないと求められない方法のことを陰解法という。
についての線形連立方程式になっている。このように、新しい時
刻での解が代数方程式を解かないと求められない方法のことを陰解法という。
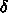 とか
とか 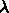 を定義す
ると、両者の関係が今度は
を定義す
ると、両者の関係が今度は

 なる任意の
なる任意の 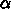 と
と 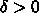 な
る任意の
な
る任意の 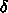 について、
について、  が満たされているのである。
つまり、どんなに
が満たされているのである。
つまり、どんなに 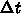 を大きくとっても、決して不安定にならない。
この性質を無条件安定という。この場合には、安定性ではなくて計算精度の観
点から
を大きくとっても、決して不安定にならない。
この性質を無条件安定という。この場合には、安定性ではなくて計算精度の観
点から 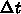 を決められることになり、だいぶましである。
を決められることになり、だいぶましである。
4.5. 3重対角行列を解く

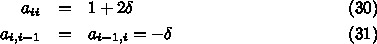
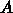 は
は 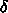 の符号が違うだけで前と同じ三重対角行
列になっている。行列(以下、線形連立方程式のことを単に行列ということ
がある)を解くのは例えばガウスの消去法では計算量が一般には次元の3乗に
なるので嬉しくないが、三重対角の場合には計算量が次元数に比例する。前進
消去で消さないといけない項が常に1つだけだからである。
の符号が違うだけで前と同じ三重対角行
列になっている。行列(以下、線形連立方程式のことを単に行列ということ
がある)を解くのは例えばガウスの消去法では計算量が一般には次元の3乗に
なるので嬉しくないが、三重対角の場合には計算量が次元数に比例する。前進
消去で消さないといけない項が常に1つだけだからである。
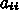 を ad,
を ad, 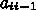 を al,
を al, 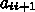 を ad、右辺の値を b と表して、前進消去の部分が、
を ad、右辺の値を b と表して、前進消去の部分が、
double c = al[i]/ad[i-1];
ad[i] -= c*au[i-1];
b[i] -= c*b[i-1];
というだけである。後退代入も、 au のところだけを消せばいいので
b[i] = (b[i]-au[i]*b[i+1])/ad[i];
というふうに一つ下の値を引くだけになる。
void solve_tridiagonal(double ad[],
double al[],
double au[],
double b[],
int n)
{
int i;
for(i=1;i<n;i++){
double c = al[i]/ad[i-1];
ad[i] -= c*au[i-1];
b[i] -= c*b[i-1];
}
b[n-1] /= ad[n-1];
for(i=n-2;i>=0;i--){
b[i] = (b[i]-au[i]*b[i+1])/ad[i];
}
}
となる。
void push_system(double u[],
double ad[],
double au[],
double al[],
int nx,
double dx,
double dt)
{
double delta = dt/(dx*dx);
int i;
for(i=0;i<nx-1;i++){
ad[i] = 1 + 2*delta;
al[i] = au[i] = -delta;
}
solve_tridiagonal(ad, al, au, u+1, nx-1);
}
である。
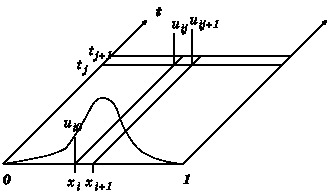
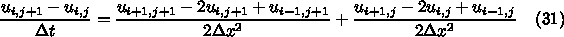
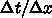 をいろいろ変えて安定に計算できることを確認せよ。
をいろいろ変えて安定に計算できることを確認せよ。
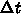 ,
, 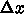 のそれぞれ何乗になっているか、
のそれぞれ何乗になっているか、 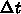 ,
, 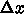 をいろいろ変えてプログラムを走ら
せて結果を厳密解と比べることで調べよ。厳密解と比べるには、初期条件がデ
ルタ関数では具合が良くないのでどういうものを使うべきか考えてみること。
をいろいろ変えてプログラムを走ら
せて結果を厳密解と比べることで調べよ。厳密解と比べるには、初期条件がデ
ルタ関数では具合が良くないのでどういうものを使うべきか考えてみること。
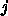 と
と 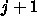 での空間微分の混ぜ方を変えているだけである。これらすべてを統一的に計算
できるプログラムを作成し、正しく動くことを確認せよ。
での空間微分の混ぜ方を変えているだけである。これらすべてを統一的に計算
できるプログラムを作成し、正しく動くことを確認せよ。