10. 最適化(2)
本章では、確率的最適化手法を扱う。
確率的な方法といってもいろいろあるが、現在応用や研究がさかんなのはシミュ レーテッドアニーリング(SA) と遺伝的アルゴリズム(GA) である。どちらも、 数学的な最適化手法というよりは、物理現象(SA)や生物の進化(GA)を真似する ことで、まあまあの解が得られたらうれしいなという方法である。で、 GA は この2つのなかでも新しい方法であり、理論的裏づけもいろいろはっきりしな いところがあるので、今日は主に SA の話をする。
アニーリングとは「焼きなまし」のことである。
理論的にはなにかを加熱したあと、ゆっくり冷や
すことで熱平衡状態を実現するということである。急に冷やすと熱平衡ではな
いところで固まってしまう。例えば、安定状態が結晶であるものでも、急速に
冷やすと欠陥が多い結晶になったり、あるいはアモルファスで固まったりする
わけである。
ここで、熱平衡状態というのは、熱力学的にはエネルギー最低の状態(何が最
低になっているかはもちろん境界条件、例えば圧力一定か体積一定かによる)
になっているわけで、つまり、世の中のあらゆる物質というのは、単に「ゆっ
くり温度を変える」というだけで、「エネルギー最低の状態を実現する」とい
う最適化問題を解いていることになる。特に、温度0での熱平衡状態は、系の
ポテンシャルエネルギーを最小化したものになっている。これを実
現するためには、系を熱平衡状態に保ちながらゆっくり冷やしていけばよい。
というわけで、そんな風にやろうというのが SA の基本的な考え方ということ
になる。
さて、熱平衡状態を実現しないといけないわけであるが、それにはどうすれば
いいだろうか?とりあえず、古典多粒子系の場合を例に考えてみる。
統計力学的には、温度・体積一定の系でのある物理量
ここで、ハミルトニアンが
これが実際に求められればある量
求めたいのは最適解とか最小値で平均でもなんでもないので、こんなの
が求まってもしょうがないのではと思うかもしれないけど、もうちょっと我慢
して欲しい。
ここで問題なのは、実際には上の積分は有限の計算量では評価できないという
ことである。実際の物理系では自由度がアボガドロ数くらいあるので全く論外
だが、例えば原子の数が100とか 1000 くらいにしたところでこれは 300 とか
3000 次元での数値積分になる。しかも、ほとんどのところでは出現確率
ここで、確率的積分というのを考えるわけである。確率的積分といっても、例
えばランダムに粒子をばらまいて、出現確率にしたがって重みをつけて積分し
ていっても、やはりほとんどのところで確率が非常に小さいのであまりうまく
いかない。確率が低くないところだけを重点的に拾うような方法が必要である。
これを実現するのがメトロポリス・モンテカルロ法というものである。ちなみ
にメトロポリスは人の名前で、ロスアラモス研究所の研究スタッフであった。
モンテカルロ法を提案した論文は1953年のもので、エドワード・テラー他4人
との共著論文である。ちょうど水爆を作っていたころの話である。
と、そんなことはさておき、メトロポリス法の大事なところは、全くランダム
に粒子をばらまくのではなく、今ある分布からちょっと変えてみてエネルギー
の変化をみて、それからどうするか決めるということである。
つまり、具体的には、以下のような手順で計算を進める
したがって、どのように動かすかというのは、上の対称性が成り立っているか
ぎりなんでもいいことになる。例えば、ある半径の球内の一様乱数でもいいし、
ガウシアンとか、もっと変なものでも構わない。計算の手間と収束性を考える
と、動かすのをあまり大きくするとほとんど採用されなくなって無駄であるし、
逆にあまり小さいと今度は時間をかけてもあまり配置が変わらないことになっ
てやはり無駄である。というわけで、採用される確率が 1/2 くらいになるよ
うにうまくとるのがいいということになっている。
さて、メトロポリス法はいいとして、それが最適化とどう関係するかという話
に戻る。メトロポリス法では、とにかくある温度でのアンサンブル平均を実行
できた。しかし、最適化によって我々がやりたいのは、ある関数の最小化であっ
て別に平均でもなんでもない。
ここで、温度
局所的な極小値に落ち込まないようにするには、最初は高い温度にしておいて、
ある程度位相空間全体を動けるようにしてメトロポリス法を適用し、それから
温度を下げてはまたメトロポリス法で動かすというのを繰り返すという方法が
考えられる。これが SA 法である。
実際上は、
さて、もともとのメトロポリス法では、原理として考えていたのは多粒子系の
熱平衡とかそういうもので、あんまり組合せ的最適化という感じはしない。
組合せ的最適化というと、代表的なのは前回にあげた巡回セールスマン問
題(TSP)のような、
つまり、 SA という観点からすれば、
TSP は、以下のようにかける。
巡回路自体は、
目的関数は、
定義域が連続的な関数とは違って、動かす量を調整することで採用確率を調整
するのは難しいというか、組合せ的最適化の場合にはそういうのを考えて
もしょうがない。
実際にプログラムを作る時には、定義式にしたがって目的関数を計算するので
はなく、つなぎ変えたことによる変化だけを計算すればいい。これによって一
回のモンテカルロ反復に対する計算量を
例えば、温度の変え方を指数型で
原理的には、近似解候補を与えた時に目的関数を計算する関数(手続き)と、
今の近似解からランダムに新しい近似解を作る手続きの2つがあればプログラ
ムは作れる。が、多くの場合に、「新しい近似解と今の近似解との差」を計算
するほうが計算量が減る。 TSP の場合であれば、これは
SA は、まあとにかく答がでるのが利点とはいえ、「ゆっくり冷やさないとい
けない」という条件がつくので計算量は多い。また、メトロポリス法では配置
を作っては乱数と比べるというのの繰り返しなので、普通にやったんでは並列
化して沢山計算機を使って速くするのも難しい。
最近、さまざまな並列化手法が提案されている。特に注目されているのは温度
並列 SA (TPSA) というもので、計算機毎に違う温度でモンテカルロをやり、
時々違う温度のもの同士を交換するという方法である。温度がもっとも低いも
ののところに最終的な結果が求まる。これは「レプリカ交換法」とかいろんな
名前がついているが、基本的な発想はみんな同じである。
TSP について、
参考プログラム
anneal.C を動かしてみて、単位正方形内にランダムに 100 個
程度の点をばらまいた時にどんな答がでるか見てみよ。また、アニーリングス
ケジュールをいろいろ変えてみて、答がどのように変わるか調べよ。
規則的に点を並べた場合には、TSP の厳密解が全数探索をしなくても求まる。
100点程度の場合にそのような厳密解がある場合を作ってみて、 SA で厳密解
に到達できるかどうか調べよ。
参考プログラムではコストがユークリッド距離であるとしている。これ
をマンハッタン距離(
10.1. シミュレーテッドアニーリングの考え
10.2. 熱平衡状態の実現 -- メトロポリス・モンテカルロ
 の値は、アンサンブル平
均によって与えられると考えられる。アンサンブル平均は、系のとりうるすべ
ての状態に対して、その出現確率で重みつけして平均をとる。
の値は、アンサンブル平
均によって与えられると考えられる。アンサンブル平均は、系のとりうるすべ
ての状態に対して、その出現確率で重みつけして平均をとる。
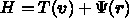 という風に位置の関数と速
度(運動量)の関数にわけられる(大抵そうである)場合を考えて、さらに求
めたい量が位置だけの関数である場合を考えると、速度については積分を落せ
るので以下の式がなりたつ。
という風に位置の関数と速
度(運動量)の関数にわけられる(大抵そうである)場合を考えて、さらに求
めたい量が位置だけの関数である場合を考えると、速度については積分を落せ
るので以下の式がなりたつ。
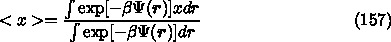
 が求まるということになる。ここで
が求まるということになる。ここで
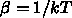 である。
である。
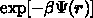 が非常に小さく、まじめに計算してもしょうがな
い。
が非常に小さく、まじめに計算してもしょうがな
い。
ここで、粒子を動かす向き、大きさが「適当」でもいいというのが大事なとこ
ろで、一般には、詳細釣り合いがなりたっていれば、つまり、相互に移動可能
な2つの状態
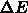 を計算する。
を計算する。
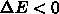 なら新しい配置を採用する。そうでなければ、確率
なら新しい配置を採用する。そうでなければ、確率 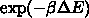 で新しい配置を採用する。
で新しい配置を採用する。
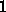 と
と  について、相互の遷移確率
について、相互の遷移確率 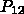 と
と 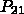 に以下の関係が
あれば
に以下の関係が
あれば
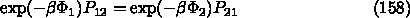
10.3. SA の実現
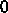 の極限を考えると、熱力学的にはもちろん温度
の極限を考えると、熱力学的にはもちろん温度 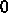 の極限
はポテンシャルエネルギーの極小値に対応する。が、温度
の極限
はポテンシャルエネルギーの極小値に対応する。が、温度 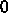 で機械的にメ
トロポリス法をやってもうまくいくとは限らない。というのは、温度
で機械的にメ
トロポリス法をやってもうまくいくとは限らない。というのは、温度 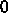 は
は
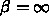 に対応し、少しでもエネルギーが増えるような移動はしな
いということに対応する。したがって、計算を始めたところの近くに局所的な
極小値があれば、そこに落ち込んで計算が止まってしまうからである。
に対応し、少しでもエネルギーが増えるような移動はしな
いということに対応する。したがって、計算を始めたところの近くに局所的な
極小値があれば、そこに落ち込んで計算が止まってしまうからである。
といったことを考えないといけない。この辺は理論がないわけではないが、そ
れは例えば収束性を保証するためには温度は 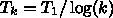 というふ
うに繰り返し数
というふ
うに繰り返し数 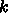 の対数でしか温度を下げられないというようなものなの
であまり役に立たない。実際には、
の対数でしか温度を下げられないというようなものなの
であまり役に立たない。実際には、 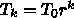 という風に指数関数的
に温度を下げても意外にうまくいってしまう。そういうわけで、実際に問題を
持ってきた時に上のようなパラメータ(総称してアニーリング・スケジュール
ということが多い)をどう決めるかは、いろいろ実験してみる必要がある。
という風に指数関数的
に温度を下げても意外にうまくいってしまう。そういうわけで、実際に問題を
持ってきた時に上のようなパラメータ(総称してアニーリング・スケジュール
ということが多い)をどう決めるかは、いろいろ実験してみる必要がある。
10.4. 組合せ的最適化への SA の応用
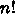 個の組合せを調べあげないと答がわからないようなもので
ある。この他にも、ナップザック問題とか最大充足問題とかいろんなものがあ
るが、 SA を使うという観点からすればどれも同じようなものである。
個の組合せを調べあげないと答がわからないようなもので
ある。この他にも、ナップザック問題とか最大充足問題とかいろんなものがあ
るが、 SA を使うという観点からすればどれも同じようなものである。
の2つを与えることができれば、あとはアニーリング・スケジュールを決めれ
ば答がでる。さらに、前に述べた議論から、近くの解を発生する方法は、対称
性さえ満たしていれば適当でいい。収束の速さとかを考えると適当にするより
いろいろ考えた方がいいのは当然だが、それは収束の速さに影響するだけだし
その影響もあまり大きくないのが SA のいいところである。これは、条件が悪
いと実際上収束しなくなる最急降下法なんかとはだいぶ違う。
10.4.1. SA でTSPの近似解を求める
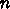 個の点
個の点  に対して、点間の移動コスト
に対して、点間の移動コスト 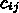 が与えら
れているとする。
が与えら
れているとする。 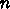 個の点をすべて通ってもとに戻るような巡回路でコス
トの合計が最小になるようなものを見い出せ。
個の点をすべて通ってもとに戻るような巡回路でコス
トの合計が最小になるようなものを見い出せ。
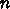 個の点(の番号)の並び
個の点(の番号)の並び  で与えられる。
この並びは 1 から
で与えられる。
この並びは 1 から 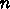 までを並べ変えたもの、つまり、ここで <$1\ge q_i
\ge n, \quad q_i \ne q_j (i\ne j)$>ということになる。
までを並べ変えたもの、つまり、ここで <$1\ge q_i
\ge n, \quad q_i \ne q_j (i\ne j)$>ということになる。

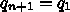 とする)であるので簡単に計算できる。近くの解
の発生のさせ方だが、もっとも簡単なのは
とする)であるので簡単に計算できる。近くの解
の発生のさせ方だが、もっとも簡単なのは 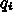 と
と 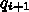 を入れ換えて
みるというものである。もっと大きくつなぎ変えたければ、適当に2箇所を選
んでそこで切ってひっくり返してつなぐというのも考えられる。こちらのほう
が、局所的な最適解に落ちる可能性が少ないという意味では安全である。
を入れ換えて
みるというものである。もっと大きくつなぎ変えたければ、適当に2箇所を選
んでそこで切ってひっくり返してつなぐというのも考えられる。こちらのほう
が、局所的な最適解に落ちる可能性が少ないという意味では安全である。
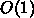 にすることができる。
にすることができる。
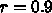 とし、一温度での反復は
とし、一温度での反復は  とか、採用されたのが
とか、採用されたのが 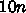 とか適当に決めて、大抵の場合にちゃんとした
答がでるようである。
とか適当に決めて、大抵の場合にちゃんとした
答がでるようである。
10.4.2. SA のプログラムの一般的な方針
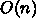 と
と 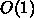 で非常に大きい。また、古典粒子系のモンテカルロのように目的関数が全粒子間のポテン
シャルエネルギーの和であれば、全部計算すれば
で非常に大きい。また、古典粒子系のモンテカルロのように目的関数が全粒子間のポテン
シャルエネルギーの和であれば、全部計算すれば 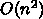 だが動かしたこと
による変化は
だが動かしたこと
による変化は 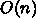 である。このように、変化分を高速に計算する方法を工
夫することが極めて重要になる。
である。このように、変化分を高速に計算する方法を工
夫することが極めて重要になる。
10.4.3. もっと高速化する方法
10.5. 練習
10.5.1. 問題 1
10.5.2. 問題 2
10.5.3. 問題 3
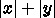 )にして、答の変化を見てみよ
)にして、答の変化を見てみよ
10.5.4. 問題 4
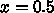 のところに川があって、川を渡るのには
のところに川があって、川を渡るのには 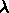 のコストが余計に掛かるとして答の変化を見てみよ。もっともらしいか?また、
どのようにしてもっともらしいと判断したか?
のコストが余計に掛かるとして答の変化を見てみよ。もっともらしいか?また、
どのようにしてもっともらしいと判断したか?
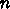 個の円を重ならないように詰め込めるような
円の最大半径はいくつか」という問題を、「円の詰め込み問題」という。いく
つかの
個の円を重ならないように詰め込めるような
円の最大半径はいくつか」という問題を、「円の詰め込み問題」という。いく
つかの 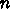 については厳密解が知られているが、一般の
については厳密解が知られているが、一般の 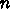 について解かれ
ているわけではない。これを SA で解いてみて、どれくらいもっともらしい答
がでるか調べよ。目的関数として、
について解かれ
ているわけではない。これを SA で解いてみて、どれくらいもっともらしい答
がでるか調べよ。目的関数として、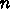 個の点間の距離と壁への距
離の最小値をとればよい。知られている厳密解のいくつかはまとめられ
ているので、比べてみること。
個の点間の距離と壁への距
離の最小値をとればよい。知られている厳密解のいくつかはまとめられ
ているので、比べてみること。