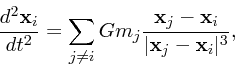 |
(1) |
牧野淳一郎
この講義では、天体物理学の扱う主要な対象の一つである自己重力多体系の進 化とその理解について、その概要を扱うことにしたい。
「自己重力多体系」というと、難しそうに聞こえるが、基本的には「たくさん の質点が重力で引き合って、まとまった天体を作っている」というものである。 例えば方程式で書けばすべての粒子が他のすべての粒子からの重力を受けて運 動するというだけのことである。
しかし、実際に宇宙にある自己重力多体系を見ると、非常に多様な進化を遂げ ているということはすぐにわかる。この多様性がもっとも顕著なのは銀河であ り、基本的には重力で星が集まっているだけなのに、円盤(渦巻)銀河、棒渦 巻銀河、楕円銀河、あるいは不規則銀河などじつに多様な形をしたものがある。 また、最近の特に HST による High-Z の観測から、このような銀河の形は進 化してきたものである、例えば昔に遡って見ると「晩期型」銀河のほうが「早 期型」銀河より多い(方向が逆だけど、これは定義の問題)ということがわかっ てきた。
これに対し、例えば「球状星団」と呼ばれる銀河内の星団は、比較的単純な 丸い形をしていて、回転もほとんどしていない。また、半径方向の光度分布に ついても共通の特徴がある。
さらに小さいスケールで、惑星系を考えると、20年くらい前までは惑星系とい うと我々の太陽系しか知られていなかったので、多様かどうかも良くわかって いなかったが、系外惑星が見つかってくると極めて多様であることがわかって きた。
ここで銀河と惑星系には、「どちらもほぼ円盤である」という共通性があり、 これはもちろん、どちらもガス雲が収縮していく過程でできたもので、初めか ら質点系であったわけではないからである。つまり、自己重力的なガスには またそれなりの共通な性質がある。
逆に大きいスケールに移って、銀河群、銀河団といったものを考えると、これ らは(銀河の数が少ないこともあるが)良くわからない形をしているものが多 い。結構丸くまとまっているものもあるが、縦に伸びたもの、二つの銀河団が お互いの回りを回っているものなど、多様な銀河団がある。また、比較的大き な銀河団のなかには、 cD と呼ばれる異常に大きな楕円(ほとんど球に近い) 銀河を持つものが多い。
さらに、ここ 30 年ほどの、大規模な銀河分布についての研究から、宇宙には 銀河、あるいは銀河団が一様に分布しているわけでは全くなく、大きなスケー ルで構造があるということがわかっている。
以上のようなさまざまな現象は、「重力多体系」という描像で(基本的に は)統一的に理解することができる。その統一的な描像の概要を与えるのがこ の講義の目標ということになる。
具体的には以下のようなトピック を扱う。
(ここまだ変えるかも)
まず、無衝突ボルツマン方程式を導いてその 振舞いについて少し考える。無衝突ボルツマン方程式は、 恒星系力学の基礎方程式といえる。
原理的には、恒星系力学の基礎方程式は何かというと、恒星系は自己重力多体系 と考えていいわけで、各粒子(恒星)の運動方程式
が基礎方程式ということになる。
数値計算にはもちろんこれを使うわけだが、理論的な扱いには不便である。
というわけで、しばらくは(1粒子)分布関数
![]() で話をする。
ここでは、粒子数が「無限に大きい」と思って、6次元の位相空間
で話をする。
ここでは、粒子数が「無限に大きい」と思って、6次元の位相空間
![]() の中の粒子の密度分布の時間進化を考える。
この時の基礎方程式が(無衝突)ボルツマン方程式である。
の中の粒子の密度分布の時間進化を考える。
この時の基礎方程式が(無衝突)ボルツマン方程式である。
以下、方程式を導く。位相空間での座標を
![]() と書くこと
にする。また、重力ポテンシャルを
と書くこと
にする。また、重力ポテンシャルを
![]() とおくと、位相空間
の中での粒子の流れは
とおくと、位相空間
の中での粒子の流れは
| (2) |
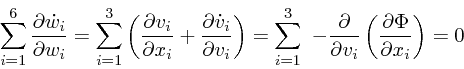 |
(4) |
| (6) |
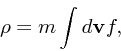 |
(7) |
なお、以下の議論では(当分) ![]() のことは忘れて、その代わり
のことは忘れて、その代わり ![]() が個数
密度ではなくて質量分布であるということにしておく。
が個数
密度ではなくて質量分布であるということにしておく。
直観的な意味は
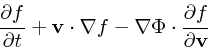
これらから、まず、「力学平衡状態」とはどう定義され、どういう性 質があるかということを考え、それから具体的な平衡状態の例を見ていくこと にする。
まず、「力学平衡」とは何かということだが、これは、上の無衝突ボルツマン
方程式とポアソン方程式を連立させたものの定常解、すなわち、時間的に変化
しない解ということになる。従って、ある分布関数 ![]() が力学平衡にあると
いうことは、それによって決まるポテンシャル
が力学平衡にあると
いうことは、それによって決まるポテンシャル ![]() を固定して考えた時に、
を固定して考えた時に、
![]() の時間微分が
の時間微分が ![]() になるということである。
になるということである。
直観的には、粒子数が無限に多い重力多体系で、時間がたっても 形が変わらない、というのが力学平衡にある、ということである。
これは楕円銀河とかは実際にそういう状態にあるが、どうやってそういう状態 が可能になっているかはちゃんと理解するのは意外に面倒である。以下、 簡単な場合から考えていく。
ここで、わざわざ「力学」とつけるのは、もちろん平衡状態にはほかにもいろ いろあるからである。もっとも重要なのは熱平衡の概念であるが、これはまた 後で。
あと、平衡状態だけ考えでもしょうがなくて、私達は系がどう進化するかを理 解したかったのでは?という疑問は当然あると思うが、これは
というようなことで、、、
平衡状態というものを考える上で基本になるのは、「運動の積分」という概念
である。ポテンシャル ![]() のもとで、ある
のもとで、ある
![]() の関数
の関数 ![]() が運動
の積分であるとは、その上で
が運動
の積分であるとは、その上で
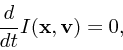 |
(8) |
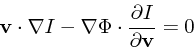 |
(9) |
なお、「運動の積分」というときの流儀は2通りあって、一般に運動の保存量 のことを「運動の積分」という流儀もあるが、ここでは位相空間の座標だけの関数 であって同時に保存量であるものをさす。具体的には、たとえば1次元調和振 動子で「初期の位相」というのは保存量だが運動の積分ではない。これは、時 間が入ってくるからである。
エネルギー ![]() や、ポテンシャルが球対称(
や、ポテンシャルが球対称(![]() だけの関数)の
場合の角運動量ベクトル
だけの関数)の
場合の角運動量ベクトル
![]() は運動の積分である。
は運動の積分である。
さて、上のように ![]() を定義すると、以下の「ジーンズの定理」がなり立つ
ことがわかる。
を定義すると、以下の「ジーンズの定理」がなり立つ
ことがわかる。
ジーンズの定理 任意の無衝突ボルツマン方程式の定常解は、運動の積 分を通してのみ位相空間座標に依存する。逆に、任意の運動の積分の関数は定 常解を与える。
いいかえると、分布関数 ![]() が定常であるためには、運動の積分
が定常であるためには、運動の積分
![]() があって
があって
![]() の形で書けることが必
要十分ということ。
の形で書けることが必
要十分ということ。
証明だが、まず「定常ならば運動の積分で書ける」というほうを考えてみる。こ
れは、![]() 自体が運動の積分の定義を満たしているので、 OK。
自体が運動の積分の定義を満たしているので、 OK。
逆のほうは、実際に ![]() の全微分を
の全微分を![]() で書き下せば、それぞれが 0 にな
るということからいえる。
で書き下せば、それぞれが 0 にな
るということからいえる。
というわけで、これはなかなか強力な定理だが、一般の場合にはそれほど役に 立つわけではない。というのは、ポテンシャルを与えた時に一般に運動の積分 というのは 5 個あるはずだが、それらをすべて知っているということはない からである。
ただし、球対称とか軸対称とか条件をつけると、いろいろちゃんと決まるよう になる。以下、まず球対称の場合を考える。
球対称ではない場合については後でもう一度。
球対称の場合、運動の積分はエネルギーと角運動量の3成分で4つある。一般に はもう一つあるが、これは特別な場合を除いてあまり意味がないので、定常な 分布関数はエネルギーと角運動量だけで書けると思っていい。
いちおう、ここで、意味がないというのはどういうことかということを説明し ておく。そのためには、意味がある特別な場合というのを考えるのがよい。こ れは、ケプラー軌道のような、軌道が閉じる場合である。この時には、エネル ギーと角運動量の他に、軌道全体の向きを表す量(近点経度)が保存する。こ れはちゃんと保存量になっている。
しかし、一般には軌道が閉じない。このときでも、近点経度に対応するような 保存量が実は存在しているが、それにも関わらず、ある軌道がエネルギーと角 運動量で決まる部分空間を覆ってしまう(数学的には、もちろんすべての点を 覆えるのではなく、任意の点について、いくらでも近くにいけるというだけだ が)。こうなっていると、その積分に分布関数が依存すると、連続性とか微分 可能性とかに困難を生じることになる。
さて、 ![]() は
は ![]() と
と ![]() によるということにしたわけだが、いま球
対称な場合ということなので
によるということにしたわけだが、いま球
対称な場合ということなので ![]() の方向にではなく、絶対値だけに依
存するのでないといけない。したがって、実は球対称の分布関数は一般に
の方向にではなく、絶対値だけに依
存するのでないといけない。したがって、実は球対称の分布関数は一般に
![]() と書けるということになる。
と書けるということになる。
我々が扱いたいのは自己重力系なので、実際にこれを球対称の場合に書き下し てみると
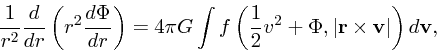 |
(10) |
上の場合でもまだちょっと大変なので、さらに単純化してとりあえず ![]() に
もよらない場合というのを考えてみる。これには、なかなか特別な、
空間上の各点で速度分散が等方的であるという性質がある。これはどういうこ
とかというと、一般にある方向の速度分散というのは
に
もよらない場合というのを考えてみる。これには、なかなか特別な、
空間上の各点で速度分散が等方的であるという性質がある。これはどういうこ
とかというと、一般にある方向の速度分散というのは
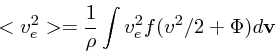 |
(11) |
以下、扱いやすくするために変数をとり直す。
| (12) |
これらを使って、さらに![]() の角度方向に渡って積分すれば
の角度方向に渡って積分すれば
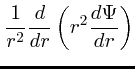 |
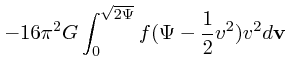 |
||
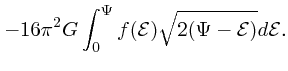 |
(13) |
これで、一般に ![]() を与えて
を与えて ![]() を求めるとか、あるいはその逆とかが
出来る。
を求めるとか、あるいはその逆とかが
出来る。
ただし、 ![]() を与えて
を与えて ![]() を求めようってときには、求まった
を求めようってときには、求まった ![]() が
が
![]() の条件を満たすという保証はないので、そういうのは物理的には意
味がない解ということになる。
の条件を満たすという保証はないので、そういうのは物理的には意
味がない解ということになる。
ここであげるのはあくまでも例であるが、さまざまな理由からその性質がよく 調べられているものである。
ある意味でもっとも簡単な分布関数の例は、 ![]() の冪乗(パワー)で書け
るものである。例えば
の冪乗(パワー)で書け
るものである。例えば
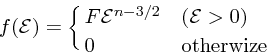 |
(14) |
| (15) |
上を使ってポアソン方程式から ![]() を消去すると
を消去すると
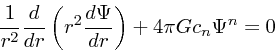 |
(16) |
変数を適当にスケーリングして
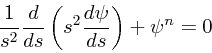 |
(17) |
実際には、上の Lane-Emden 方程式を解かないとポテンシャルや密度がどうなっ
ているかはよくわからない。で、一般の ![]() ではこの方程式には初等的な解
はないが、
ではこの方程式には初等的な解
はないが、 ![]() の場合には解があることが古くから知られている。これは
の場合には解があることが古くから知られている。これは
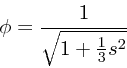 |
(18) |
密度が ![]() で有限で、
で有限で、
![]() で
で ![]() より速く落ちる
ので、質量は有限である。
より速く落ちる
ので、質量は有限である。
これは、天文学的になにか素晴らしいものであるというわけではないが、球状星 団のうち中心密度が低いものにはまあまあ似ていなくもない。とりあえず、こ れの意味は、解析関数で簡単に書ける自己重力系の self-consistent なモデ ルであるということである。
プラマーモデルは、いろんなシミュレーションの初期条件として使われること が多い。
プラマーモデルはその存在が100年くらい前から知られているが、こちらは論文が発表
されたのが 1990 年(というわけで、 Binney & Tremaine のときにはまだ知
られていなかった)という、非常に新しいモデルである(Hernquist, L.,
1990, ApJ 356, 359)。これは、ポテンシャルを
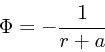 |
(19) |
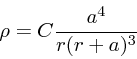 |
(20) |
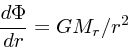 |
(21) |
Hernquist Model には、「![]() 則をかなり良く再現する」という著しい特
徴がある。
則をかなり良く再現する」という著しい特
徴がある。
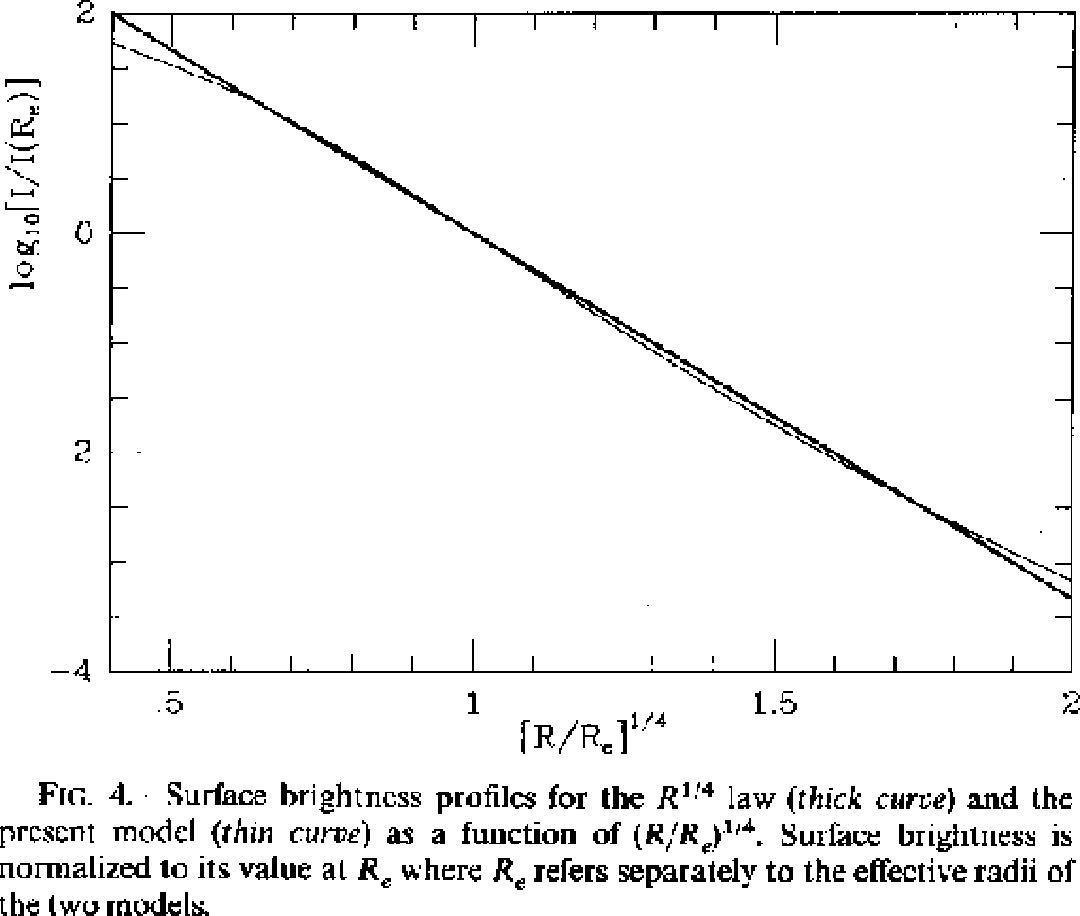
![]() 則については後でその物理的解釈も含めて詳しく議論することにし
たいが、要するに、観測される楕円銀河の表面輝度の対数(要するに等級です
ね)が、半径の
則については後でその物理的解釈も含めて詳しく議論することにし
たいが、要するに、観測される楕円銀河の表面輝度の対数(要するに等級です
ね)が、半径の![]() 乗に対して直線にのって見えるというものである。この
性質と、一応解析関数で分布関数が書けるということのために、楕円銀河やダー
クハローのモデルとして広く使われるようになってきている。
乗に対して直線にのって見えるというものである。この
性質と、一応解析関数で分布関数が書けるということのために、楕円銀河やダー
クハローのモデルとして広く使われるようになってきている。
ただし、このモデルにはいくつか妙な性質もあり、それについてもまた後で触 れることになるはずである。
前回、無衝突ボルツマン方程式の定常解は熱平衡とは限らないし、そもそもエ
ントロピーが発生しないのだから系が熱平衡に向かって進化するとも限らない
という話をした。が、後で出てくるようないくつかの理由から、熱平衡状態に
ついて良く理解しておくことは結構大事である。
熱平衡状態では(古典統計なので)分布関数はマックスウェル-ボルツマン分
布、すなわち
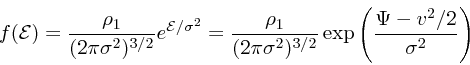 |
(22) |
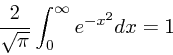 |
(23) |
| (24) |
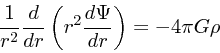 |
(25) |
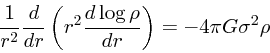 |
(26) |
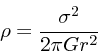 |
(27) |
特に、渦巻銀河については、「回転速度が中心からの距離に(あまり)依存し
ない」(いわゆる flat rotation curve)という性質が知られていて、これを
説明するためには上のような
![]() のダークハローが必要である
ということになっている。
のダークハローが必要である
ということになっている。
特別ではない解は、中心密度を有限にして中心から外側に向かって解いていけ
ばいい。この時でも、
![]() の極限では singular
isothermal に近付く。
の極限では singular
isothermal に近付く。
等温モデルは、エントロピー極大であり、分布関数がボルツマン分布になって
いるという特別な性質がある。このため、等温ガス球と実は同じ構造をとる。
以下、ガス球について方程式を導いておく。
静水圧平衡の式は
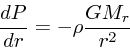 |
(28) |
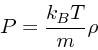 |
(29) |
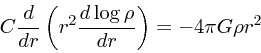 |
(30) |
なお、ポリトロープでも、ポリトロピックな状態方程式を持つガス球の密度分 布と stellar system のそれとは一致する。が、等温モデルの場合とは実は本 質的な違いがある。等温モデルの場合は、分布関数そのものが一致する(ボル ツマン分布であり、局所的にも大局的にもエントロピー最大)が、一般のポリ トロープではそんなことはない(そもそもガス球ではジーンズの定理が成り立 たないし、局所的にはボルツマン分布であるから)。
球対称ではない場合の例として、まず軸対称の場合を考える。
この場合、運動の積分として確実に存在するのはエネルギーと、対称軸回りの 角運動量だけである。但し、では他に運動の積分はないのかというと、話は既 に簡単ではなくなる。これは以下のように理解できる。
軸対称ポテンシャルなので、座標を ![]() ) の円筒座標にしてみる。
) の円筒座標にしてみる。
![]() を決めると角運動量保存から
を決めると角運動量保存から ![]() が決まるので、こちらは解く
必要がなく、
が決まるので、こちらは解く
必要がなく、 ![]() 平面の中の運動を考えればよい。そうすると自由度が
2なので、運動の積分がエネルギーの他にもうひとつあると可積分になって、
「解析的に解ける」。
平面の中の運動を考えればよい。そうすると自由度が
2なので、運動の積分がエネルギーの他にもうひとつあると可積分になって、
「解析的に解ける」。
例えば、 ![]() 平面内の運動にした後で、ポテンシャルが
平面内の運動にした後で、ポテンシャルが
| (31) |
ところが、調和振動子に少し余計な項を加えると、もうよくわからないことが 起こる。この有名な例が Hénon-Heiles (エノン-ハイレス)系である。 Hénon も Heiles も天文学者であり、この系は元々円盤銀河のような 軸対称ポテンシャルの中での恒星の運動のモデル方程式として導かれたもの である。
Hénon と Heiles (1964 AJ 69, 73) は、 ![]() として以下のようなものを考
えてみた。
として以下のようなものを考
えてみた。
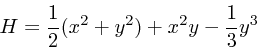 |
(32) |
何故この形を考えたかというのは、論文には以下のように書いてある
because: (1) it is analytically simple; this makes the computation of the trajectory easy; (2) at the same time, it is sufficiently complicated to give trajectories which are far from trivial, as will be seen below.
つまり、物理的あるいは天文学的になにかの意味があるというよりは、このポ テンシャルの中での軌道の振る舞いが妙であるということで選ばれたかなり人 工的な例ではある。
もちろん、最初の項は調和振動であり明確な意味がある。非線型の第2項の意 味はポテンシャルの等高線を書いて見ると分かる。
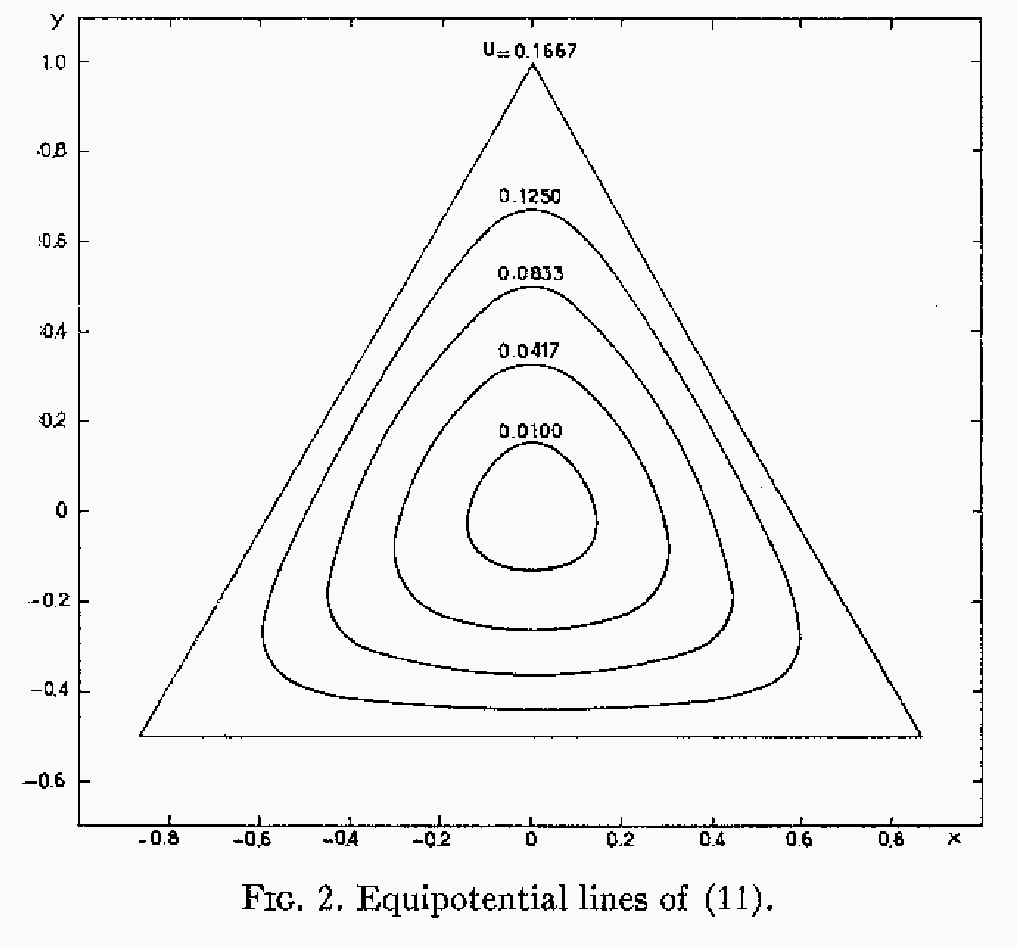
このように、非線型項によりポテンシャルが三角形になっている。特に
![]() の等高線に注意すると、これは直線になっている。このことから、こ
の三角形の頂点はポテンシャルの鞍点であり、力が 0 になることが分かる。
の等高線に注意すると、これは直線になっている。このことから、こ
の三角形の頂点はポテンシャルの鞍点であり、力が 0 になることが分かる。
鞍点であるので、ポテンシャルが下がるのは三角形の内側を向いた方向とその 反対側の方向だけであり、それに直交する方向ではポテンシャルは増えている。 また、頂点以外では力は 0 でない。
軌道は例えばこんなふうである。これはエネルギー(ハミルトニアン)
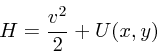 |
(33) |
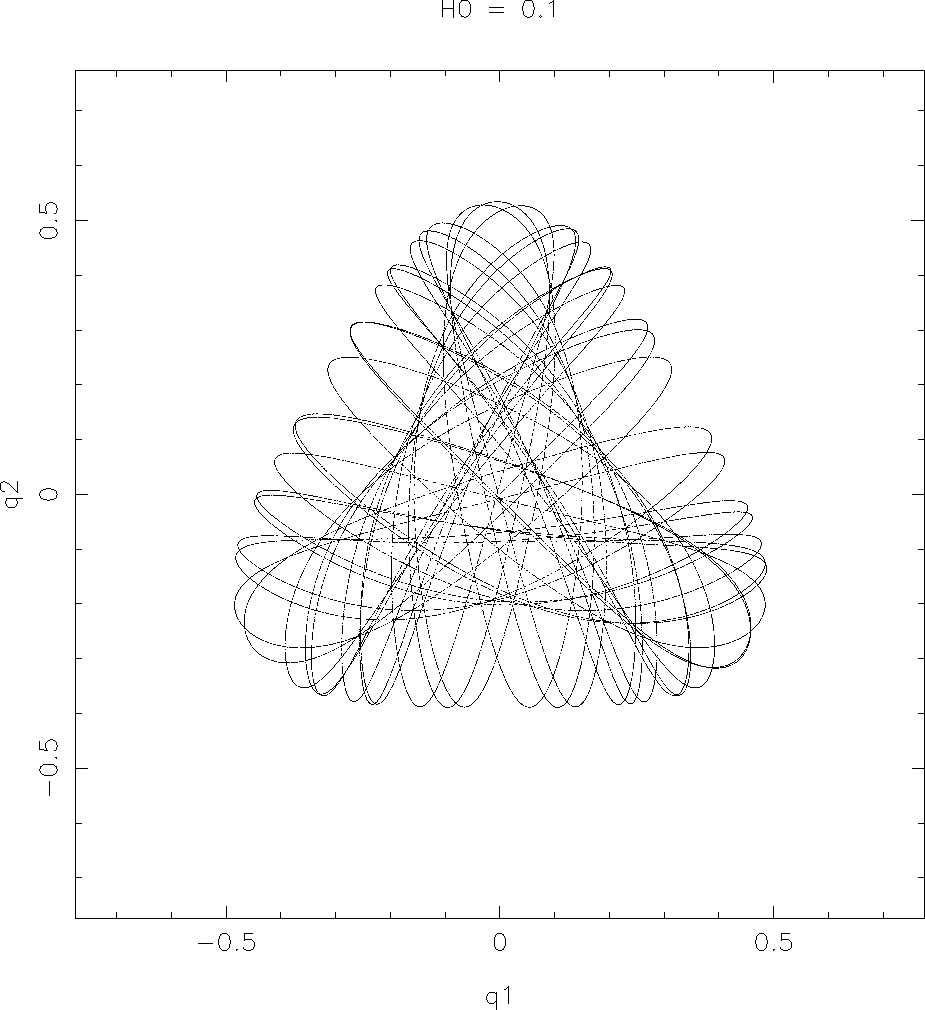
これだけを見ていると別にどうということはないが、ここでいわゆるポアンカ
レ断面というものを書いて見ると非常に面白いことになっていると分かる。ポ
アンカレ断面とは、 この場合のような自由度が2のハミルトン力学系で、一方
の変数、例えば ![]() が 0 になる時に
が 0 になる時に ![]() ,
, ![]() の値を書いたものである。
の値を書いたものである。
まず、 ![]() の場合を示す。
の場合を示す。
8cm
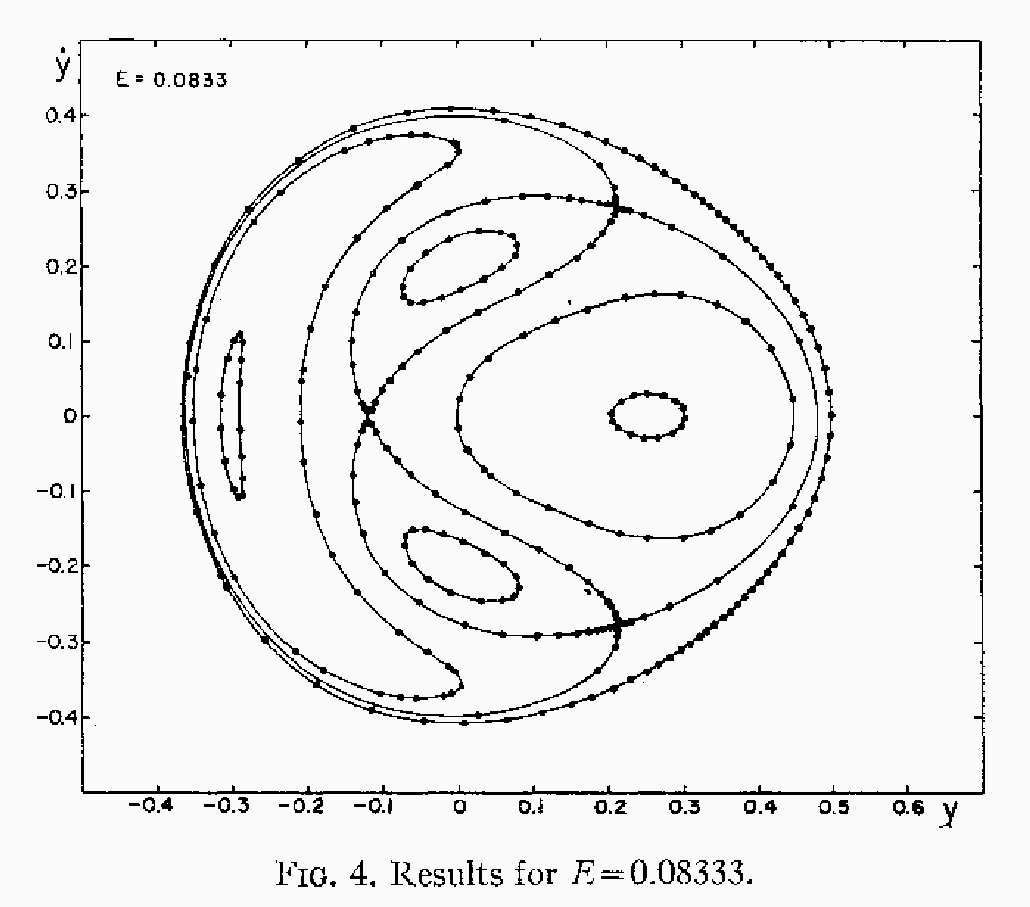
ここで、つながって線になっているのは基本的には一つの軌道であり、分かれ
た曲線は別の初期条件からの軌道に対応している。エネルギー保存を考えると、
![]() で
で ![]() なので、
なので、 ![]() ) はある閉領域の中にくる。保存
量がエネルギーだけであれば、任意の初期条件から出発した軌道はこの領域の
全ての点をいつかは通ると考えられるが、 このようにそうならないというこ
とは、なんだかわからない保存量のようなものがあるということを示している。
元々の軸対称ポテンシャルに戻ると軸回り角運動量は保存しているが、これは
有効ポテンシャルにして回転方向の速度を消去するのに使っているので、2次
元問題になった後では無関係である。
) はある閉領域の中にくる。保存
量がエネルギーだけであれば、任意の初期条件から出発した軌道はこの領域の
全ての点をいつかは通ると考えられるが、 このようにそうならないというこ
とは、なんだかわからない保存量のようなものがあるということを示している。
元々の軸対称ポテンシャルに戻ると軸回り角運動量は保存しているが、これは
有効ポテンシャルにして回転方向の速度を消去するのに使っているので、2次
元問題になった後では無関係である。
軸対称ポテンシャル内での運動にエネルギーと角運動量以外の保存量があるか どうかという問題は、「第3積分問題」と呼ばれる恒星系力学上の現在でも完 全には解決されているとはいいがたい問題の一つである。 とりあえずこの場 合には、第3積分が存在しているように見える。
但し、妙なのは、ポアンカレ断面上の軌跡が交点をもつように見えることであ る。実際には、この「交点」のところを精密に調べると、奇妙なことがわかる。 交点近くの十分に狭い領域では運動の積分が無くなって、ある領域内を軌道が 埋めているのである。
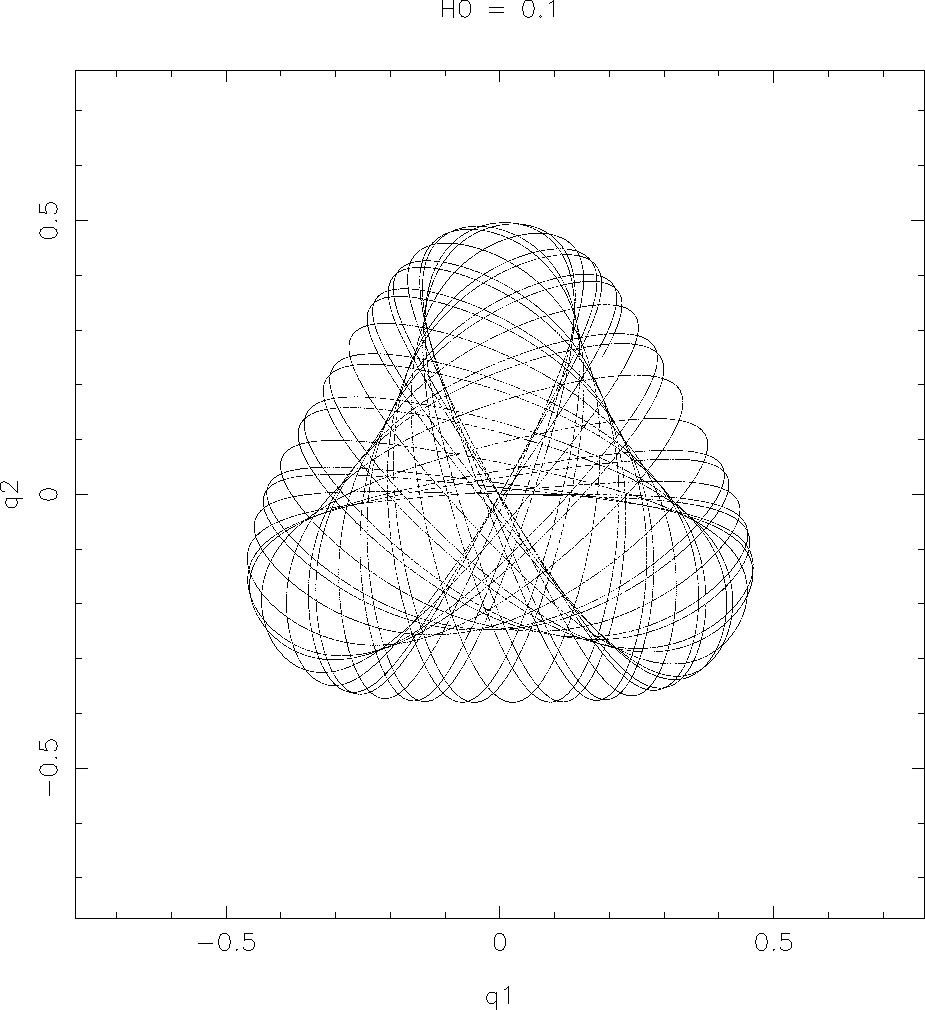
この領域はエネルギーを大きくするとどんどん大きくなる。次は ![]() の場合である。
の場合である。
8cm
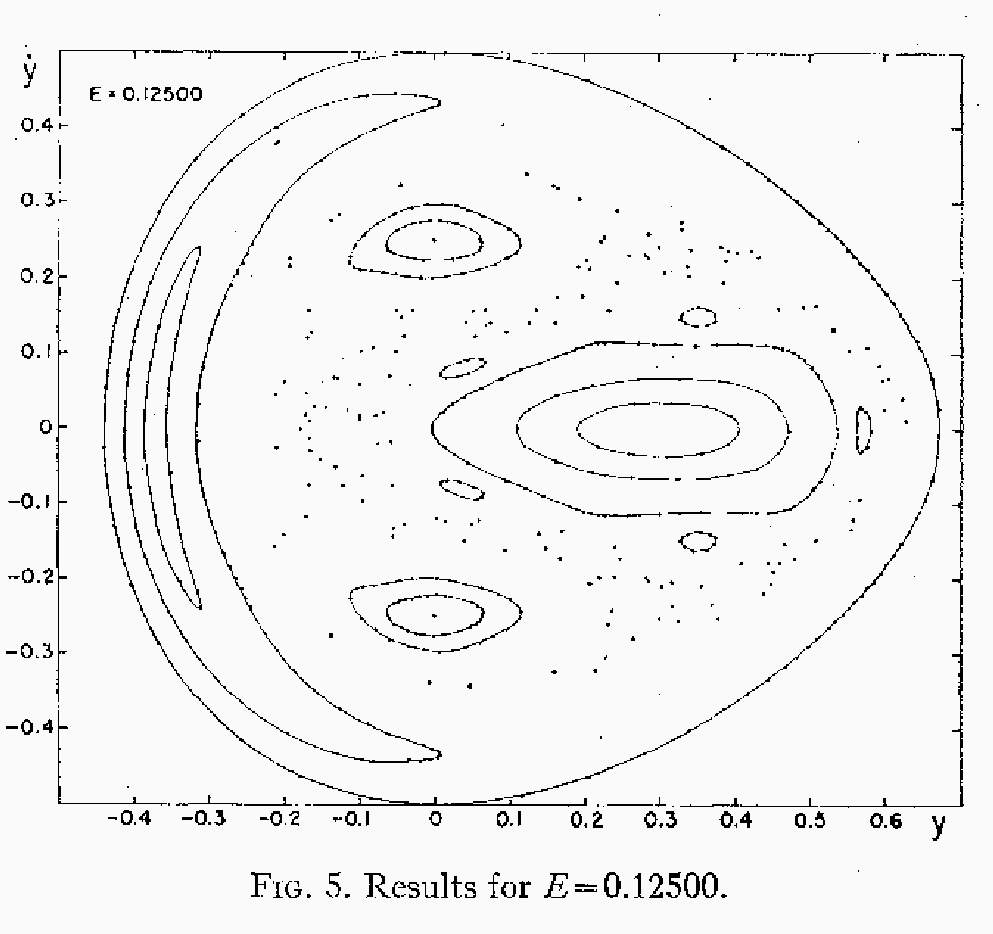
保存量を持つ、規則的な運動をする領域よりも、規則的ではない運動をする領 域のほうが広くなってしまっていることが分かる。少なくとも恒星系力学では、 このような場合に 規則的な軌道を regular orbit, そうでないものを irregular orbit または chaotic orbit という。
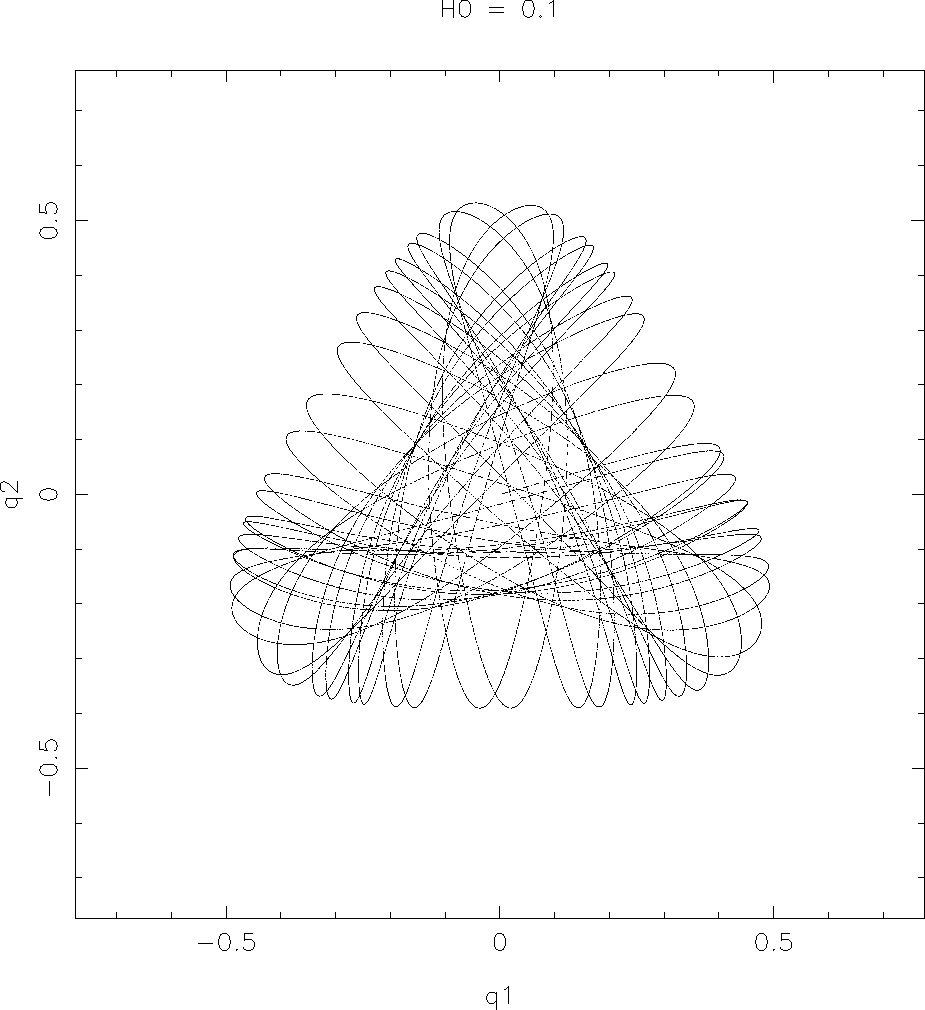
さらにエネルギーの上限に近い
![]() をとったものが下である。
をとったものが下である。
8cm
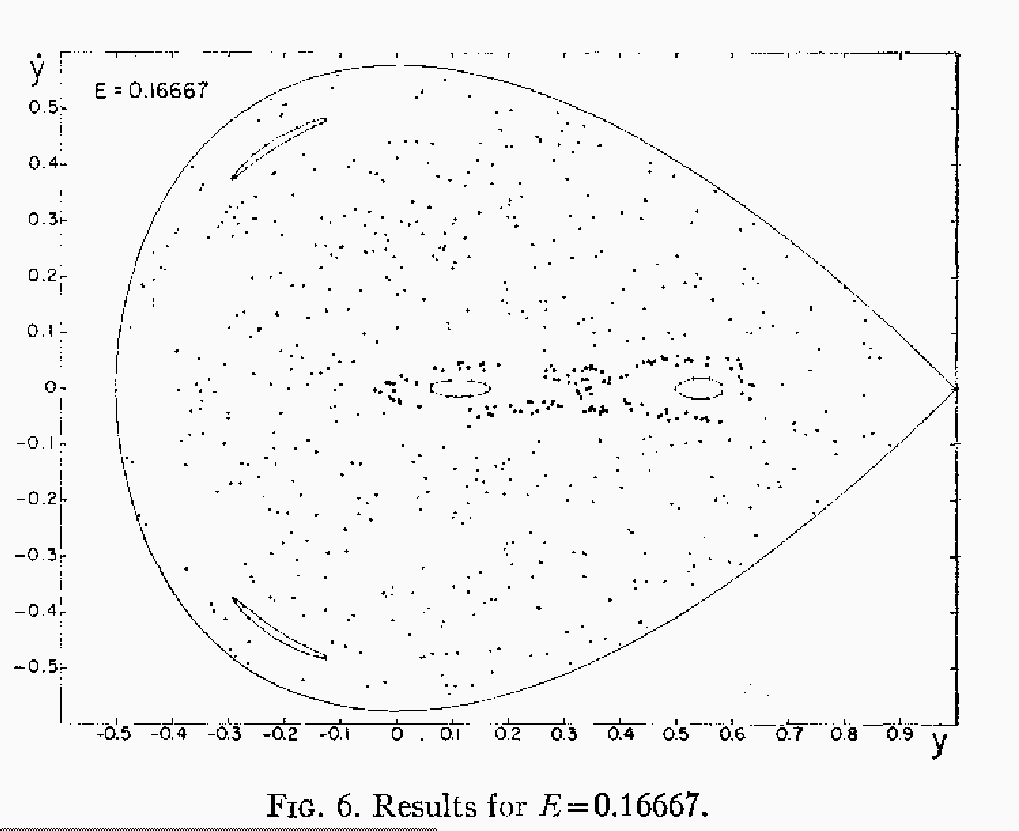
キャプションには ![]() よりも大きいようなことが書いてあるが、気の迷い
であろう。それはともかく、この場合にはほとんどの領域が規則的でない、つ
まり、第3積分をもたないような軌道になっていることが分かる。
よりも大きいようなことが書いてあるが、気の迷い
であろう。それはともかく、この場合にはほとんどの領域が規則的でない、つ
まり、第3積分をもたないような軌道になっていることが分かる。
これはカオス的な運動の典型的な例である。
ここではカオスかどうかを、エネルギー以外の積分がある(ように見える)かど うかで判断したが、実質的に同じことになるもうひとつの定義がある。それは、 「十分に近い初期条件から出発した2つの軌道がどのように離れていくか」で ある。より厳密にはこれはリヤプノフ指数が正かどうかということになる。定 義の詳細はここでは省くが、大雑把にはリヤプノフ指数が正なら十分近い2つ の軌道が指数関数的に離れていく。このことは上の Hénon-Heiles 系でも観 察され、周期的に見える領域では軌道は時間の1次で離れていくが、カオス的 な領域では指数関数的に離れる。
というわけで、軸対称でも話は球対称の場合よりはるかに難しくなる。実際に 理論的に軸対称な系、例えば楕円銀河とか回転がある球状星団とかを扱う時に は第三積分はないものとしてジーンズの定理を使って分布関数を構成すること はできるが、実際には多くの場合に第三積分的なものはあるのでそれ以外の解 がないというわけではない。
なお、2次元円盤の場合は話が簡単で、全ての軌道は可積分である。なので、 薄い円盤の場合にはほぼ可積分として扱うことができる。
多くの楕円銀河は実は軸対称でもなく、楕円の3軸の長さが全て違う。 そうすると、角運動量の3成分が全て保存しなくなり、自明な保存量は エネルギーだけになる。
しかし実際にはその中で regular orbit と呼ばれる、エネルギー以外の保存 量を持つ軌道があり、それによって3軸不等な形状を維持していると考えられ ている。
というわけで、今回の講義では球対称な系を中心に扱う。後半では円盤の話も する。
この文書はLaTeX2HTML 翻訳プログラム Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds,
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
を日本語化したもの( 2002-2-1 (1.71) JA patch-1.9 版)
Copyright © 1998, 1999, Kenshi Muto, Debian Project.
Copyright © 2000, Jun Nishii, Project Vine.
Copyright © 2001, 2002, Shige TAKENO, Niigata Inst.Tech.
Copyright © 2002, KOBAYASHI R. Taizo, Project Vine.
を用いて生成されました。
コマンド行は以下の通りでした。:
latex2html -nomath_parsing -local_icons -show_section_numbers -split 0 note1-e.tex.
翻訳は Jun Makino によって 平成25年7月17日 に実行されました。