そもそもカオスとは何でなぜそういうものを考えるかというところから話を始め る必要がある。
というわけで、定義から始めたいところだが、一応ここでは
ものをカオスということにする。
そういうものはいくらでもあるわけだが、まず、カオスで「ない」ものの例か ら考えていこう。
球対称ポテンシャルの中での粒子の運動はカオスではな い。これは、軌道が単純な動径方向の振動と角度方向の振動に分離できるから である。
これが、軸対称ポテンシャルになるともういきなり話がわからなくなる。
軸対称なので円筒座標 ![]() を考えると、ポテンシャル
を考えると、ポテンシャル ![]() の中
で
の中
で ![]() 軸回りの角運動量
軸回りの角運動量 ![]() を持つ粒子の運動は、有効ポテンシャル
を持つ粒子の運動は、有効ポテンシャル
| (1) |
Henon と Heiles (1964 AJ 69, 73) は、 ![]() として以下のようなものを考
えてみた。
として以下のようなものを考
えてみた。
| (2) |
何故この形を考えたかというのは、論文には以下のように書いてある
because: (1) it is analytically simple; this makes the computation of the trajectory easy; (2) at the same time, it is sufficiently complicated to give trajectories which are far from trivial, as will be seen below.
つまり、物理的あるいは天文学的になにかの意味があるというよりは、このポ テンシャルの中での軌道の振る舞いが妙であるということで選ばれたかなり人 工的な例ではある。
もちろん、最初の項は調和振動であり明確な意味がある。非線型の第2項の意 味はポテンシャルの等高線を書いて見ると分かる。
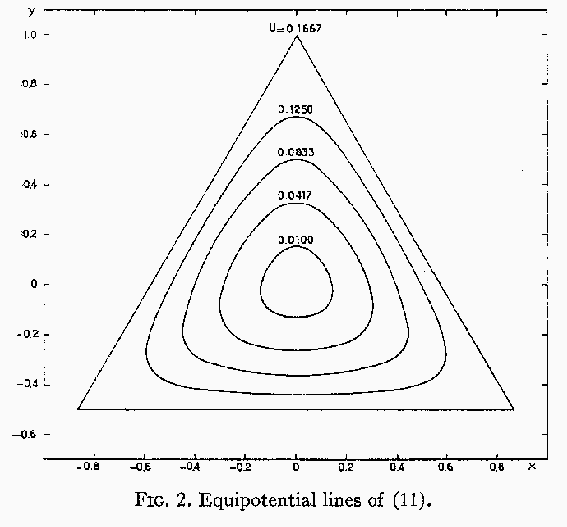
このように、非線型項によりポテンシャルが三角形になっている。特に
![]() の等高線に注意すると、これは直線になっている。このことから、こ
の三角形の頂点はポテンシャルの鞍点であり、力が 0 になることが分かる。
の等高線に注意すると、これは直線になっている。このことから、こ
の三角形の頂点はポテンシャルの鞍点であり、力が 0 になることが分かる。
鞍点であるので、ポテンシャルが下がるのは三角形の内側を向いた方向とその 反対側の方向だけであり、それに直交する方向ではポテンシャルは増えている。 また、頂点以外では力は 0 でない。
軌道は例えばこんなふうである。これはエネルギー(ハミルトニアン)
| (3) |
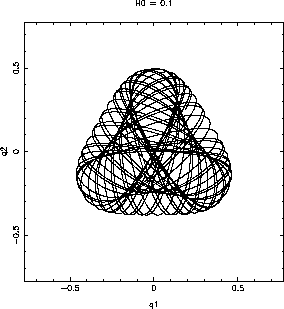
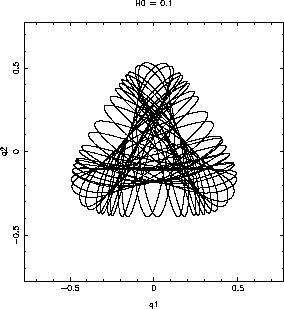
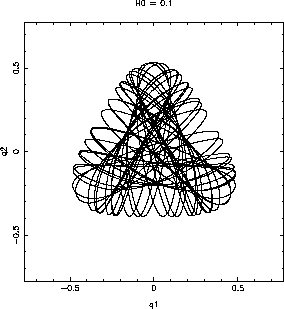
これだけを見ていると別にどうということはないが、ここでいわゆるポアンカ
レ断面というものを書いて見ると非常に面白いことになっていると分かる。ポ
アンカレ断面とは、 この場合のような自由度が2のハミルトン力学系で、一方
の変数、例えば ![]() が 0 になる時に
が 0 になる時に ![]() ,
, ![]() の値を書いたものである。
の値を書いたものである。
まず、 ![]() の場合を示す。
の場合を示す。
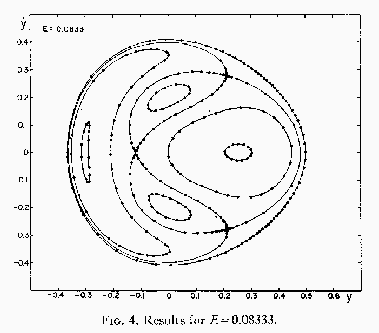
ここで、つながって線になっているのは基本的には一つの軌道であり、分かれ
た曲線は別の初期条件からの軌道に対応している。エネルギー保存を考えると、
![]() で
で ![]() なので、
なので、 ![]() ) はある閉領域の中にくる。保存
量がエネルギーだけであれば、任意の初期条件から出発した軌道はこの領域の
全ての点をいつかは通ると考えられるが、 このようにそうならないというこ
とは、なんだかわからない保存量のようなものがあるということを示している。
元々の軸対称ポテンシャルに戻ると軸回り角運動量は保存しているが、これは
有効ポテンシャルにして回転方向の速度を消去するのに使っているので、2次
元問題になった後では無関係である。
) はある閉領域の中にくる。保存
量がエネルギーだけであれば、任意の初期条件から出発した軌道はこの領域の
全ての点をいつかは通ると考えられるが、 このようにそうならないというこ
とは、なんだかわからない保存量のようなものがあるということを示している。
元々の軸対称ポテンシャルに戻ると軸回り角運動量は保存しているが、これは
有効ポテンシャルにして回転方向の速度を消去するのに使っているので、2次
元問題になった後では無関係である。
軸対称ポテンシャル内での運動にエネルギーと角運動量以外の保存量があるか どうかという問題は、「第3積分問題」と呼ばれる恒星系力学上の現在でも完 全には解決されているとはいいがたい問題の一つである。 とりあえずこの場 合には、第3積分が存在しているように見える。
但し、妙なのは、ポアンカレ断面上の軌跡が交点をもつように見えることであ る。実際には、この「交点」のところを精密に調べると、奇妙なことがわかる。 交点近くの十分に狭い領域では運動の積分が無くなって、ある領域内を軌道が 埋めているのである。
この領域はエネルギーを大きくするとどんどん大きくなる。次は ![]() の場合である。
の場合である。
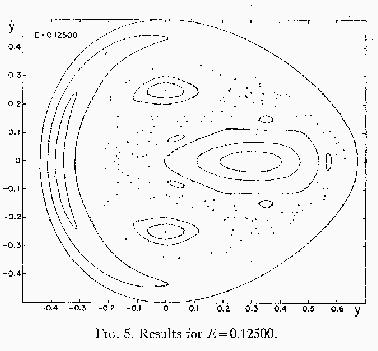
保存量を持つ、規則的な運動をする領域よりも、規則的ではない運動をする領 域のほうが広くなってしまっていることが分かる。少なくとも恒星系力学では、 このような場合に 規則的な軌道を regular orbit, そうでないものを irregular orbit または chaotic orbit という。
さらにエネルギーの上限に近い
![]() をとったものが下である。
をとったものが下である。
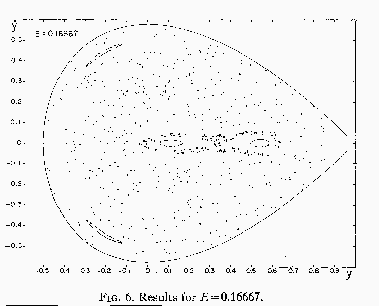
キャプションには ![]() よりも大きいようなことが書いてあるが、気の迷い
であろう。それはともかく、この場合にはほとんどの領域が規則的でない、つ
まり、第3積分をもたないような軌道になっていることが分かる。
よりも大きいようなことが書いてあるが、気の迷い
であろう。それはともかく、この場合にはほとんどの領域が規則的でない、つ
まり、第3積分をもたないような軌道になっていることが分かる。
これはカオス的な運動の典型的な例である。
ここではカオスかどうかを、エネルギー以外の積分がある(ように見える)かど うかで判断したが、実質的に同じことになるもうひとつの定義がある。それは、 「十分に近い初期条件から出発した2つの軌道がどのように離れていくか」で ある。より厳密にはこれはリヤプノフ指数が正かどうかということになる。定 義の詳細はここでは省くが、大雑把にはリヤプノフ指数が正なら十分近い2つ の軌道が指数関数的に離れていく。このことは上の Hnon-Heiles 系でも観 察され、周期的に見える領域では軌道は時間の1次で離れていくが、カオス的 な領域では指数関数的に離れる。