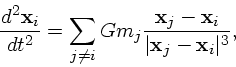 |
(1) |
今日は、一回目ということでとりあえず無衝突ボルツマン方程式を導いてその 振舞いについて少し考える。
恒星系力学の基礎方程式は何かというと、原理的には恒星系は自己重力多体系 と考えていいわけで、各粒子(恒星)の運動方程式
が基礎方程式ということになる。
数値計算にはもちろんこれを使うわけだが、理論的な扱いには不便である。
というわけで、しばらくは(1粒子)分布関数
![]() で話をする。
ここでは、粒子数が「無限に大きい」と思って、6次元の位相空間
で話をする。
ここでは、粒子数が「無限に大きい」と思って、6次元の位相空間
![]() の中の粒子の密度分布の時間進化を考える。
この時の基礎方程式が(無衝突)ボルツマン方程式である。
の中の粒子の密度分布の時間進化を考える。
この時の基礎方程式が(無衝突)ボルツマン方程式である。
以下、方程式を導く。位相空間での座標を
![]() と書くこと
にする。また、重力ポテンシャルを
と書くこと
にする。また、重力ポテンシャルを
![]() とおくと、位相空間
の中での粒子の流れは
とおくと、位相空間
の中での粒子の流れは
| (2) |
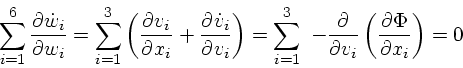 |
(4) |
| (6) |
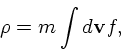 |
(7) |
なお、以下の議論では(当分) ![]() のことは忘れて、その代わり
のことは忘れて、その代わり ![]() が個数
密度ではなくて質量分布であるということにしておく。
が個数
密度ではなくて質量分布であるということにしておく。
直観的な意味は
で、これが ![]() : 非圧縮での連続の式
: 非圧縮での連続の式