ここであげるのはあくまでも例であるが、さまざまな理由からその性質がよく 調べられているものである。
先週やったプラマーモデルはその存在が100年くらい前から知られているが、こちらは論文が発表
されたのが 1990 年(というわけで、 Binney & Tremaine の初版のときにはまだ知
られていなかった)という、割合新しいモデルである(Hernquist, L.,
1990, ApJ 356, 359)。これは、ポテンシャルを
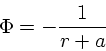 |
(5) |
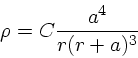 |
(6) |
| (7) |
Hernquist Model には、「![]() 則をかなり良く再現する」という著しい特
徴がある。
則をかなり良く再現する」という著しい特
徴がある。
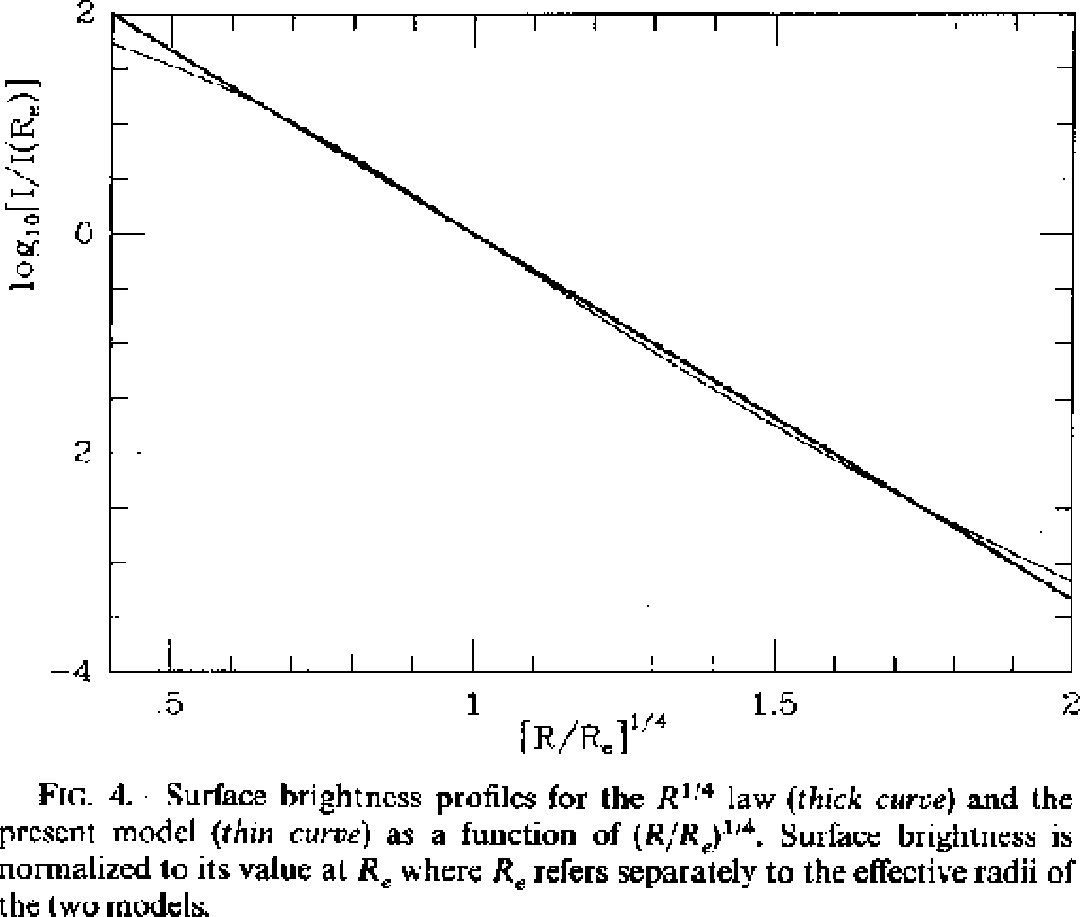
![]() 則については後でその物理的解釈も含めて詳しく議論することにし
たいが、要するに、観測される楕円銀河の表面輝度の対数(要するに等級です
ね)が、半径の
則については後でその物理的解釈も含めて詳しく議論することにし
たいが、要するに、観測される楕円銀河の表面輝度の対数(要するに等級です
ね)が、半径の![]() 乗に対して直線にのって見えるというものである。この
性質と、一応解析関数で分布関数が書けるということのために、楕円銀河やダー
クハローのモデルとして広く使われるようになってきている。
乗に対して直線にのって見えるというものである。この
性質と、一応解析関数で分布関数が書けるということのために、楕円銀河やダー
クハローのモデルとして広く使われるようになってきている。
ただし、このモデルにはいくつか妙な性質もあり、それについてもまた後で触 れることになるはずである。
無衝突ボルツマン方程式の定常解は熱平衡とは限らない。また、無衝突ボルツマン方程式に従った進化ではそもそもエ
ントロピーが発生しない。 (![]() の値がラグランジュ的には変化しないから)
従って、系が熱平衡に向かって進化するとも限らない。
が、それでも、熱平衡状態に
ついて良く理解しておくことは結構大事である。
熱平衡状態では(古典統計なので)分布関数はマックスウェル-ボルツマン分
布、すなわち
の値がラグランジュ的には変化しないから)
従って、系が熱平衡に向かって進化するとも限らない。
が、それでも、熱平衡状態に
ついて良く理解しておくことは結構大事である。
熱平衡状態では(古典統計なので)分布関数はマックスウェル-ボルツマン分
布、すなわち
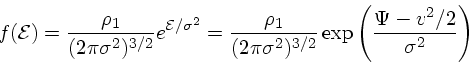 |
(8) |
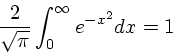 |
(9) |
| (10) |
 |
(11) |
 |
(12) |
 |
(13) |
特に、渦巻銀河については、「回転速度が中心からの距離に(あまり)依存し
ない」(いわゆる flat rotation curve)という性質が知られていて、これを
説明するためには上のような
![]() のダークハローが必要である
ということになっている。
のダークハローが必要である
ということになっている。
特別ではない解は、中心密度を有限にして中心から外側に向かって解いていけ
ばいい。この時でも、
![]() の極限では singular
isothermal に近付く。
の極限では singular
isothermal に近付く。
等温モデルは、エントロピー極大であり、分布関数がボルツマン分布になって
いるという特別な性質がある。このため、等温ガス球と実は同じ構造をとる。
以下、ガス球について方程式を導いておく。
静水圧平衡の式は
| (14) |
| (15) |
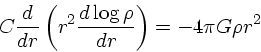 |
(16) |
なお、ポリトロープでも、ポリトロピックな状態方程式を持つガス球の密度分 布と stellar system のそれとは一致する。が、等温モデルの場合とは実は本 質的な違いがある。等温モデルの場合は、分布関数そのものが一致する(ボル ツマン分布であり、局所的にも大局的にもエントロピー最大)が、一般のポリ トロープではそんなことはない(そもそもガス球ではジーンズの定理が成り立 たないし、局所的にはボルツマン分布であるから)。
等温モデルは、すでに述べたように熱平衡(エントロピーの変分が 0 )とい う重要な意味を持つ定常解ではあるが、なにしろ質量が無限大であり現実に存 在しないのでちょっと困るところがある。なにか適当な仮定を置くことで、 「おおむね等温モデルであり、なおかつ有限の大きさをもつ」というものを考 えることはできないだろうか?
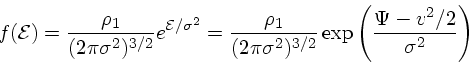 |
(17) |
上の分布関数で、質量が発散する理由は何かを思い出してみよう。その本質的
な理由は、分布関数がエネルギー無限大 (
![]() )ま
で0にならないことにある。
)ま
で0にならないことにある。
有限の質量のものが自己重力でまとまっているためには、すべての粒子のエネ ルギーが負でないといけないので、これでは自己重力系が表現出来ないのはあ る意味では当然のことといえる。
それならば、ある有限のエネルギー以上のものはないことにしてしまえばいい。 そのやり方にはいろいろあり得るが、とりあえず Lowered Maxwellian と呼ば れる以下のようなものを考える
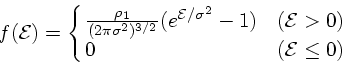 |
(18) |
これは![]() で
で ![]() となるように、 1 を引いたというだけである。
これしか方法がないというわけではないが、これは扱いやすいこともあってもっ
ともよく使われている。
となるように、 1 を引いたというだけである。
これしか方法がないというわけではないが、これは扱いやすいこともあってもっ
ともよく使われている。
これはいかにも人工的な感じがすると思うが、等温モデルから有限質量でなお かつ有限半径のモデルにするもっとも簡単な方法なので、まあ、そういうもの と思って欲しい。
例によって、まず速度空間で積分すれば
![$\displaystyle {4\pi \rho_1 \over (2\pi \sigma^2)^{3/2}}\int_0^{\sqrt{2\Psi}}
\left[\exp\left({\Psi - v^2/2 \over \sigma^2}\right) -1
\right]v^2dv$](img44.png) |
|||
![$\displaystyle \rho_1 \left[e^{\Psi/\sigma^2} {\rm erf}\left({\sqrt{\Psi \over
\...
...\sqrt{4\Psi \over \pi \sigma^2}\left(1 + {2\Psi
\over 3 \sigma^2}\right)\right]$](img45.png) |
(19) |
ここで ![]() は誤差関数で、積分が有限区間であるために出てくる。最後の項
は1引いている分の寄与である。ちなみに
は誤差関数で、積分が有限区間であるために出てくる。最後の項
は1引いている分の寄与である。ちなみに
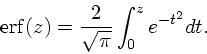 |
(20) |
これでポテンシャルの関数として密度が求まったので、あとはポアソン方程式 に入れて数値的に解くだけである。ただし、 King model の場合境界条件につ いてすこしきちんと考える必要がある。
半径方向の分布は、中心から無限遠まで与えられるわけであるが、実は外側の 境界をどうとるべきかはちょっと自明ではないので、とりあえず中心から初期 値問題として解くことを考える。
初期条件としては、まず ![]() とする、すなわち、中心密度が有限
の解を考える。
とする、すなわち、中心密度が有限
の解を考える。 ![]() は任意に選べるので、これの値によっていろいろな
解がでてくる。
は任意に選べるので、これの値によっていろいろな
解がでてくる。
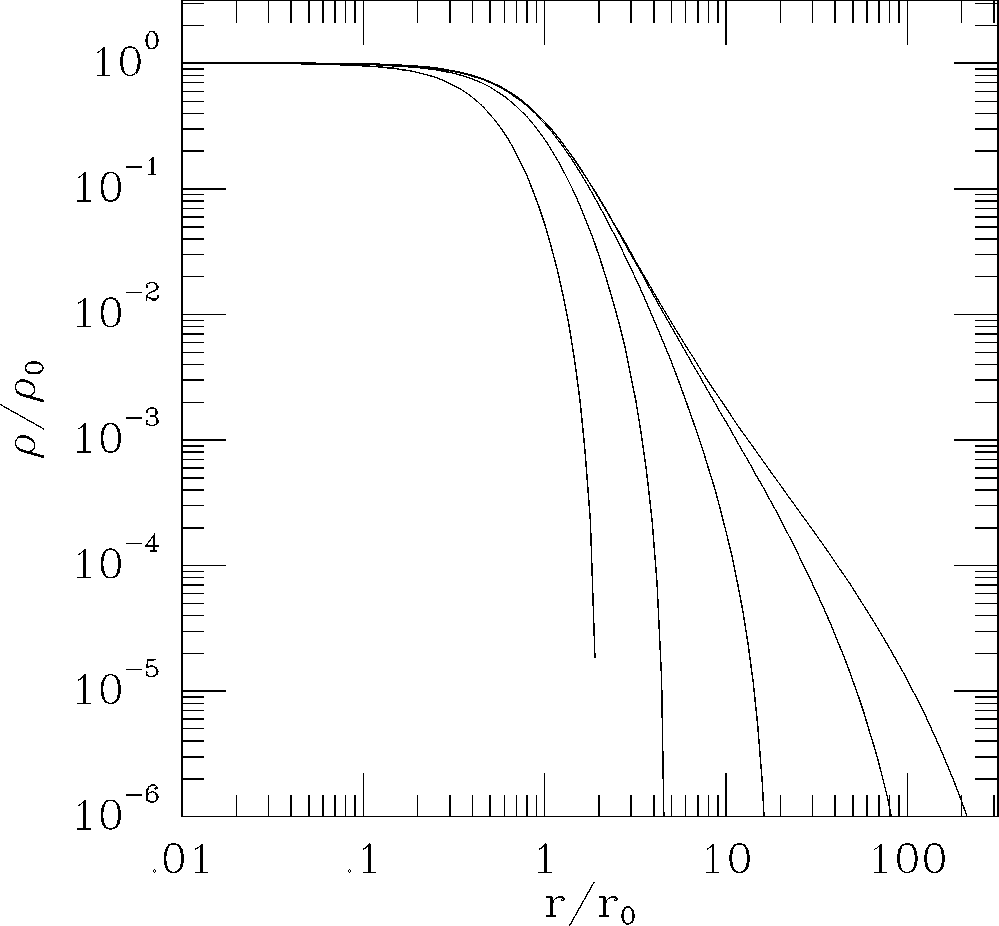
これは実際に数値的に解いてみたものの例である。速く落ちるものから、
![]() が 1, 3, 6, 9, 12 と変えてみてある。
が 1, 3, 6, 9, 12 と変えてみてある。
なお、横軸のスケールの ![]() は、
は、
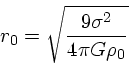 |
(21) |
グラフからわかるように、有限の半径 ![]() で
で ![]() は 0 になる。これは、
解いていったときに
は 0 になる。これは、
解いていったときに ![]() が 0 になってしまうためである。この半径のこ
とを King model の tidal radius 潮汐半径という。このモデルのばあい、
が 0 になってしまうためである。この半径のこ
とを King model の tidal radius 潮汐半径という。このモデルのばあい、
![]() と本当のポテンシャル
と本当のポテンシャル ![]() の間に以下のような簡単な関係が成り立
つことに注意。
の間に以下のような簡単な関係が成り立
つことに注意。
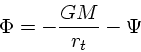 |
(22) |
King Model は、球状星団のプロファイルのモデルとして非常によく使われて
いる。なお、
![]() のことを concentration parameter といっ
て、観測データにキングモデルを合わせた論文では普通これがパラメータにな
る。理論計算では
のことを concentration parameter といっ
て、観測データにキングモデルを合わせた論文では普通これがパラメータにな
る。理論計算では ![]() が使われるので、ちょっとややこしいことが多い。
が使われるので、ちょっとややこしいことが多い。
さて、今まで、単に無衝突ボルツマン方程式の球対称定常解というものの例を いろいろ見てきたわけだが、ちょっと飽きてきたので目先を変えてみよう。具 体的には、「球対称の恒星系のなかでのガスの分布」というものを考えてみる ことにする。というのは、現在でも観測データの解釈に使われている簡単なモ デルは、現在までにやった範囲で十分カバーできるものになっているからであ る。
多くの銀河団には高温ガスが存在しており、X線で観測可能である。
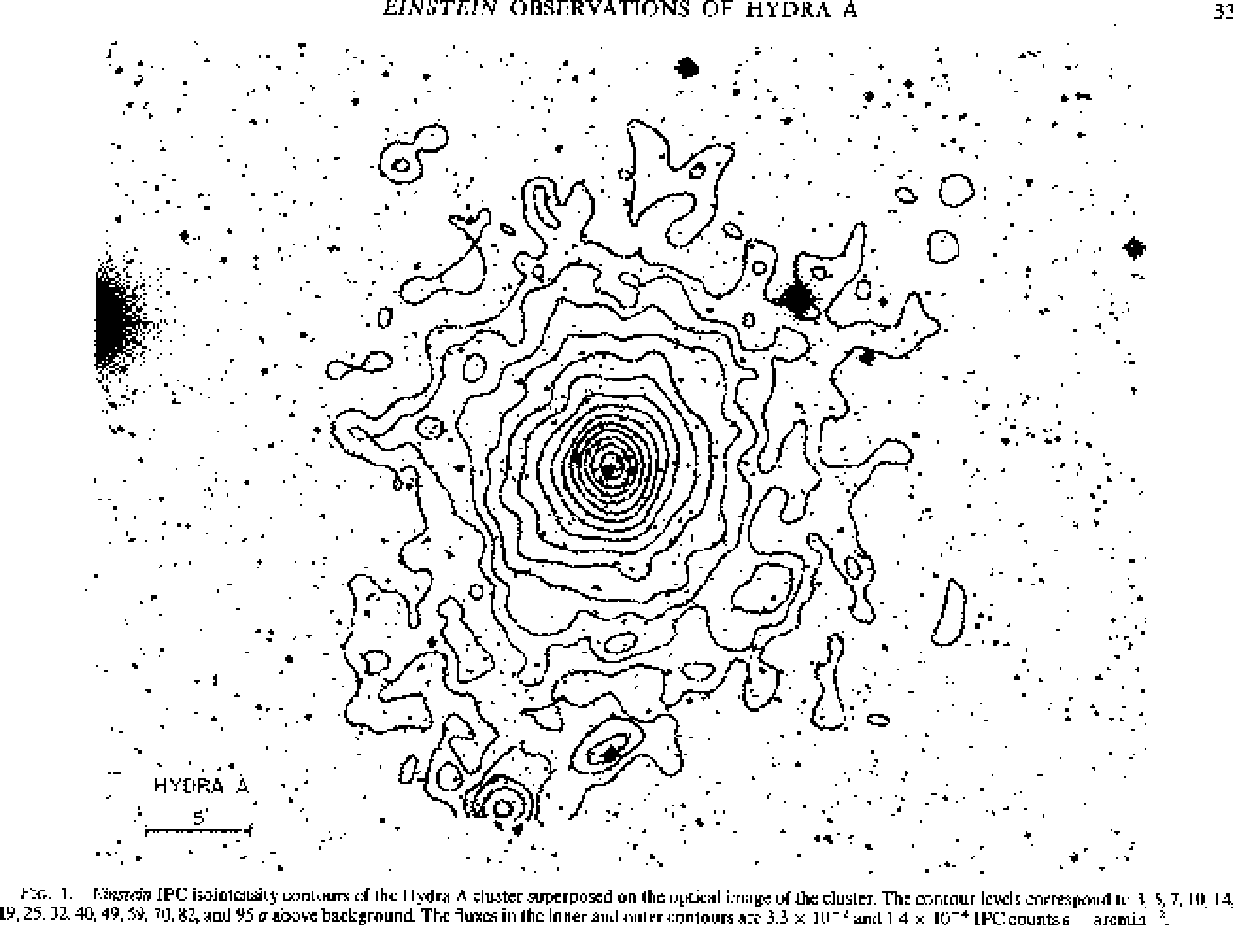
上は Einstein IPC による Hydra A 銀河団に(David et al. ApJ 1990, 356, 32) の像である。あと、 Chandra やすざくのとか見たことがある人も多いと思 うが、まあだいたいこんな感じにきれいに丸いのが普通である。 X 線ガスの 振舞いについての詳しい話は Sarazin の教科書かなにかを見てもらうとして、 とりあえず重要なのは、
まず、話を簡単にするために、
さて、これぐらいたくさん仮定すると、美しい理論を構築できることになる。
まず、ガスの速度分散と恒星系の速度分散が等しい場合というのを考えてみる。
ガスの密度![]() が従う方程式は、星の密度を
が従う方程式は、星の密度を ![]() として
として
| (24) |
では、温度(速度分散)が違う場合はどうなるかが問題である。ガスの温度
![]() と、恒星系に対応する「温度」
と、恒星系に対応する「温度」 ![]() の比を
の比を
![]() と置
くと、
ガスの密度が従う方程式は、
と置
くと、
ガスの密度が従う方程式は、
![\begin{displaymath}
% latex2html id marker 173{d \over dr} \left(r^2 {d \log ...
...g} \over dr}\right) =\beta[式
(\ref{eq:isotemperature})の右辺]
\end{displaymath}](img67.png) |
(25) |
と、ここまではちゃんと正しい話をしてきたが、実際に観測結果の解釈に使う
時にはさらに大胆な近似がなされる。以下、 Sarazin の X-ray emissions
from clusters of galaxies 5.5節に従っていわゆる![]() モデルについて説
明し、その問題点について検討する。
モデルについて説
明し、その問題点について検討する。
式(26)はもちろん正しいし、有用なものではあるが、あま
り使い回しがよくない。というのは、![]() のほうがそもそも数値的にしか
求まっていないからである。というわけで、
のほうがそもそも数値的にしか
求まっていないからである。というわけで、![]() をなにか解析関数で置き
換えることを考える。さて、以下の質量分布
をなにか解析関数で置き
換えることを考える。さて、以下の質量分布
| (27) |
| (28) |
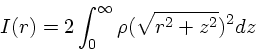 |
(29) |
| (30) |
左はうまくいく例である (Jones and Forman 1984)。右は先ほど見せた Hydra A
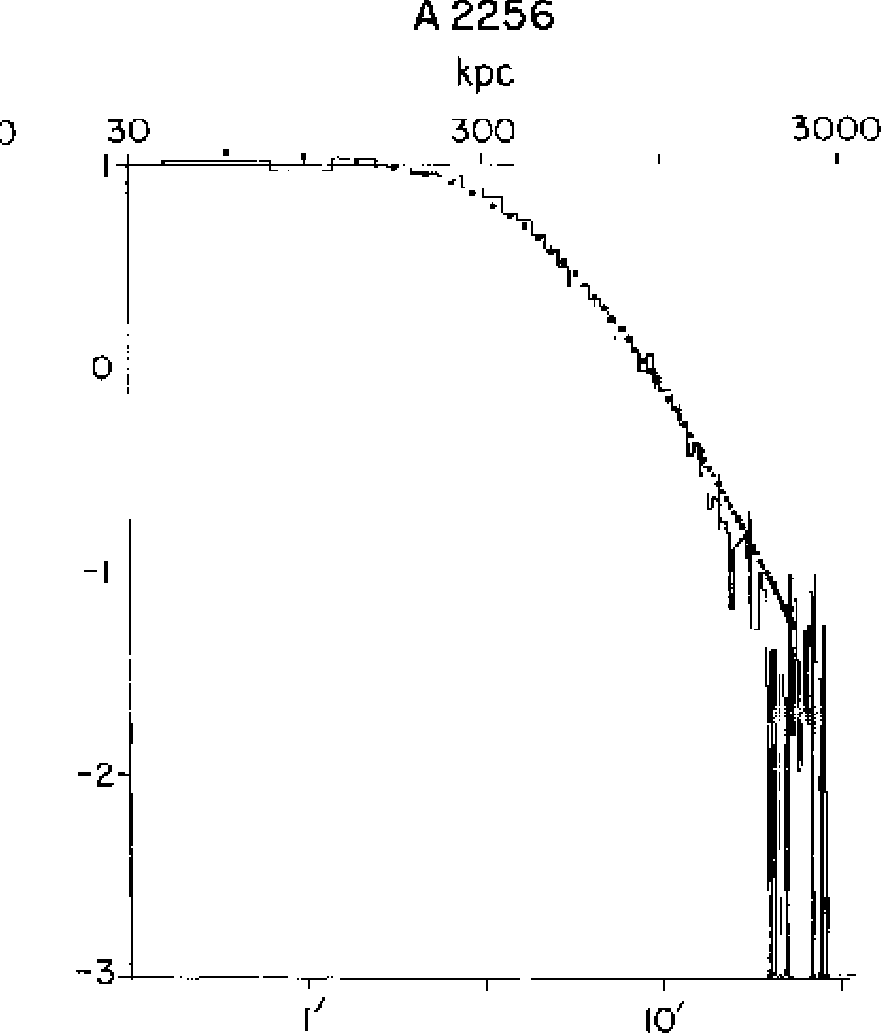 =6cm
=6cm
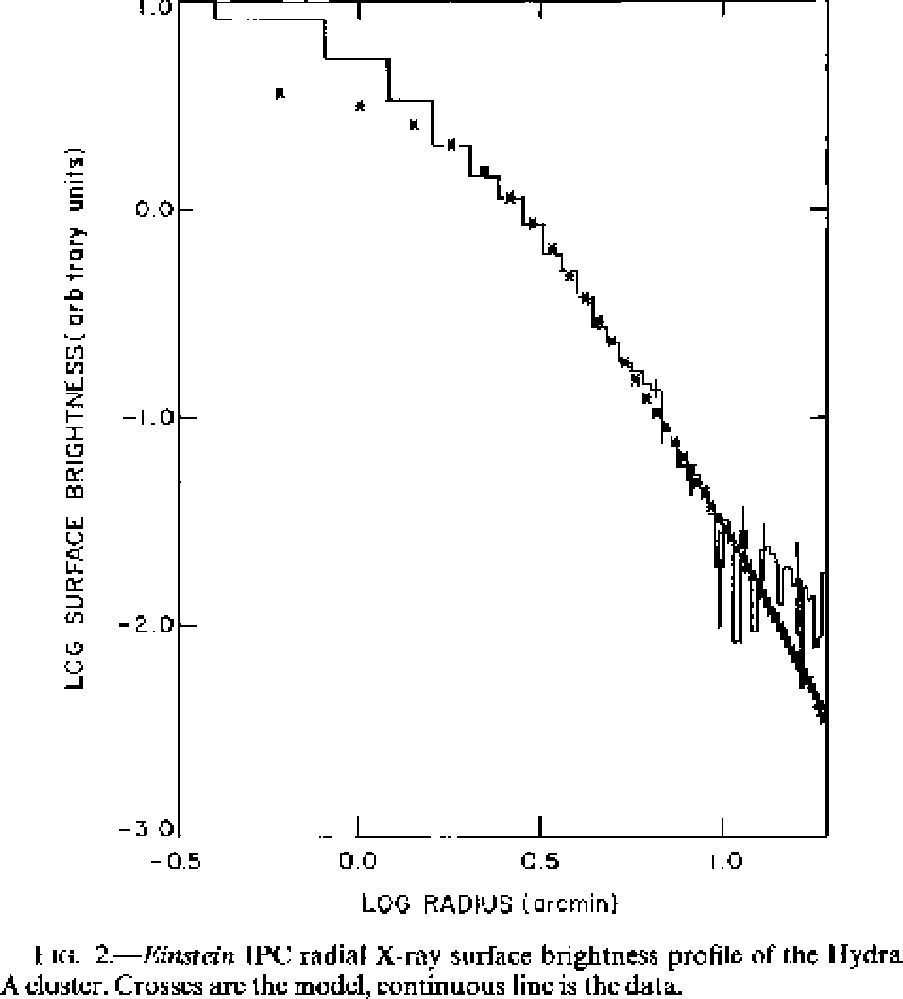
これらはそれなりに典型的なものだが、もうちょっと最近の論文(Ikebe et al. 1997, ApJ 481, 660)をあげておくと
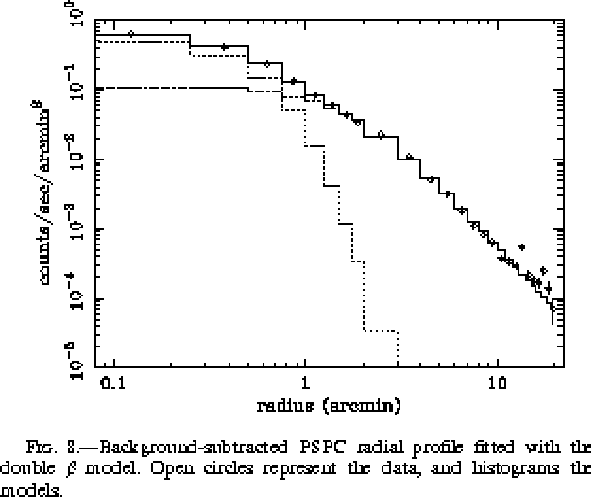
いくつかの観測結果をこのように ![]() モデルでフィットした結果から、以
下のような問題があるということになっている。
モデルでフィットした結果から、以
下のような問題があるということになっている。
これが問題であるかどうかについては、例えば以下のようなことも考慮する必 要があろう。
と、いうわけで、レポート用課題(1)