| (1) |
ここまで、自己重力多体系の平衡形状を(ごく簡単な場合だけ)扱ってきたが、 今回からは平衡形状ではなく時間発 展について考えることにしたい。
時間発展といっても、もとの方程式が強い非線形性を(加速度の項に)持つの で、一般的な場合を解析的に扱うことはほとんど出来ない。そこで、ま ず、平衡状態から無限小だけずれている場合に対して線形化した発展を考える ということにする。さらに、話を簡単にするために、「無限一様」な平衡状態 とし、まずCBE ではなく流体の話を考える。
流体は、連続の式
| (1) |
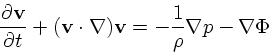 |
(2) |
| (3) |
今、
![]() をそれぞれ
をそれぞれ
![]() という格好にして、添字 0 がつくものはもとの方程式の平衡解であ
り、
という格好にして、添字 0 がつくものはもとの方程式の平衡解であ
り、 ![]() がつくものは小さい(二次以上の項を無視していい)として方程式を
書き直すと
がつくものは小さい(二次以上の項を無視していい)として方程式を
書き直すと
| (4) |
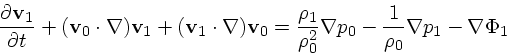 |
(5) |
| (6) |
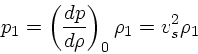 |
(7) |
既に述べたように、無限一様でいたるところ密度、圧力が等しいというのが平
衡で、速度も0だったとすると、上の2本は
| (8) |
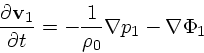 |
(9) |
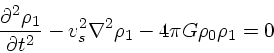 |
(10) |
最初の2項をみれば普通の波動方程式で、最後の項がポアソン方程式を通して でてくる重力の項である。したがって、波長が短い極限では普通の波動方程式 に近付く。これに対し、波長が長い極限では空間2階微分の項が効かなくなる ので、線形の常微分方程式になってしまう。
実際に分散関係を求めるために、解を
| (12) |
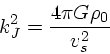 |
(13) |
なお、一応念のために書いておくと、式(11)の形の解だけを 考えるのは任意の初期条件からの解が(連続性とかを仮定すれば)この形の解 の線形結合で表現できるからである。解の線形結合が解であるのは方程式が線 形だからであり、任意の解が表現できるのは要するにフーリエ変換が完全系を なすからである。
話を戻すと、定性的に見たときにわかったように、波長が短ければ普通の音波
として振舞うが、波長が ![]() より長いと時間の指数関数で進化すること
になる。つまり、密度が上がり始めたらどんどんあがる(下がり始めたらどん
どんさがる)ということになる。
より長いと時間の指数関数で進化すること
になる。つまり、密度が上がり始めたらどんどんあがる(下がり始めたらどん
どんさがる)ということになる。
ここで注意して欲しいのは、十分に波長が長いと必ず不安定になるということ である。これはつまり、重力があると無限に一様な状態というのは温度無限大 でない限り必ず不安定であるということである。
さて、 ![]() というのは直観的にはどういうものかというのを考えてみる。
というのは直観的にはどういうものかというのを考えてみる。
![]() は波数なので、その逆数に
は波数なので、その逆数に ![]() を掛けると波長になる。これをジー
ンズ波長
を掛けると波長になる。これをジー
ンズ波長 ![]() といって、式にすると
といって、式にすると
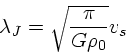 |
(14) |
今、半径がジーンズ波長くらいの球を考えてみる。これの単位質量当りの運動
エネルギー(熱エネルギー)は、もちろん ![]() の程度である。これに対し
て重力エネルギーは
の程度である。これに対し
て重力エネルギーは
![]() の程度、ここで
の程度、ここで ![]() はジーンズ質
量で半径
はジーンズ質
量で半径 ![]() の球の質量である。
の球の質量である。 ![]() に上の式を入れて計算すると、結局
重力エネルギーが定数を別にして
に上の式を入れて計算すると、結局
重力エネルギーが定数を別にして ![]() の程度になることがわかる。
の程度になることがわかる。
つまり、熱エネルギーより重力エネルギーが大きくなるような長さの摂動は成 長するということになる。