

次へ: 2 2体緩和のタイムスケール
上へ: 天文学特別講義IV
戻る: 天文学特別講義IV
Subsections
というわけで、いよいよバックグラウンドが動いている場合ということになる。
この時でも、相対速度の変化自体は前節に述べたもので正しいが、相対速度に
フィールド粒子の速度成分が入ってくることになる。
以下、二種類の単位ベクトル系をとって、その上で考える。一つは
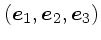 であり、元の空間に固定されている。もう一つは
であり、元の空間に固定されている。もう一つは
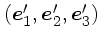 であり、最初の成分を相対速度
であり、最初の成分を相対速度
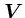 に平行にとる。従って、
後者は相手の粒子によって違うわけである。この2つを考えることで、相対速
度の変化をもとの静止系でのテスト粒子の変化に焼き直す。
に平行にとる。従って、
後者は相手の粒子によって違うわけである。この2つを考えることで、相対速
度の変化をもとの静止系でのテスト粒子の変化に焼き直す。
まず、1次の項は相対速度に平行な成分だけであった。このことから、ある方
向の速度変化は
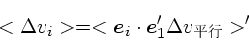 |
(1) |
ということになる。もうすこし精密に書くと、右辺はインパクトパラメータと
相手の速度の積分なので、以下のように書けることになる。
ここで、
 はフィールド粒子の速度、
はフィールド粒子の速度、 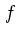 は速度分布
関数である。
は速度分布
関数である。 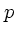 についての積分を先にやったことに注意して欲しい。この積
分は
についての積分を先にやったことに注意して欲しい。この積
分は 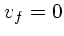 であった時の結果をそのまま使っている。
であった時の結果をそのまま使っている。
さて、2次の項についてであるが、前節で見たように
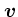 に垂直な成分、す
なわち
に垂直な成分、す
なわち
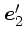 と
と
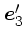 の成分を考えればいい。従って、一つの方向から
くるフィールド粒子との散乱を考えた時には
の成分を考えればいい。従って、一つの方向から
くるフィールド粒子との散乱を考えた時には
これもまた分布関数を掛けて積分すると、結局
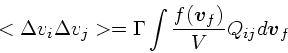 |
(5) |
ということになる。これで一応必要な2次までの係数はすべて書けたわけだが、
あまり計算するのに使い易い形ではない。というのは、
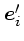 とか
とか 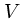 と
かいったものがまだややこしい形ではいったままであるからである。しかし、
もうちょっと簡単な形に書き直せることが知られている。まず、1次の項だが、
と
かいったものがまだややこしい形ではいったままであるからである。しかし、
もうちょっと簡単な形に書き直せることが知られている。まず、1次の項だが、
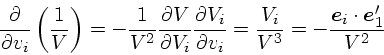 |
(6) |
という都合のよい関係がある。変形はとくにややこしいところはないと思う。
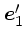 をそもそも
をそもそも
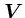 に平行にとったから上のように出来るわけである。
このため、
に平行にとったから上のように出来るわけである。
このため、
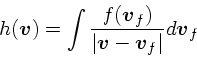 |
(7) |
なる関数
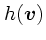 を導入して、
を導入して、
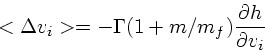 |
(8) |
ということになる。
2次の項についても同様な整理が可能である。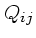 は
は
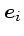 ,
,
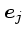 の
の
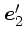 と
と
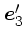 によって張られる平面への写像の内積なので、
によって張られる平面への写像の内積なので、
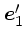 と
の内積の分をつけてやれば元の単位ベクトル同士の内積になる。つまり、
と
の内積の分をつけてやれば元の単位ベクトル同士の内積になる。つまり、
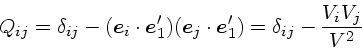 |
(9) |
したがって、
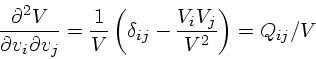 |
(10) |
というわけで、
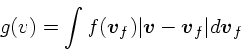 |
(11) |
とおけば、
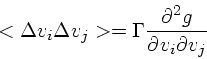 |
(12) |
前節では、バックグラウンドの速度分布が任意のものについて、実際に計算可
能な式を導いた。ここでは、速度分布が等方的な場合につ
いて式を単純化してみる。
速度分布が等方的な場合、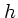 や
や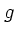 の積分を、
の積分を、
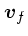 の絶対値方向と角度方
向に分けることができる。角度方向の積分については、
の絶対値方向と角度方
向に分けることができる。角度方向の積分については、
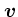 と
と
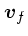 の
なす角度を
の
なす角度を 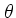 とし、
とし、
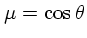 とすれば、球面上での積分
が、まず
とすれば、球面上での積分
が、まず については
については
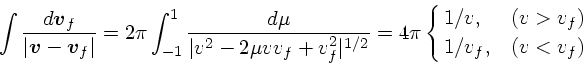 |
(13) |
となる。これは、球面上に分布する電荷の作るポテンシャルと同じ式である。
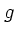 についても同様に計算できて
についても同様に計算できて
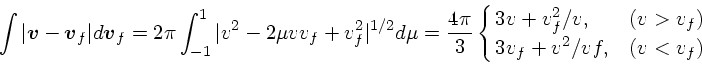 |
(14) |
となる。これから、
というものを考えると、
これらから、最終的な結果、すなわち、バックグラウンドが動いている時の、
速度に平行な速度変化と垂直なそれを書き下せることになる。それらは、結局、
これらから、粒子のエネルギーの変化 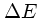 を出すことができる。
を出すことができる。
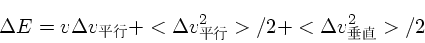 |
(20) |
と書けるので、1次の項は
![\begin{displaymath}
<\Delta E> = 4 \pi \Gamma v\left[E_1(v) -{m \over m_f}F_2(v)\right]
\end{displaymath}](img60.png) |
(21) |
となる。2次の項については、
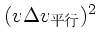 以外の項は小さいので
無視すると
以外の項は小さいので
無視すると
![\begin{displaymath}
<\Delta E^2> = {8 \pi \Gamma v^3 \over 3} \left[F_4(v) +E_1(v)\right]
\end{displaymath}](img62.png) |
(22) |
となる。
さて、速度分布を熱平衡、すなわち
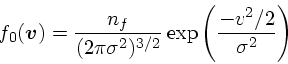 |
(23) |
とすると、上の係数等を具体的に計算できることになって、その形は
ここで 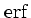 は誤差関数であり、
は誤差関数であり、
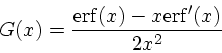 |
(28) |
また
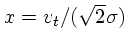 である。
である。
山ほど式はでてきたものの、全然なんだかわからないという気分になった人も
まあいるのではないかと思うので、以下、上の式の意味についてちょっと考え
てみよう。
まず、速度の1次の項を見てみる。これは、速度分布には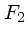 だけ
を通して依存しているということに注目して欲しい。例えば、マックスウェル
分布のようなものを考えた時、
だけ
を通して依存しているということに注目して欲しい。例えば、マックスウェル
分布のようなものを考えた時、 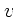 が大きい極限では
が大きい極限では
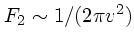 となるので、回りが止まっているときと同じく速度変化は速度の2乗に
反比例する。これに対して、
となるので、回りが止まっているときと同じく速度変化は速度の2乗に
反比例する。これに対して、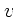 が小さい極限では、
が小さい極限では、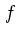 を一定と見なすことが
出来るので
を一定と見なすことが
出来るので 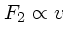 となる。
となる。
これは、タイムスケールを考えてみると、速度が大きい極限では減速のタイム
スケールが 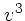 であるのに対し、逆の極限では 一定になるということであ
る。すなわち、非常に速度が大きい粒子が出来てしまうとこれはなかなか減速
しない。もちろん、自己重力系の場合には、そのようなものは系のなかに留ま
るのが困難だということもあるが。
であるのに対し、逆の極限では 一定になるということであ
る。すなわち、非常に速度が大きい粒子が出来てしまうとこれはなかなか減速
しない。もちろん、自己重力系の場合には、そのようなものは系のなかに留ま
るのが困難だということもあるが。
これに対し、速度が小さいほうではタイムスケールがある一定値、つまりは
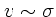 で決まる値あたりになるということである。
で決まる値あたりになるということである。
この1次の項は、前に述べたように dynamical friction を表している。これ
が問題になる場面は、例えば恒星系が質量の違う2つの成分から出来ているよ
うな場合である。力学平衡で、分布関数に質量依存がないようなものを考える
と、これは熱平衡から遠くはなれている。従って、上の式で決まるタイムスケー
ルで重いものがエネルギーを失い、軽いものがエネルギーを得る。
なお、、自己重力系ではこのエネルギー交換の結果熱平衡に向かうとは限らな
いということに注意する必要がある。つまり、重いものがエネルギーを失い、
軽いものがエネルギーを得るということは、それぞれの分布関数が変わり、空
間分布も変わるということである。具体的には、重いものは中心に落ちるし、
軽いものは外側に押し出される。
さて、次に、2次の項を見てみる。速度に平行な成分も垂直な成分も、 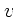 が
大きい極限では0にいく。特に、 垂直な成分は
が
大きい極限では0にいく。特に、 垂直な成分は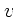 に反比例する。これに対し、
速度が
に反比例する。これに対し、
速度が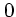 の極限では、どちらも一定値に収束する。これは停止している極限
でも、回りの粒子によって揺さぶられるということを表しているわけである。
の極限では、どちらも一定値に収束する。これは停止している極限
でも、回りの粒子によって揺さぶられるということを表しているわけである。


次へ: 2 2体緩和のタイムスケール
上へ: 天文学特別講義IV
戻る: 天文学特別講義IV
Jun Makino
平成21年6月15日
![]() であり、元の空間に固定されている。もう一つは
であり、元の空間に固定されている。もう一つは
![]() であり、最初の成分を相対速度
であり、最初の成分を相対速度
![]() に平行にとる。従って、
後者は相手の粒子によって違うわけである。この2つを考えることで、相対速
度の変化をもとの静止系でのテスト粒子の変化に焼き直す。
に平行にとる。従って、
後者は相手の粒子によって違うわけである。この2つを考えることで、相対速
度の変化をもとの静止系でのテスト粒子の変化に焼き直す。
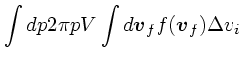
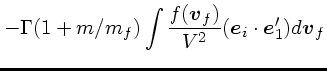
![]() に垂直な成分、す
なわち
に垂直な成分、す
なわち
![]() と
と
![]() の成分を考えればいい。従って、一つの方向から
くるフィールド粒子との散乱を考えた時には
の成分を考えればいい。従って、一つの方向から
くるフィールド粒子との散乱を考えた時には
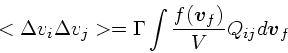
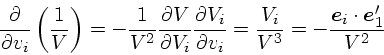
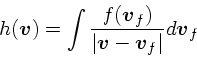
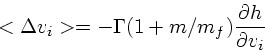
![]() は
は
![]() ,
,
![]() の
の
![]() と
と
![]() によって張られる平面への写像の内積なので、
によって張られる平面への写像の内積なので、
![]() と
の内積の分をつけてやれば元の単位ベクトル同士の内積になる。つまり、
と
の内積の分をつけてやれば元の単位ベクトル同士の内積になる。つまり、
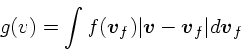
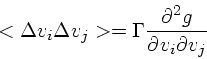
![]() や
や![]() の積分を、
の積分を、
![]() の絶対値方向と角度方
向に分けることができる。角度方向の積分については、
の絶対値方向と角度方
向に分けることができる。角度方向の積分については、
![]() と
と
![]() の
なす角度を
の
なす角度を ![]() とし、
とし、
![]() とすれば、球面上での積分
が、まず
とすれば、球面上での積分
が、まず![]() については
については
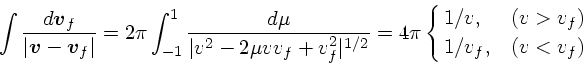
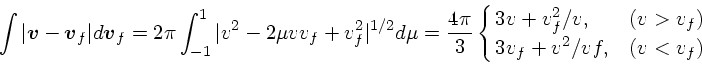
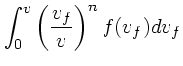

![$\displaystyle {4\pi v^3 \over 3} [3F_2(v) + F_4(v) + 3E_3(v) +E_1(v)]$](img51.png)
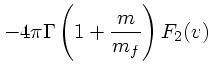
![$\displaystyle {8 \pi \Gamma v \over 3} [F_4(v) + E_1(v)]$](img55.png)
![$\displaystyle {8 \pi \Gamma v \over 3} [3F_2(v)-F_4(v) + 2E_1(v)]$](img57.png)
![\begin{displaymath}
<\Delta E> = 4 \pi \Gamma v\left[E_1(v) -{m \over m_f}F_2(v)\right]
\end{displaymath}](img60.png)
![\begin{displaymath}
<\Delta E^2> = {8 \pi \Gamma v^3 \over 3} \left[F_4(v) +E_1(v)\right]
\end{displaymath}](img62.png)
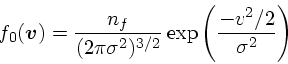
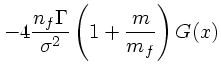
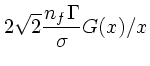
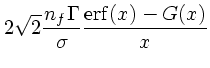
![$\displaystyle \sqrt{2}{n_f \Gamma\over \sigma }\left[-{m \over m_f}{\rm erf}(x)
+ \left( 1 + {m \over m_f}\right)x {\rm erf}'(x)\right]$](img68.png)
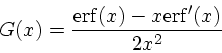
![]() だけ
を通して依存しているということに注目して欲しい。例えば、マックスウェル
分布のようなものを考えた時、
だけ
を通して依存しているということに注目して欲しい。例えば、マックスウェル
分布のようなものを考えた時、 ![]() が大きい極限では
が大きい極限では
![]() となるので、回りが止まっているときと同じく速度変化は速度の2乗に
反比例する。これに対して、
となるので、回りが止まっているときと同じく速度変化は速度の2乗に
反比例する。これに対して、![]() が小さい極限では、
が小さい極限では、![]() を一定と見なすことが
出来るので
を一定と見なすことが
出来るので ![]() となる。
となる。
![]() であるのに対し、逆の極限では 一定になるということであ
る。すなわち、非常に速度が大きい粒子が出来てしまうとこれはなかなか減速
しない。もちろん、自己重力系の場合には、そのようなものは系のなかに留ま
るのが困難だということもあるが。
であるのに対し、逆の極限では 一定になるということであ
る。すなわち、非常に速度が大きい粒子が出来てしまうとこれはなかなか減速
しない。もちろん、自己重力系の場合には、そのようなものは系のなかに留ま
るのが困難だということもあるが。
![]() で決まる値あたりになるということである。
で決まる値あたりになるということである。
![]() が
大きい極限では0にいく。特に、 垂直な成分は
が
大きい極限では0にいく。特に、 垂直な成分は![]() に反比例する。これに対し、
速度が
に反比例する。これに対し、
速度が![]() の極限では、どちらも一定値に収束する。これは停止している極限
でも、回りの粒子によって揺さぶられるということを表しているわけである。
の極限では、どちらも一定値に収束する。これは停止している極限
でも、回りの粒子によって揺さぶられるということを表しているわけである。