ここまでの線形解析は、極めて普通のもの(平衡状態からの摂動の発展の線形 解析)を考えてきた。が、これは歴史的には最初にやられたものではない。 歴史的には、Linear Series Analysis というもうちょっと簡便な方法が使わ れてきた。これは一体どういうものか、を Lynden-Bell and Wood (1968, MNRAS 138, 495) に従ってみていく。 半径、質量一定の平衡形状の系列を考える。 実際に計算するには、等温解をどこか有限の半径で切ったもので、半径、質量 等をスケールしなおせばいい。 とにかく、これで例えば中心と壁のところの密度比 D をパラメータとして系 列がでる。

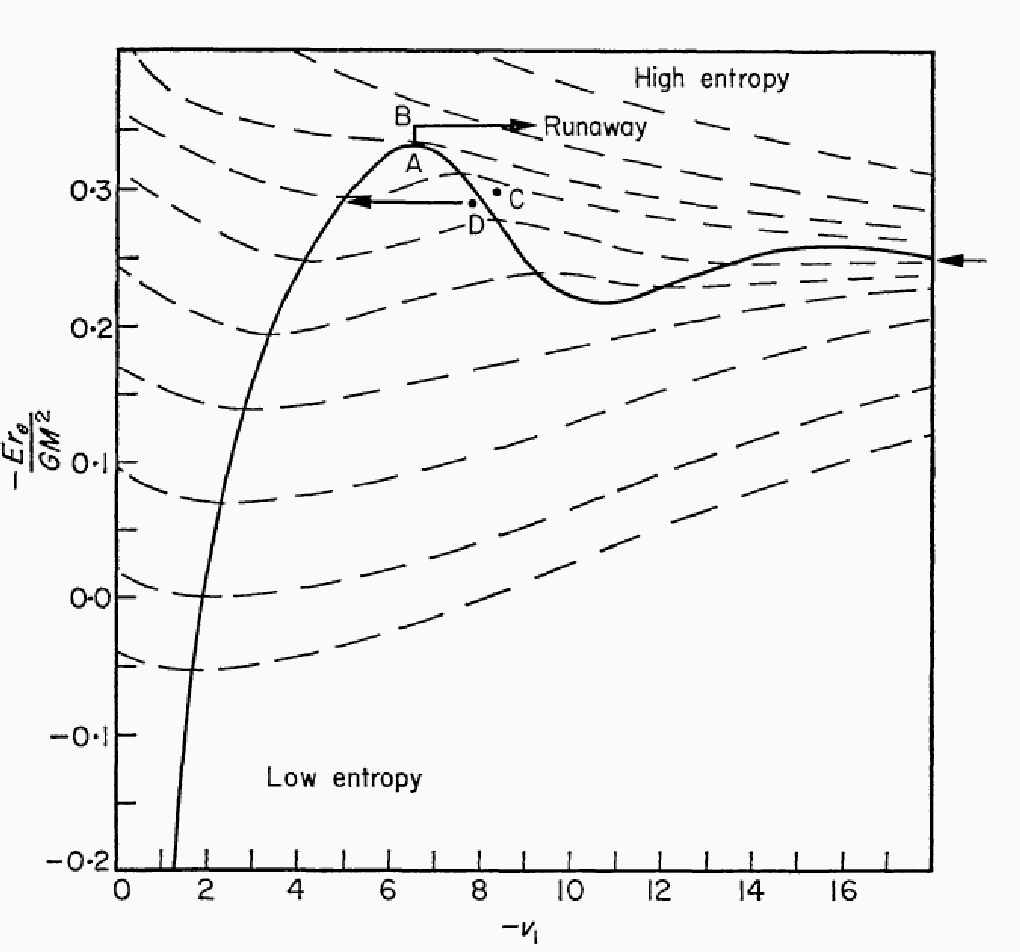
図は、横軸は ![]() 、縦軸はエネルギー(符号逆)を書いたものである。
、縦軸はエネルギー(符号逆)を書いたものである。
![]() でエネルギー極小になり、この点が中立安定点に対応し、それよりも
大きな
でエネルギー極小になり、この点が中立安定点に対応し、それよりも
大きな ![]() では系は熱力学的に不安定である。
では系は熱力学的に不安定である。
何故エネルギー極小が中立安定だったり、そこから先が不安定だったりするの か、というのはあんまり自明ではないと思う。原論文の説明も要領を得ない。
一応、中立安定点には以下のような解釈が可能である。
エネルギー極小点: エネルギーを変えないで(断熱的に) D を(微小量)変えることができる。
つまり、系を等温に保つ摂動で、エントロピーを保存して構造を変えるものが ある。
つまり、中立安定な摂動がある。
中立安定点では、ゼロ固有値に対応する固有関数は温度勾配を作らないものであった。
従って、中立安定点を探すだけなら、摂動を温度勾配を作らないものに制限し てかまわない。
逆に、温度勾配を作らない摂動は、熱平衡状態を熱平衡平衡状態に移すものし かない。
従って、エネルギーを保存して温度勾配を作らない摂動は、エネルギーが極値 を取るところにしかない。
と、これはいいけど、中立安定点より先がどうなってるかは linear series analysis では本当は良くわからない。
固有値問題を解くのと違って、 Linear Series Analysis は平衡系列を求める だけでできちゃうので、いろいろな論文が発生する。
他にもいろいろあるけど、影響が割合大きいものということで。
10 cm
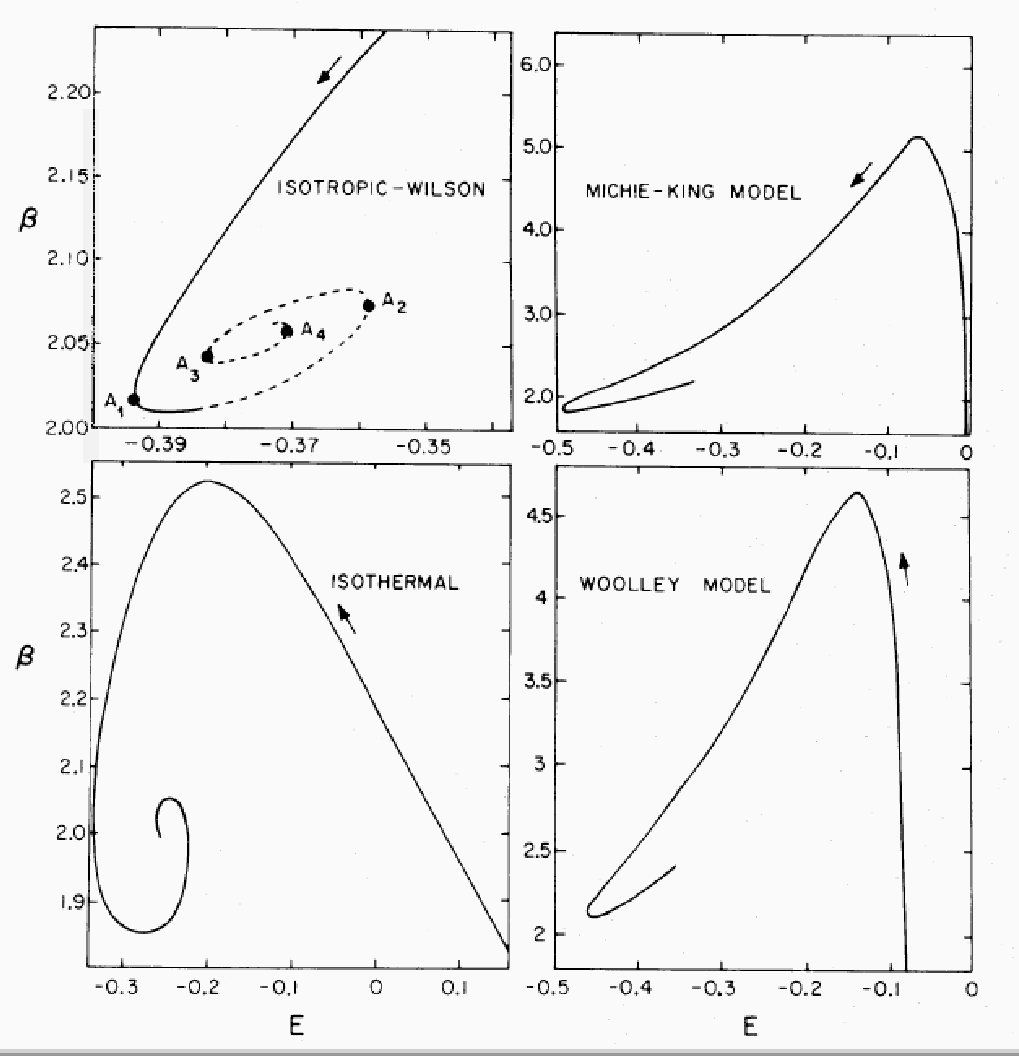
King model の系列に Linear Series Analysis を適用。
「中立安定点」を「発見」( ![]() )
)
もともと等温平衡解ではないもの:
エネルギー一定の摂動が中立安定に対応するわけではない。
断熱壁をつけたポリトロープに同様な解析を適用
11 cm
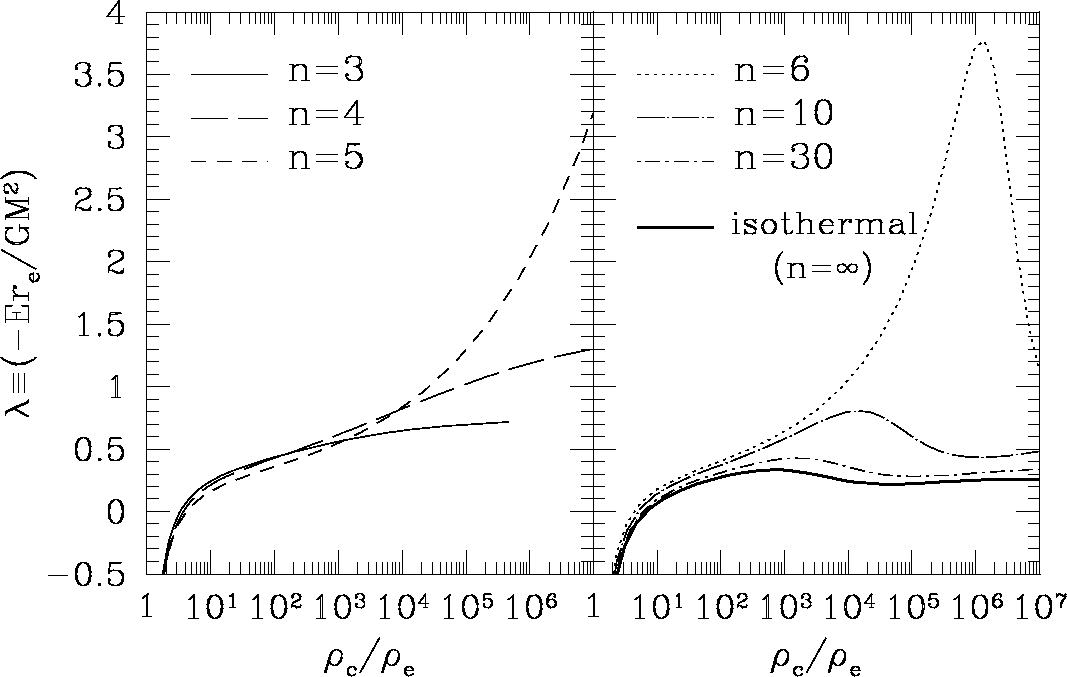
![]() で「不安定性」発見
で「不安定性」発見
実際には彼らは単にポリトロープをなんかしたわけではない。
Tsallis エントロピー ![]()
普通のエントロピー ![]() を
を
![]() の極限として含む、
「一般化された」エントロピー。
の極限として含む、
「一般化された」エントロピー。
これの極値を取る分布 = ポリトロープ( ![]() と
と ![]() は対応する)
は対応する)
そういうものを考える意味: 正直にいって「よくわからない」
Tsallis エントロピー極値は熱平衡であるわけではないので、「安定性」に意 味があるわけではないのは King model の場合と本質的には同じ。