牧野淳一郎
この講義ではこれまで球対称にごく近い系を扱ってきたが、ここからは 少し気分を変えて円盤状の系を扱う。
円盤に近い恒星(とは限らない)系の代表的な例は以下のものである
これらは、円盤である、ということについては同じであり、物理プロセスにも 共通の部分もあるが、違うところもある。大きな違いは、
にある。銀河円盤は重い、つまり、ダークマターハローやバルジの質量と、円盤の
質量は同程度と考えられており、自己重力の効果が大きい。これに対して、
リングでは、例えば土星リングでもその質量は土星本体の ![]() 程度で
ある。原始惑星系円盤では、太陽の質量の 1% 以下と考えられている。
この、質量の違いは、不安定モードやパターンの大きさに違いをもたらす。
程度で
ある。原始惑星系円盤では、太陽の質量の 1% 以下と考えられている。
この、質量の違いは、不安定モードやパターンの大きさに違いをもたらす。
重力ポテンシャルについては、原始惑星系円盤やリングでは(リングの場合には 若干のずれるがあるが)重力場は基本的には中心星のケプラーポテンシャルであ るが、銀河円盤では円盤自身やダークマターハローが作るポテンシャルになっ て単純なケプラーポテンシャルではない。このことは、リングや惑星系円盤の 場合には基本的に軌道は閉じた楕円軌道であるのに対して、銀河円盤ではリサー ジュ図形で閉じない、という違いをもたらす。閉じた軌道の場合には平均運動 共鳴や永年摂動の役割が閉じない場合よりもはるかに大きくなり、ケプラー軌 道であることに固有の様々な現象が起きる。
最後に、物理的な衝突の効果も重要である。惑星リングでは典型的には1つの 粒子は軌道周期程度の時間で他の粒子と衝突する。このため、重力による2体 緩和ではない、物理的衝突による強い緩和が働く。原始惑星系では、2体緩和 と衝突・合体の双方が重要になる。
これに対して、銀河円盤では恒星同士の2体緩和は基本的には無視できると考 えられる。しかし、速度分散(ここでは円運動からのずれをランダム速度と定 義する)については、古い星ほど大きいことが知られており、加熱のメカニズ ムとしてはスパイラルアームとの相互作用の他、分子雲との相互作用も候補 である。つまり、分子雲は質量が大きな粒子とみなせるので、2体緩和を非常 に速くするわけである。
とはいえ、この講義では、まず無衝突系としての安定性を考える。
実際の円盤銀河では、渦巻構造が見えるわけだが、実は渦巻構造の起源はなに かとかなぜ存在できているのか、というのは色々未解決なことが沢山残ってい る問題である。その理由は、基本的には、理論的な安定性解析が解析的にできるのは tight-winding 近似と呼ばれる、渦巻が非常にきつく巻いている、という仮定、 言い換えると、ほぼ軸対称であるという仮定をおける場合だけだからである。
というわけで、まずは軸対称モードの話をする。
式の誘導は結構大変なので、まず流体の場合に結果だけ書く。![]() を半径方向
の波数、
を半径方向
の波数、![]() を時間方向の角振動数、
を時間方向の角振動数、![]() を音速、
を音速、 ![]() を面密
度、
を面密
度、![]() をエピサイクル角振動数として、分散関係が
をエピサイクル角振動数として、分散関係が
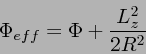 |
(2) |
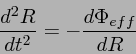 |
(3) |
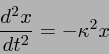 |
(4) |
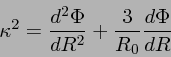 |
(5) |
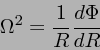 |
(6) |
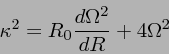 |
(7) |
| (8) |
で、式(1)の意味を考える。まず、
ジーンズ不安定の式と並べてみよう。ジーンズ不安定の分散関係は
| (9) |
| (10) |
最後に、 ![]() の項は、元々の重力ポテンシャル上のエピサイクル運動
そのものである。
音速 0 で自己重力も 0 の極限ではこの項だけになるのでこの形でないといけ
ないことは了解して欲しい。
の項は、元々の重力ポテンシャル上のエピサイクル運動
そのものである。
音速 0 で自己重力も 0 の極限ではこの項だけになるのでこの形でないといけ
ないことは了解して欲しい。
この形からすぐに色々なことがわかる。まず、 ![]() の極限、つまり、温
度
の極限、つまり、温
度 ![]() の極限を考える。そうすると、
の極限を考える。そうすると、
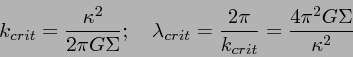 |
(11) |
ジーンズ不安定と違うのは、エピサイクル運動が重力を抑える効果になること と、重力が2次元的で距離が近いと強くなるために、波長が短いと不安定で、 成長速度も波長が短いほど大きい、ということである。
温度0でない、つまり ![]() の場合を考える。あらゆる波数
の場合を考える。あらゆる波数 ![]() に対して
振動数
に対して
振動数 ![]() が実数であるためには
が実数であるためには
| (12) |
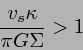 |
(13) |
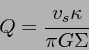 |
(14) |
恒星円盤の場合にも、同じような分散関係から安定性限界を導くことができ、
それは
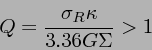 |
(15) |
なお、ここまでの解析は、ディスクが無限に薄いとか、重力場や回転の影響は
ローカルなポテンシャルの微分だけで書けるとか仮定しているので、波長が半
径![]() に比べて十分小さく、なおかつディスクの厚さに比べて十分長い場合に
ついてのみ適用できる。
に比べて十分小さく、なおかつディスクの厚さに比べて十分長い場合に
ついてのみ適用できる。
ディスクが厚さをもっている場合を考えると、十分短い波長では重力が3次元的に
なって普通のジーンズ不安定の表式になる。問題は、
![]() とディ
スクの厚さの関係、ということになる。
とディ
スクの厚さの関係、ということになる。
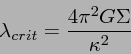 |
(16) |
原始惑星系円盤の場合には、古典的な京都モデルでは、ガスディスクの中でダ
ストが赤道面に沈降していって、厚さが
![]() より小さくなった
あたりで
より小さくなった
あたりで
![]() で決まるくらいの大きさに分裂し、微惑星ができ
る、というシナリオを考える。実際にこのようなことが起こるかどうかについ
ては、ガスディスクが乱流的になるはず、といった議論がありはっきりしない
のが現状である。
で決まるくらいの大きさに分裂し、微惑星ができ
る、というシナリオを考える。実際にこのようなことが起こるかどうかについ
ては、ガスディスクが乱流的になるはず、といった議論がありはっきりしない
のが現状である。
円盤銀河の場合には、面密度は1まではいかないにしても 0.1 より大きい程度
になり、このために
![]() は結構大きい。このため、普通の恒
星円盤では厚さは臨界波長より小さく、 Q 値がそれなりに安定性を表すと思っ
てよい。
は結構大きい。このため、普通の恒
星円盤では厚さは臨界波長より小さく、 Q 値がそれなりに安定性を表すと思っ
てよい。
既に述べた、 tight winding の近似のもとでは、m本腕モードの分散関係は
と書けることが示されている。これは要するに、安定・不安定の条件は ![]() のモードと全く同じで、不安定な時には実部に
のモードと全く同じで、不安定な時には実部に ![]() が入る、言い換え
ると、不安定モードはラグランジュ的に回転にくっついて成長する、というこ
とである。
が入る、言い換え
ると、不安定モードはラグランジュ的に回転にくっついて成長する、というこ
とである。
これは、 tight-winding 近似してさらに半径方向に対して波長が短いという
近似もしたので、 ![]() の半径依存性もどこかで落として解析したような
話になっている。
の半径依存性もどこかで落として解析したような
話になっている。
実際の銀河では、全く tight-winding も局所近似も成り立たないような大き なスケールでのスパイラル構造が見つかっている。 例えば以下は Spitzer 衛 星で観測した M101 のイメージである。
10 cm

中間赤外で見える低温のガスは複雑な構造をもつが、大きなスケールでのスパ イラルアームがあるように見える。これは、多くの銀河についてそういう構造 があるように見える。
しかし、そのような構造を定常的に維持するメカニズムはなにか、それ以前に そもそもそのようなメカニズムはあるのか、ということは、依然未解決の問題 である。これは、上の解析のように不安定モードは基本的にローカルな角速度 で回転するため、半径方向に広がったモードはどうしても差動回転の効果で時 間がたつと巻き込んでしまうことになり、ある形をもったスパイラルアームが 時間的に成長したり、定常状態になったりしてくれないからである。
これまで唱えられていた理論は例えば以下のようなものがある
=8cm
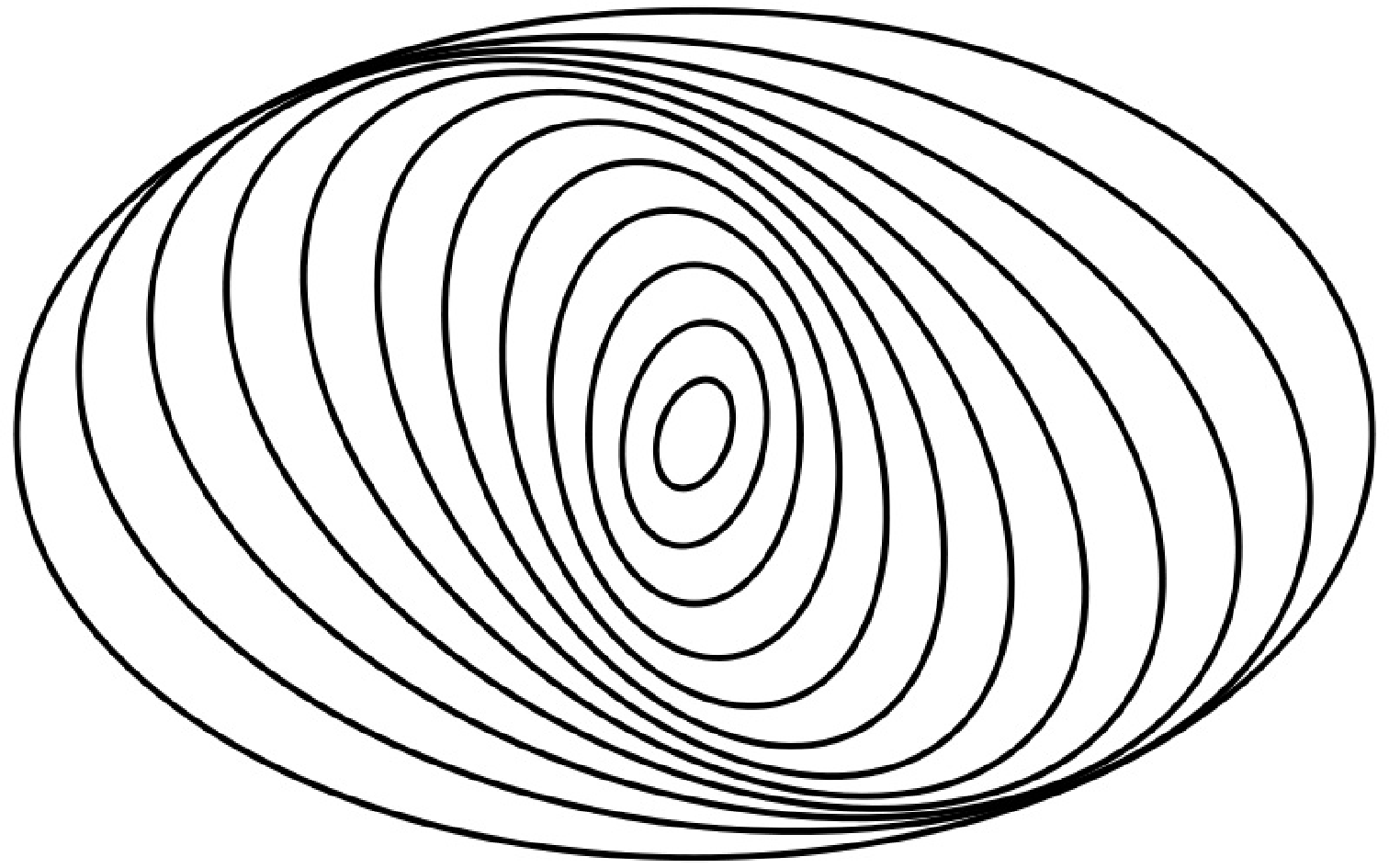
こんな感じにうまいこと軌道がずれていくことでできる見かけのパターンであ るとするものである。そうはいってもエピサイクル周期も半径に依存するし、 なぜ同じ半径では大体位相がそろうのかとか、うまいことスパイラルパターン がでるようにその位相が半径によってずれるのかとかは良くわからない。
90年代以降この辺はあまり研究されていなかったが、 最近の大粒子数での数値計算(Fujii et al, in preparation)では、初期の Q の値や粒子数によっては、ガスによる冷却効果がなくても非常に長い時間にわ たって非定常なスパイラル構造が見える、ということがわかってきた。
上で述べたような、非定常な構造の進化を考える上で有用な概念の一つが swing amplification である。現象としては、これは、以下の図に示すようなことが起こる、というものである。
=10cm
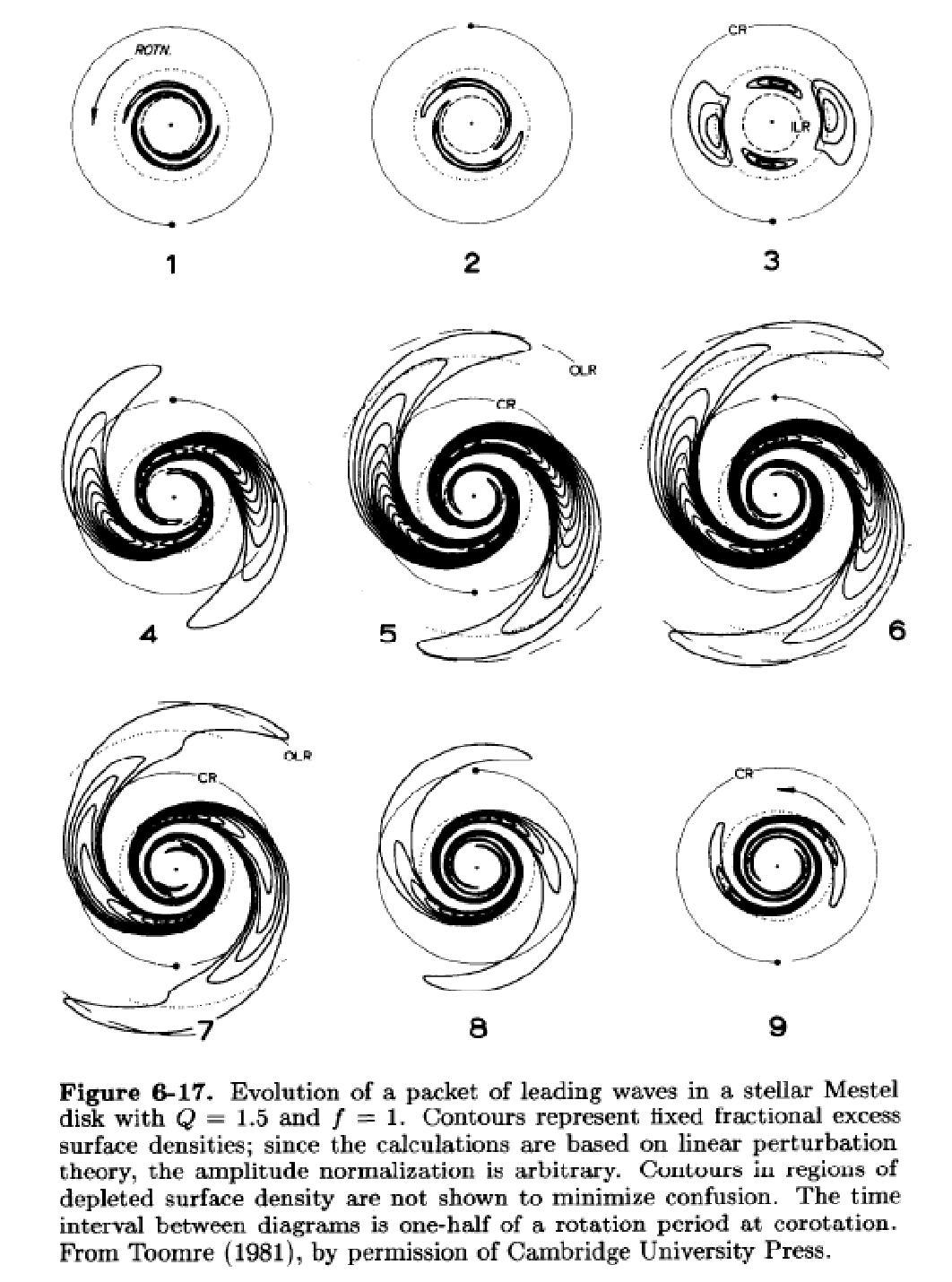
最初に leading arm (外側のほうが先に進んでいる)な摂動を与えると、これ が最初は巻き込みがほどけていってそのうちに trailing に変化する。その間 に、 trailing で非常に振幅の大きなアームが一時的に見える。これは、 単純にいってしまうと、 leading から trailing に変化する最中だと、モー ドの回転とエピサイクル運動の回転が同じ向きで、このために回転の効果がキャ ンセルされて普通のジーンズ不安定に近い状況になって摂動がどんどん成長で きる、というような話である。
=10cm
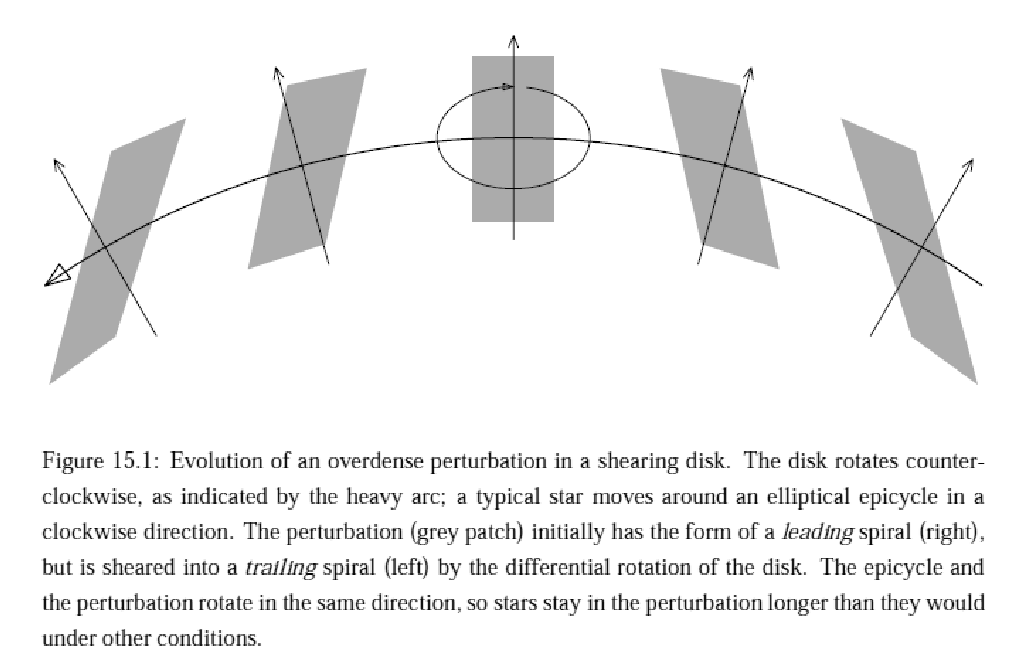
但し、これが機能するためにはどこからか leading arm な摂動が供給されなけ
ればならない。![]() 体計算では、最初にランダムに粒子を置くと、ポアソンゆら
ぎからアームが成長していくが、単純にポアソンゆらぎからの成長で、一回切
りの現象だと思うと粒子数を増やせばアーム強度は小さくなるはずである。ま
た、成長時間も粒子数に依存しないはずである。しかし、数値計算の結果は、
最大のアーム強度は粒子数に依存せず、また成長は粒子数が大きいと遅い、と
いうことを示唆している。
体計算では、最初にランダムに粒子を置くと、ポアソンゆら
ぎからアームが成長していくが、単純にポアソンゆらぎからの成長で、一回切
りの現象だと思うと粒子数を増やせばアーム強度は小さくなるはずである。ま
た、成長時間も粒子数に依存しないはずである。しかし、数値計算の結果は、
最大のアーム強度は粒子数に依存せず、また成長は粒子数が大きいと遅い、と
いうことを示唆している。
上でみたように、スパイラル構造についてはそれを定常的に維持するメカニズ ムが何か、そもそもそんなものがあるのか、ということが良くわかっていない。
しかし、グローバルな非軸対称モードとしてはスパイラルの他にバー不安定が あり、これについては非線型領域で定常なバー構造が存在できることは古くか らわかっている。 Q値的には安定なディスクであっても、ディスクだけでダー クマターハローやバルジがないと必ずバー不安定を起こす、ということが 1970年代から知られている。但し、グローバルモードであることから安定性条 件等が単純な形で得られているわけではない。
バーがある場合にはその外側には2本腕のスパイラルができ、これは基本的に は密度波的な構造であると考えられている。
cm
図に VLBI での位置天文的な観測例を示す。これは、 VLBI (超長基線干渉計)で遠くの星の距離と動く速度を三角測量で決めたもの である。 データのほとんどは アメリカの VLBA によるものである。
10cm
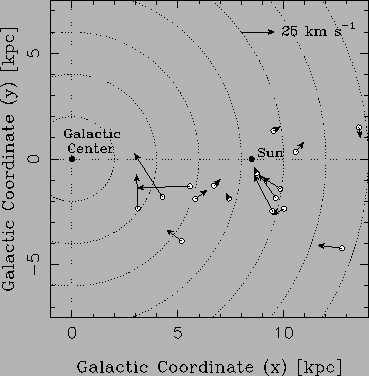
ちなみに、日本では国立天文台の VERA で同様な観測を進めているはずである。
14cm
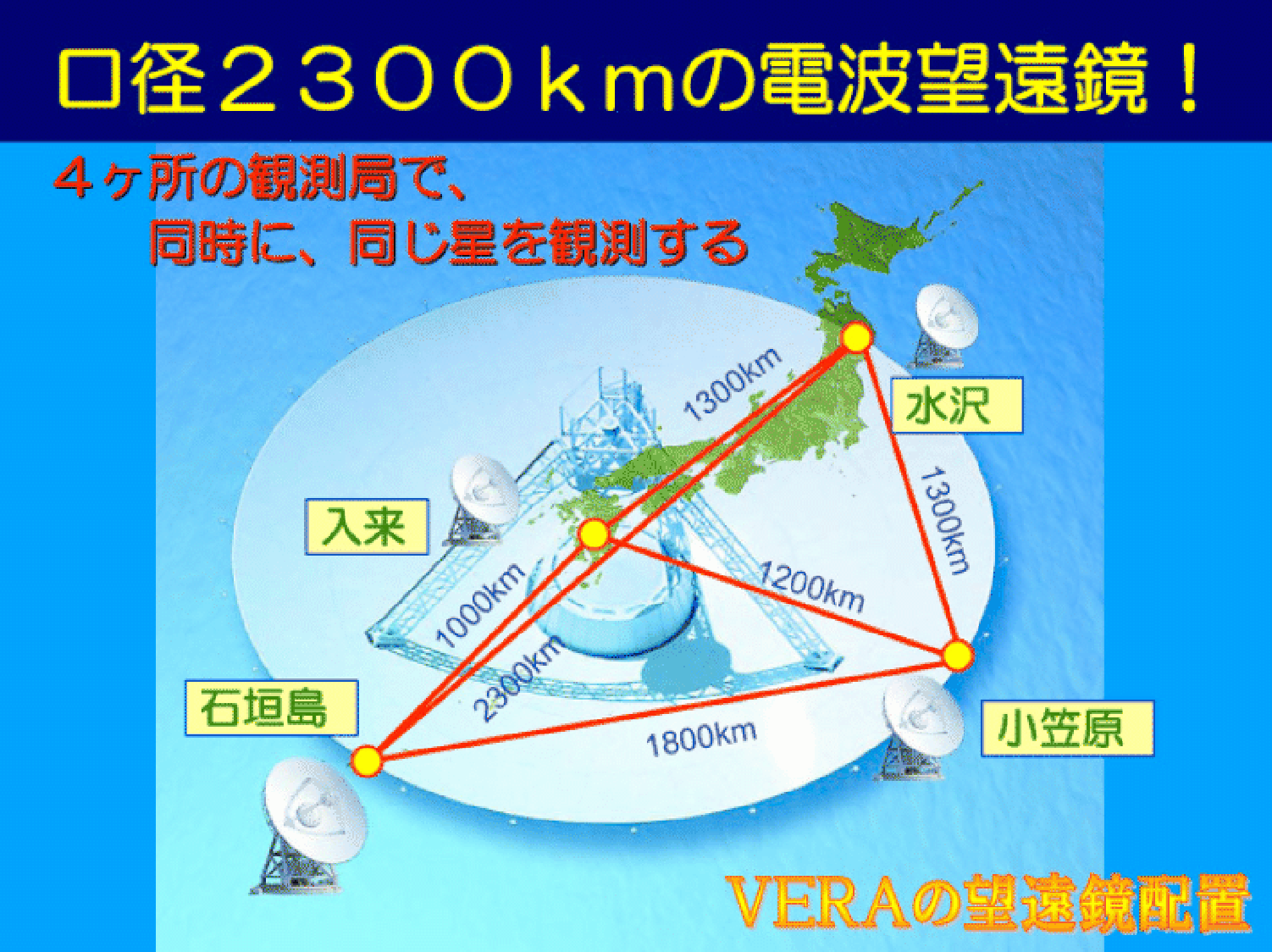
なお、これは、とても大変な観測である。
観測からいえそうなこと:
(馬場他 2009)
animation /home/makino/WWW/tmp/movies/disk_simulation_combine.wmv1 /home/makino/papers/cfca/babadata/baba/anime2.mov2 )
空間構造と、円運動からのずれ
![\includegraphics[width=14cm,angle=0]{/home/makino/papers/Takayuki_Saitoh/book/PetaCom/PeculiarVelocityMap2501Makino1_200.eps}](img49.png)
左:星の分布 右: 冷たい星間ガス
| 6cm |
| 6cm |
| 6cm |
| 6cm |
昔の計算
最近の計算
数値計算法の色々な改良(というか、原理的に問題があったところの修正等)で可 能になった。
(藤井他 2010)
/home/makino/tmp/anime_a1.gif Animation a1
/home/makino/tmp/anime_a2.gif Animation a2
/home/makino/tmp/anime_b1.gif Animation b1
講義で取り上げた論文のどれか1つを読み、その内容を要約し、 そこでの主張について妥当性を検討せよ。 複数の論文についてレポートを出し てくれればそれなりに評価を上げる。
レポート〆切: 10/31
レポート提出先: makino あっと geo.titech.ac.jp に PDF ファイルをメイルで送る こと。
この文書はLaTeX2HTML 翻訳プログラム Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds,
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
を日本語化したもの( 2002-2-1 (1.71) JA patch-1.9 版)
Copyright © 1998, 1999, Kenshi Muto, Debian Project.
Copyright © 2000, Jun Nishii, Project Vine.
Copyright © 2001, 2002, Shige TAKENO, Niigata Inst.Tech.
Copyright © 2002, KOBAYASHI R. Taizo, Project Vine.
を用いて生成されました。
コマンド行は以下の通りでした。:
latex2html -nomath_parsing -local_icons -show_section_numbers -split 0 note11-e.tex.
翻訳は Jun Makino によって 平成24年10月2日 に実行されました。