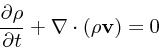 |
(1) |
牧野淳一郎
ここまで、自己重力多体系の平衡形状を(ごく簡単な場合だけ)扱ってきたが、 ここからしばらくは平衡形状ではなく時間発 展について考えることにしたい。
時間発展といっても、もとの方程式が強い非線形性を(加速度の項に)持つの で、一般的な場合を解析的に扱うことはほとんど出来ない。そこで、ま ず、平衡状態から無限小だけずれている場合に対して線形化した発展を考える ということにする。さらに、話を簡単にするために、「無限一様」な平衡状態 とし、まず無衝突ボルツマン方程式ではなく流体の話を考える。
流体は、連続の式
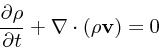 |
(1) |
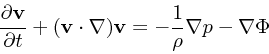 |
(2) |
| (3) |
今、
![]() をそれぞれ
をそれぞれ
![]() という格好にして、添字 0 がつくものはもとの方程式の平衡解であ
り、
という格好にして、添字 0 がつくものはもとの方程式の平衡解であ
り、 ![]() がつくものは小さい(二次以上の項を無視していい)として方程式を
書き直すと
がつくものは小さい(二次以上の項を無視していい)として方程式を
書き直すと
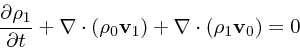 |
(4) |
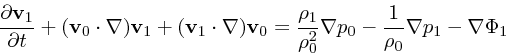 |
(5) |
| (6) |
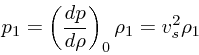 |
(7) |
既に述べたように、無限一様でいたるところ密度、圧力が等しいというのが平
衡で、速度も0だったとすると、上の2本は
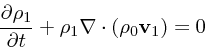 |
(8) |
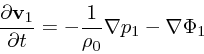 |
(9) |
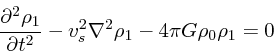 |
(10) |
最初の2項をみれば普通の波動方程式で、最後の項がポアソン方程式を通して でてくる重力の項である。したがって、波長が短い極限では普通の波動方程式 に近付く。これに対し、波長が長い極限では空間2階微分の項が効かなくなる ので、線形の常微分方程式になってしまう。
実際に分散関係を求めるために、解を
| (12) |
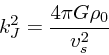 |
(13) |
なお、一応念のために書いておくと、式(11)の形の解だけを 考えるのは任意の初期条件からの解が(連続性とかを仮定すれば)この形の解 の線形結合で表現できるからである。解の線形結合が解であるのは方程式が線 形だからであり、任意の解が表現できるのは要するにフーリエ変換が完全系を なすからである。
話を戻すと、定性的に見たときにわかったように、波長が短ければ普通の音波
として振舞うが、波長が ![]() より長いと時間の指数関数で進化すること
になる。つまり、密度が上がり始めたらどんどんあがる(下がり始めたらどん
どんさがる)ということになる。
より長いと時間の指数関数で進化すること
になる。つまり、密度が上がり始めたらどんどんあがる(下がり始めたらどん
どんさがる)ということになる。
ここで注意して欲しいのは、十分に波長が長いと必ず不安定になるということ である。これはつまり、重力があると無限に一様な状態というのは温度無限大 でない限り必ず不安定であるということである。
さて、 ![]() というのは直観的にはどういうものかというのを考えてみる。
というのは直観的にはどういうものかというのを考えてみる。
![]() は波数なので、その逆数に
は波数なので、その逆数に ![]() を掛けると波長になる。これをジー
ンズ波長
を掛けると波長になる。これをジー
ンズ波長 ![]() といって、式にすると
といって、式にすると
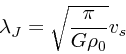 |
(14) |
今、半径がジーンズ波長くらいの球を考えてみる。これの単位質量当りの運動
エネルギー(熱エネルギー)は、もちろん ![]() の程度である。これに対し
て重力エネルギーは
の程度である。これに対し
て重力エネルギーは
![]() の程度、ここで
の程度、ここで ![]() はジーンズ質
量で半径
はジーンズ質
量で半径 ![]() の球の質量である。
の球の質量である。 ![]() に上の式を入れて計算すると、結局
重力エネルギーが定数を別にして
に上の式を入れて計算すると、結局
重力エネルギーが定数を別にして ![]() の程度になることがわかる。
の程度になることがわかる。
つまり、熱エネルギーより重力エネルギーが大きくなるような長さの摂動は成 長するということになる。
恒星系の場合を考えることにしよう。
何度も出てきたがもう一回式を書いておく。
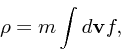 |
(17) |
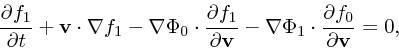 |
(18) |
 |
(19) |
上の線形化されたボルツマン方程式は、平衡解の回りならば何でも使えるが、
ここではもっとも簡単に解析できる場合として空間分布が一様な場合を考える。
これから ![]() は速度だけの関数であり、
は速度だけの関数であり、 ![]() は定数としていいことに
なるので
は定数としていいことに
なるので
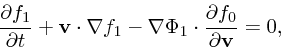 |
(20) |
| (21) | |||
| (22) |
 |
(23) |
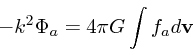 |
(24) |
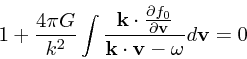 |
(25) |
もっとも、これはちょっと困った式で、
![]() が特
異点になっている。したがって、実数の振動数を考えるのはすこし厄介な話に
なる。まず、臨界点、すなわち振動数が
が特
異点になっている。したがって、実数の振動数を考えるのはすこし厄介な話に
なる。まず、臨界点、すなわち振動数が ![]() の場合と、不安定、すなわち振動
数が純虚数の場合を考えよう。
の場合と、不安定、すなわち振動
数が純虚数の場合を考えよう。
式が繁雑なので、いま、
波数ベクトルを![]() 軸方向にとることにすると、分散
関係は
軸方向にとることにすると、分散
関係は
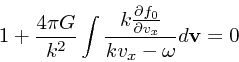 |
(26) |
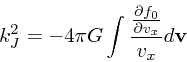 |
(27) |
流体の場合と対応をつけるために、速度分布 ![]() をマックスウェル分布
をマックスウェル分布
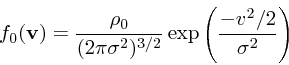 |
(28) |
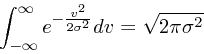 |
(29) |
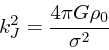 |
(30) |
次に、振動数が純虚数の場合を考えてみる。この時は、
![]() として元の式にマックスウェ
ル分布を入れて整理すると
として元の式にマックスウェ
ル分布を入れて整理すると
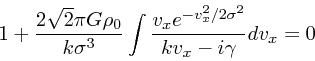 |
(31) |
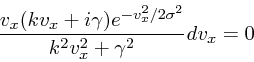 |
(32) |
![\begin{displaymath}
\int_0^{\infty} {x^2 e^{-x^2} \over x^2 + \beta^2} dx =
{ 1 ...
...rt{\pi} - {1 \over 2} \pi\beta
e^{\beta^2}[1-{\rm erf}(\beta)]
\end{displaymath}](img69.png) |
(33) |
![\begin{displaymath}
k^2 = k_J^2\left\{ 1- {\sqrt{\pi}\gamma \over \sqrt{2}k\sigm...
...rf}\left({\gamma
\over \sqrt{2}k\sigma}\right)\right]\right\}
\end{displaymath}](img70.png) |
(34) |
というわけで、波長がジーンズ波長よりも長いモードは流体と同様不安定で、 勝手に成長することになる。
さて、それでは、音波に当たるような振動数が純実数のモードというものはあ
るのだろうか?これについては、 BT を含めて標準的な教科書でも若干混乱し
た記述がなされていることがある。以下、 van Kampen の論文 (1955,
Physica, 21, 949) に沿った理解を試みることにする。分散関係の一つ前の式
に戻ってみると、
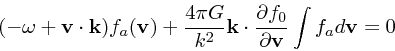 |
(35) |
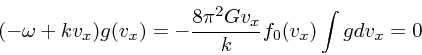 |
(36) |
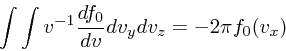 |
(37) |
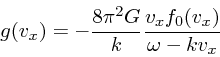 |
(38) |
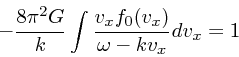 |
(39) |
最初にもいったように、この式がよろしくないのは ![]() で積分が
特異になるからである。意味のある解を求める一つの考え方は、
で積分が
特異になるからである。意味のある解を求める一つの考え方は、 ![]() を超関数
に拡張してしまうことである:
を超関数
に拡張してしまうことである:
![\begin{displaymath}
g(v_x) = -{8 \pi^2 G v_x f_0(v_x)\over k}\left[{\cal P}{ 1\over \omega
- kv_x} + \lambda\delta(\omega - kv_x)\right]
\end{displaymath}](img83.png) |
(40) |
これがいったいどういうものかを少し考えてみよう。まず、 ![]() 関数の
分は、
関数の
分は、
![]() のところにだけ値があるということを示している。
つまり、位相速度が摂動を受けていないもともとの速度と等しい、いいかえれ
ば与えたものがそのままラグランジュ的に動いていくようなものである。これ
は、いま重力がまったくない極限を考えれば、単に摂動がまわりと相互作用す
ることなくそのまま動いていくというものであると考えられる。これにたいし
て、もう一つの項は重力による応答を示していると考えていい。
のところにだけ値があるということを示している。
つまり、位相速度が摂動を受けていないもともとの速度と等しい、いいかえれ
ば与えたものがそのままラグランジュ的に動いていくようなものである。これ
は、いま重力がまったくない極限を考えれば、単に摂動がまわりと相互作用す
ることなくそのまま動いていくというものであると考えられる。これにたいし
て、もう一つの項は重力による応答を示していると考えていい。
このへんはちょっとお話しになって申し訳ない(詳細を知りたいひとは van Kampen の原論文に当たってほしい)が、 van Kampen モードは完備であるこ とがわかっている。つまり、任意の摂動をvan Kampen mode の組合せとして表 現できる。
さて、任意の摂動が、減衰しないモードの組合せとして表現できるのなら、そ れはなにか音波のような伝わっていく波になっているのであろうか?実はそん なことはない。これは、以下の簡単な例で示すことができる。1次元で、重力 がない系である有界な領域に摂動(overdensity)を与えたとする。で、簡単の ために周期境界で、右から出ていったものが左から入ってくるとしよう。もち ろん、ちゃんと適当なポテンシャルを考えるとか、無限一様な場合を考えると かしても本質は同じである。(無限一様な場合は、単に周期的な摂動を与えた というのに対応する)
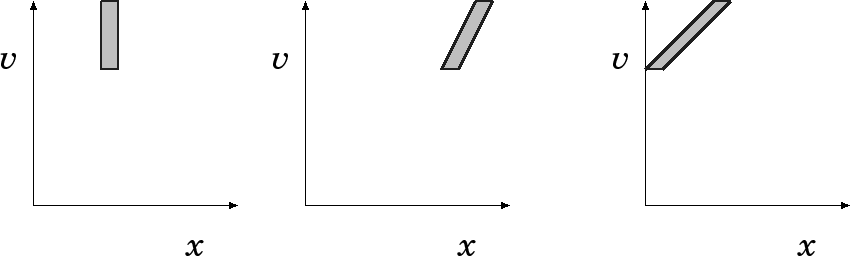
すると、時間がたつに従って摂動が引き延ばされていくということがわかる。 このために、例えば密度の変化といった量は時間がたつにしたがって減衰して いく。
つまり、 singular な van Kampen mode 自体は減衰しないが、それを重ね合 わせた有限の広がりを持つ摂動は減衰するように見える。これが通常 phase mixing と呼ばれるものである。
さて、モードがあって、世の中はその重ね合わせであるというのなら、それで
話はおしまいではないかとおもうのが人情だが、普通はそういう話にはなって
いない。というのは、 Landau Damping という難しいものがあるということに
なっているからである。これはどういう原理ででてくるかというと、要するに
複素数の ![]() があると信じて、そういう解を求めると、ちゃんとそうい
うものが見つかるというものである。つまり、摂動の速度方向の分布
があると信じて、そういう解を求めると、ちゃんとそうい
うものが見つかるというものである。つまり、摂動の速度方向の分布 ![]() を
うまくとってやると指数関数的に減衰するモードがでてくる。ただし、注意し
て欲しいのは、これは、
を
うまくとってやると指数関数的に減衰するモードがでてくる。ただし、注意し
て欲しいのは、これは、 ![]() に制限をつけないと出てこないということであ
る。不連続な
に制限をつけないと出てこないということであ
る。不連続な ![]() を仮定すれば、時間のベキでしか減衰しないような解を構
成することも出来る。ただし、そういった解はモードの形、つまり位置、時刻
の指数関数の形に単純に書けるとは限らない。
を仮定すれば、時間のベキでしか減衰しないような解を構
成することも出来る。ただし、そういった解はモードの形、つまり位置、時刻
の指数関数の形に単純に書けるとは限らない。
逆にいえば、解が指数関数の形に書けると仮定すれば、ジーンズ波長より短け ればそれは指数関数的に減衰するわけである。
今、簡単のために重力がない一次元系を考える。この時 van Kampen mode は
単なる ![]() 関数なので、初期の波数が
関数なので、初期の波数が ![]() であるような摂動は
であるような摂動は
| (41) |
しかし、注意して欲しいのは、これは最初に安定性解析の時に仮定した
![]() という形とは違うということである。これは、
振動数
という形とは違うということである。これは、
振動数 ![]() が
が ![]() そのものであり、速度空間のなかでの位置に依存する
ためである。
そのものであり、速度空間のなかでの位置に依存する
ためである。
このことをいいかえると、上のような「自然な」解があるにもかかわらず、 モード解析をするとvan Kampen mode のような singular なものが出てくるの は、モード解析の仮定として位相速度が粒子の速度に寄らないようなものを考 えたからであるともいえる。
さて、上の「自然な」解はどのように振舞うかをちょっと見てみよう。
密度は、
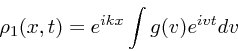 |
(42) |
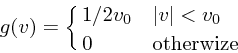 |
(43) |
このような減衰が起きるのは、初期条件が非常に特別なものであるためである ということに注意してほしい。つまり、速度ごとに波の位相速度が違うのに、 初期条件としてその空間位相がすべてそろったものを考えたわけである。そう すると、時間がたてば位相はずれていくので速度方向に積分して見た波の振幅 は小さくなってくことになる。これは、速度方向の「波数」に時間が生で入っ てくるためである。
なお、 ![]() に適当な形を仮定すれば、もっと速く減衰するものも作れる。
に適当な形を仮定すれば、もっと速く減衰するものも作れる。
もちろん、無衝突ボルツマン方程式にしたがった進化は可逆過程である(エン トロピーを生成しない)ので、原理的には逆に振幅が大きくなるような初期条 件も存在していないといけない。実際、減衰していく解で、どこかで時間反転 すればそういう解が作れるわけである。
なお、今日の話で要領を得ないと思った人は、、、この辺は基本的で大事な問 題であるわりにはあまり良いテキストも論文もないので、なかなか難しい。
来週は、粗視化エントロピーの概念を導入し、いわゆる violent relaxation 「激しい緩和」といわれるものの性質について考える。で、Phase mixing の意味ももう一度考え直してみる。
この文書はLaTeX2HTML 翻訳プログラム Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds,
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
を日本語化したもの( 2002-2-1 (1.71) JA patch-1.9 版)
Copyright © 1998, 1999, Kenshi Muto, Debian Project.
Copyright © 2000, Jun Nishii, Project Vine.
Copyright © 2001, 2002, Shige TAKENO, Niigata Inst.Tech.
Copyright © 2002, KOBAYASHI R. Taizo, Project Vine.
を用いて生成されました。
コマンド行は以下の通りでした。:
latex2html -nomath_parsing -local_icons -show_section_numbers -split 0 note4-e.tex.
翻訳は Jun Makino によって 平成24年9月30日 に実行されました。