牧野淳一郎
前回は、Violent relaxation の結果として自己重力系の外側(virial radius のずっと外側)については、
というような話をした。
さて、それでは、中心部の構造についてはなにもいえないのであろうか?これ は実はまだ良くわかっていない問題である。10年前に、 Navarro たち (ApJ 1997, 490, 493) は、数値計算の結果をもとに以下のような主張をした
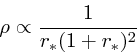 |
(1) |
これは、極めて有名になった NFW プロファイルである。
彼らはなぜそのようなことが起きるかについての解釈とか説明は特に与 えていないが、例えば Syer and White (MN 1998, 293, 337)といった人 達が説明を考えてはいる。
しかし、実は、Navarro たちの結果の解釈は割合すぐに異論がでて おり、 CDM と初期条件を制限しても、例えば Fukushige and Makino (ApJ 1997, 477 L9) とか Moore et al. (ApJ 1998, 499, 5L) を見ると、 上の「ユニバーサル」な形になったのは数値誤差のせいという主張が なされている。これらの結果では Navarro たちのも のより中心で等温に近くなっている。 Navarro らの結果は 1 万粒子程度であ るが、 Fukushige ら、 Moore らは 100 万粒子程度であり、数値誤差の影響 が小さくなっていることは間違いない。「真の」のスロープがどうなるかにつ いては現在も活発な研究が続いているが、現時点では、CDM からの数値 実験でできるハローの中心部は NFW よりもスロープの傾きが大きいというこ とはほぼ万人の認めるところになったようである。
全く余談であるが、福重君はこの仕事とその続きで天文学会研究奨励賞をもらっ た。
さらにもっと余談であるが、福重君がこの計算をした動機は、1996年に GRAPE-4 を使って何か大きな計算で高い実効性能を出したい(Gordon Bell Prize に応募したい)、そのためにはとにかく粒子数が沢山必要で、普通の treecode とかではできないようなシミュレーションでよいネタがないか?と か色々考えたことである。
つまり、現状では、中心部(というか、 half mass radius より内側)の構造は、
という状況であるといえる。現在では、福重君の仕事からさらに 3 桁程度粒
子数を増やした、 ![]() 粒子程度の計算も行われているが、中心部の構造が
どうなるか、それは何故か、というのは依然明確にはなっていない。
粒子程度の計算も行われているが、中心部の構造が
どうなるか、それは何故か、というのは依然明確にはなっていない。
図は、現時点で最大粒子数、最高分解能の計算: Springel et al (2008) であ る。これは粒子数を3桁程度の範囲で変えて、5個のシミュレーションをしてお り、分解能が高い計算は低い計算の、計算が信用できそうな範囲は再現してい る。そういう意味では、計算結果は収束していて、求まっている答はそれなり に正しいと考えられる。
粒子数が少ないと中心のほうが信用できなくなるのは、熱力学的な緩和のため。 これはまた後でもう少し詳しく。
こちらは密度勾配をグラフにしたもの。計算の範囲では中心にいくに従って浅 くなっていて、いかなるべきでもない。
これは Navarro et al. 2008. 傾向は同じで、中心にいくに従って密度勾配が 浅くなっている。
NFW:
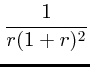
Moore99:
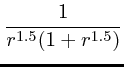
Einasto:
![]()
現在わかっていることをまとめると
というような感じになる。数値計算の結果を疑うわけではないが、何故そうなっ ているかは今のところ全く理解されていない。感覚的には
ので、何かべき乗則になりそうな気がする。
つまり、 数値計算の結果はあっても、それを理解できる理屈がついてない、というのが 現状での大きな問題点である。
数値計算の結果が理論的になにかしら理解できない時には、それが「正しい」 かどうかは判断のしようがない。
もっとも、こんなところの計算にはそもそも意味があるのか?という疑問はある。 銀河サイズのダークマターハローの中心 1 kpc 以内の構造に、観測的になん か意味はあるのか?ということである。 もちろん、これには2つの回答がありえる。一つは「ない」というもので、 その理由は少なくとも実際にの銀河ではその辺は どうせバリオンの影響のほうが大きいからである。もうひとつは、 「ある」というもので、もっと小さい、バリオンをトラップしてない本当にダー クなハロー ならもちろんこのようなものは残っているはずである。
ダークマターを「見る」可能性として、
といった話があり、こういうことを考える時には小さい質量のダークマターハ ローの構造は重要である。原理的には、小さなものが生き残っていて太陽近傍 にある、といった可能性も考慮する必要がある。
小さなハローの構造を考える、という時には明らかに問題なことは、
宇宙論的 ![]() 体シミュレーションは、「無衝突系」の正しいシミュレーション
になっていないことである。
体シミュレーションは、「無衝突系」の正しいシミュレーション
になっていないことである。
宇宙論的 N 体シミュレーションでは、以下のようにして初期条件を作る。
図にすると
=8cm
というような感じ。実際のパワーは何十桁か先まで続いているが、粒子数の限 界があるのでどこかで打ち切る。それよりちょっと低い波数でゆらぎも打ち切 る。
で、コールドダークマターだと、小さいものが先にできる。このため、シミュレーションで最初にできる「ハロー」は粒子10個程度と非常に小さい。ここで、 (私を含む)業界の信念は、階層的な合体成長のプロセスが構造を決めているので、 最小の構造がちゃんと計算できているかどうかは結果に影響しないはず、とい うものだが、これは検証されたことはない。また、ダークマター検出に関係す るような最小スケールのハローではこの信念は明らかに間違っている。
最小ハローがどれくらいの大きさかは、大体地球質量くらいと考えられている。 これは、ダークマターがいつ他のものからデカップルして、自由に動くように なるかできまるが、現在好まれているダークマター粒子のモデルでは地球質量 くらい。サイズは 100 AU くらいになる。そうすると、
というのが問題。
=6.8cm
といってもほとんどこれだけ: Diemand et al. 2005, Nature 433, 389。
基本的に普通の宇宙論的シミュレーションで、
地球スケールのハローを ![]() 粒子くらいで分解している。密度構造を議論
するには粒子数不足。
粒子くらいで分解している。密度構造を議論
するには粒子数不足。
=8cm
Ishiyama et al. 2009 の計算
初期条件の考えかたは以下のようなもの。
=15cm
通常の宇宙論的シミュレーションでは、実際にはずっと先にあるカットオフと は別に、ずっと質量が大きいところで質量分解能の限界がくる。そのちょっと 手前でカットオフを入れる。
Ishiyama et al. の計算では、物理的なカットオフを入れる。それをちゃんと 表現するため、粒子の質量はそこに十分沢山の粒子が入る程度に小さくする。
Diemand et al. の 100倍の粒子数を使った大規模計算。
=8cm
ハローだけの拡大が以下もの
| With cutoff =7.7cm |
| Without =7.7cm |
密度プロファイルを以下に示す。
=8cm
実線がカットオフあり、波線がカットオフなしのもの。カットオフがあるほう
が中心密度が高くなる。ほぼ ![]() のべきで直線でのびているように見える。
カットオフなしだと銀河スケールと同様に、中心にむかって浅くなる。
のべきで直線でのびているように見える。
カットオフなしだと銀河スケールと同様に、中心にむかって浅くなる。
つまり、最小サイズのダークハローは
![]() と書けるよ
うな深いべきの密度構造を持ち、中心密度が高いと考えられる。
と書けるよ
うな深いべきの密度構造を持ち、中心密度が高いと考えられる。
これは、特に対消滅によるガンマ線輻射には大きな影響がある。 ガンマ線輻射率が密度の二乗に比例するので、フラックスが中心にむけて 対数的に発散するからである。
そうすると、
が問題である。とはいえ、なぜ ![]() かはまだあまり理解が進んでいない。
密度の上限については、いわゆる ``pha space argument'' を考えてみる。
これは、無衝突ボルツマン方程式が6次元位相空間での非圧縮流れを与える、
ということを使う議論である。
かはまだあまり理解が進んでいない。
密度の上限については、いわゆる ``pha space argument'' を考えてみる。
これは、無衝突ボルツマン方程式が6次元位相空間での非圧縮流れを与える、
ということを使う議論である。
色々な仮定すると、初期の位相空間密度が
![]() というのがでてくる。これくらいになったところで
密度一定のコアができると思うと、
というのがでてくる。これくらいになったところで
密度一定のコアができると思うと、
このようなハローが現在まで生き残っているかどうかを調べるため、 主要な破壊メカニズムと考えられる恒星との衝突をシミュレーションしてみた。
=5cm =5cm =5cm
=5cm =5cm
衝突後の密度プロファイルを図に示す。
=10cm
非常に近くを通った場合でも中心の高密度領域は簡単には壊れない。完全に壊
すためにはインパクトパラメータが
![]() 以下でないといけないとわかった。
以下でないといけないとわかった。
これは宇宙年齢程度では普通起きない(太陽系もこんなのがあると破壊される)
太陽近傍のハローが生き残っているとすると、
まあ、残念ながら Fermi で見つかった気配はなさそう。
現在、「京」を使って、この最小ハローからもっと大きなハローがどのように できるか、といった辺りを計算しようとしている。
さて、この講義も、当初予定していた
のうちの最初の3つまでが済んだということになる。もっとも、それぞれ大き なテーマであり、力学平衡モデルについては軸対称、あるいは3軸不等なモデ ル、あるいはディスク系とその不安定モードなどについては全く扱えていない。 (これは後半でなんとかしたい)力学平衡への緩和過程についても、例えば合体 の場合、あるいは理想化された1次元系を例にとって具体的な話をする必要も あったかもしれない。が、しかし、世の中は無衝突系だけではないし、また、 現実は無衝突系である場合でも、それを数値的にモデル化したものはそうでな くなってしまうことがある。従って、衝突系の進化がどのようなものかという ことは、実際になんらかの自己重力系を扱う場合には必ず理解しておく必要が ある。というわけで、これからしばらくで衝突系の進化というものを考えることに する。
まず、2体緩和とはいったいどういうものかというところから話を始め ることにする。原理的には、これがなにかというのは結構厄介な問題で ある。
有限粒子数の自己重力多体系を考えると、これは以下のような進化をす ると考えられる。まず、最初は力学平衡になかったとすると、とりあえ ず力学平衡に落ちつく。粒子数が無限大であれば、無限に細かく見れば 無限に時間がたっても真の力学平衡に到達するわけではないが、まあ、 漸近はしていく。この時、各粒子は与えられたポテンシャルの中を運動 するだけになり、それ以上進化することはなくなる。
さて、実際には有限粒子数であるので、そもそも真の力学平衡というも のはない。有限の質量をもった各粒子が系の中を運動するに従って、ポ テンシャルは必ず変化するからである。この変化によって各粒子の軌道 も変化することになる。
それでは、粒子の軌道の変化を、粒子数が有限であることから来る成分 とそれ以外に分離することは可能であろうか?これは、系が力学平衡に あるとみなすことができればそれは可能である。つまり、力学平衡にあれ ば、粒子のエネルギー変化は定義によりすべて粒子数が有限であること によるからである。
が、良く考えると問題なのは、そもそも有限粒子数であるものを力学平 衡とみなすとはどういうことかということである。このあたりを考えて いると段々混乱してくるので、まず、理想化された状況から考えていく ことにしよう。
理想化といえば例によって一様等方な分布を仮定することである。例え ばマックスウェル分布があって、その中の一つの粒子をとって考えると いうことをしたいわけだが、これは結構厄介なのでさらに簡単な例を考 える。すなわち、速度0で空間内に一様(ランダム)に分布した質点を考 え、その中を質量0のテスト粒子を飛ばして見る。
もちろん、この場合エネルギー交換はないので速度は変わらず、単に散
乱されるだけだが、しかし、この例は2体緩和のいくつかの重要な性質
を示すのですこし詳しく見ていくことにする。分布している質点の質量
を ![]() 、数密度を
、数密度を ![]() とする。テスト粒子が一つの粒子から距離(イン
パクトパラメータ)
とする。テスト粒子が一つの粒子から距離(イン
パクトパラメータ) ![]() を速度
を速度 ![]() で通った時に曲がる角度は、実際に
ケプラー問題の解析解を使って
で通った時に曲がる角度は、実際に
ケプラー問題の解析解を使って
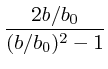 |
|||
| (2) |
さて、散乱の方向はランダムであると思われるので、平均としては(一
次の項は)0になる。しかし、 2次の項は0にならない。これは
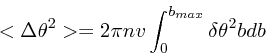 |
(3) |
この式から既にいろいろな性質がわかる。が、その前に理論的な困難を
解決しておく必要があるであろう。すなわち、この積分は
![]() で発散しているのである。これについてはいく
つかの考え方があった。例えば、初めて2体緩和の性質を理論的に調べ
た Chandrasekhar は、以下のように考えた。
で発散しているのである。これについてはいく
つかの考え方があった。例えば、初めて2体緩和の性質を理論的に調べ
た Chandrasekhar は、以下のように考えた。
「平均粒子間距離よりもインパクトパラメータが大きいような散乱は、 多体の干渉によって効かなくなるのでそこで積分を打ち切ってよい」
しかし、多体の干渉というようなものが実際にあるかどうかはあきらか ではない。もっと素直な解釈は、実際に系にあるすべての粒子と常に同 時に相互作用しているのだから、システムサイズくらいまで全部いれる (系が構造を持つ場合はちょっとややこしいが、密度の空間依存も積分 のなかに入れて全空間で積分する)というものである。
数値実験の結果などから、後者の解釈すなわち全体が効くというほうが 正しいということはかなり昔から大体わかっていた。歴史的には、どち らの解釈が正しいかについてはかなり最近まで論争があって、完全に決 着がついたといえるのは 94-5年頃である。が、これはまあそういうこと をいっている人もいたっていうくらいのもので、定説となっているのは 後者である。現在では後者の解釈が正しいということに疑いの余地はな い。
上の式から、適当に近似すると
| (4) |
さて、これからどんなことがわかるかというわけだが、これから、逆に
角度変化が1の程度になる時間というのを求めてみると、
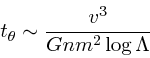 |
(5) |
今、![]() の質量依存性といったものを無視すると、散乱のタ
イムスケールは速度の3乗、数密度の逆数、質量の2乗の逆数に比例する
ということがわかったことになる。特に、質量密度一定の場合というも
のを考えてみると、タイムスケールが各粒子の質量に比例するというこ
とがわかる。
の質量依存性といったものを無視すると、散乱のタ
イムスケールは速度の3乗、数密度の逆数、質量の2乗の逆数に比例する
ということがわかったことになる。特に、質量密度一定の場合というも
のを考えてみると、タイムスケールが各粒子の質量に比例するというこ
とがわかる。
ある大きさを持った多体系というものを考えてみよう。質量![]() 、特徴的
な半径(ビリアル半径か何か)
、特徴的
な半径(ビリアル半径か何か) ![]() 、粒子数
、粒子数 ![]() とすれば、ビリアル定
理から
とすれば、ビリアル定
理から![]() 、力学的なタイムスケールが
、力学的なタイムスケールが
![]() となる。これを使うと上の緩和のタイムスケールは
となる。これを使うと上の緩和のタイムスケールは
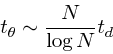 |
(6) |
2体緩和によって、最終的には系が熱力学的に進化するわけであるが、これが 普通の流体(ガス)とは本質的に違うものであるということをここで再確認し ておこう。
ガスの場合、粒子の平均自由行程はシステムサイズよりもはるかに小さい。液 体であれば平均粒子間距離は粒子のサイズ程度であるし、気体であっても通常 の状況では考えている現象の空間スケールに比べて平均自由行程は小さい。ち なみに、非常に希薄な気体とか、あるいは本当に空間スケールの小さい現象で は平均自由行程が問題になる。これは例えば超高層での人工衛星の回りの気体 の流れとか、あるいは最近の磁気ヘッドの回りの空気の流れとかいったもので ある。
とにかく、通常のガスの場合、平均自由行程がシステムサイズより小さく、シ ステムサイズよりは小さく平均自由行程よりは大きいような空間スケールを考 えると、そのなかでほぼ熱平衡になっていると思っていいことになる。いいか えれば、いわゆる Local thermal equilibrium (LTE) の仮定が使える。こう なると、温度とか圧力とかいった量が近似的(といっても実際上非常に高い近 似精度で)に定義でき、そういったマクロな量で系の進化を扱う、特に熱の流 れを拡散方程式で書くということが可能になる。
しかし、自己重力質点系では状況が全くことなる。まず、粒子数が無限大の極 限では、平均自由行程も無限大であった。つまり、 LTE がなりたたないどこ ろか、そもそも熱平衡に向かう(すなわちエントロピーを生成する)ようなメ カニズムがなかったわけである。
粒子数が有限の場合も、依然として平均自由行程が長い、つまり、粒子数無限
大の時の軌道から、他の粒子との相互作用によって段々ずれていくわけだが、
そのずれる典型的なタイムスケールは ![]() 程度であった。
つまり、流体の場合とは全く逆に、ほとんど自由運動(というか、他の粒子全
体が作るポテンシャルに沿った運動)をしていて、その場が有限の粒子で表現
されるための揺らぎがあるので段々軌道が変わっていくということになるわけ
である。
程度であった。
つまり、流体の場合とは全く逆に、ほとんど自由運動(というか、他の粒子全
体が作るポテンシャルに沿った運動)をしていて、その場が有限の粒子で表現
されるための揺らぎがあるので段々軌道が変わっていくということになるわけ
である。
従って、ローカルな熱平衡を仮定して拡散係数/輸送係数を求めるというのと は逆に、ある一つの粒子が系の中を動き回りながらどういうふうにエネルギー 等を変化させていくかという観点で見ていくことになる。
これをすこし別ないい方をすれば、通常の空間のなかでの密度や温度の変化を 考える代わりに、また6次元位相空間のなかでの分布関数の進化を考えるとい うことに当たる。具体的には、これまで無視してきた「衝突項」というものを ちゃんと評価して、どういうものかみてやろうということである。
さて、以下ではバックグラウンドの粒子分布のもとでの一つのテスト粒子の振 舞いを考える。前と違うのは、バックグラウンドも動いていることと、テス ト粒子も有限の質量を持つことである。バックグラウンドの粒子は一様に分布 するものとし、ある速度分布に従うとする。さらに、バックグラウンドの粒子 間の相互作用とかは考えないことにする。これで本当にいいかどうかはちょっ と良くわからない問題であるが、まあ、とりあえずやってみることにしよう。
前と同じく、分布している質点の質量
を ![]() 、数密度を
、数密度を ![]() とする。テスト粒子が一つの粒子から距離(イン
パクトパラメータ)
とする。テスト粒子が一つの粒子から距離(イン
パクトパラメータ) ![]() を相対速度
を相対速度
![]() で通った時に曲がる角度は、実際に
ケプラー問題の解析解を使って
で通った時に曲がる角度は、実際に
ケプラー問題の解析解を使って
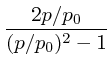 |
|||
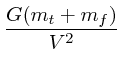 |
(7) |
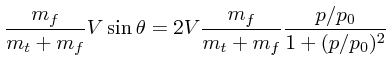 |
(8) | ||
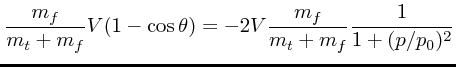 |
(9) |
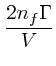 |
(10) | ||
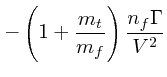 |
(11) | ||
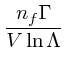 |
(12) |
| (13) |
上の式で、
![]() の項は前にでてきた角度の曲がる項と同じも
のである。前の話と違うのは、ネットに速度が小さくなる成分がある、すな
わち
の項は前にでてきた角度の曲がる項と同じも
のである。前の話と違うのは、ネットに速度が小さくなる成分がある、すな
わち
![]() が負で有限の値をもつということである。
が負で有限の値をもつということである。
これは、実は前にやった dynamical friction そのものであ
る。つまり、回りが止まっているなかを粒子が走っていくと、それが回りを引っ
張って動かすので、その分エネルギーを失って段々速度が落ちるわけである。
これは、 ![]() が大きい(
が大きい(![]() が小さい)極限では
が小さい)極限では ![]() 、つまり質量
密度によっていて、バックグラウンドの粒子の質量に依存しないことに注意し
てほしい。これに対し、他の項は
、つまり質量
密度によっていて、バックグラウンドの粒子の質量に依存しないことに注意し
てほしい。これに対し、他の項は![]() に比例していて、質量密度が同
じでも粒子の質量が大きいほうが値が大きくなるのは先週にやった通りである。
に比例していて、質量密度が同
じでも粒子の質量が大きいほうが値が大きくなるのは先週にやった通りである。
さて、ここではとりあえず1次と2次の項を求めたわけだが、それより先の項に ついては考えなくてもいいのだろうか?ここでは粒子の軌道変化がたくさんの 散乱のランダムな重ね合わせで書けるとした。この仮定が正しければ、たくさ ん散乱を受けた後の速度の分布は1次と2次のモーメントで決まるガウス分布に なり、従って3次より高いモーメントの寄与は考えなくてもいいことになる。
問題はこの仮定が正しいかどうかであるが、実は理論的にはそれほど正確なわ
けではない。というのは、インパクトパラメータが例えば ![]() の程度の散
乱というのも現実におき、その効果はそれ以外の散乱すべての寄与に比べてせ
いぜい
の程度の散
乱というのも現実におき、その効果はそれ以外の散乱すべての寄与に比べてせ
いぜい ![]() 程度でしか小さくないからである。まあ、しかし、そ
んなことをいっていても高次の項があっては計算出来ないし、とりあえず
程度でしか小さくないからである。まあ、しかし、そ
んなことをいっていても高次の項があっては計算出来ないし、とりあえず
![]() 程度で小さいということも確かなので、以下高次のモーメン
トは考えない。
程度で小さいということも確かなので、以下高次のモーメン
トは考えない。
この文書はLaTeX2HTML 翻訳プログラム Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds,
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
を日本語化したもの( 2002-2-1 (1.71) JA patch-1.9 版)
Copyright © 1998, 1999, Kenshi Muto, Debian Project.
Copyright © 2000, Jun Nishii, Project Vine.
Copyright © 2001, 2002, Shige TAKENO, Niigata Inst.Tech.
Copyright © 2002, KOBAYASHI R. Taizo, Project Vine.
を用いて生成されました。
コマンド行は以下の通りでした。:
latex2html -nomath_parsing -local_icons -show_section_numbers -split 0 note6-e.tex.
翻訳は Jun Makino によって 平成24年9月30日 に実行されました。