
さて、ここまで数値積分の話をしたわけだが、微分方程式の数値解法と数値積 分はもちろん非常に良く似たものである。が、大きな違いは、数値積分では被 積分関数が

と、独立変数の陽な関数として与えられていたのに対し、微分方程式では

と積分された結果自体に被積分関数がよっていることである。このために、話 がすこし複雑になる。
例えば、もっとも簡単な中点公式の場合を考えてみよう。数値積分の場合には、 単に

であった。微分方程式の場合、問題は 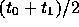 での x の値を我々
はまだ知らないということである。
での x の値を我々
はまだ知らないということである。
この困難は、数値積分が近似多項式の積分として与えられたということを思い
出せば一応解決できる。中点公式の場合、数値積分ではこれはfを
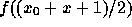 で近似するということに相当した。同様なアイディアを微分
方程式に適用すれば、微分方程式の場合、 fを定数で近似し、その結果解で
ある x を一次式で近似する、つまり
で近似するということに相当した。同様なアイディアを微分
方程式に適用すれば、微分方程式の場合、 fを定数で近似し、その結果解で
ある x を一次式で近似する、つまり
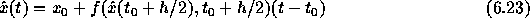
という近似をする。これから、問題の中点での値を 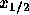 と書くと
と書くと
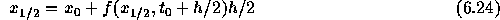
と書けるわけで、これは 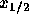 に対する代数方程式になっている。これを
解けば数値解も求まるわけである。
に対する代数方程式になっている。これを
解けば数値解も求まるわけである。
一般には、n次のルジャンドル多項式から導かれる公式では、fの n-1次
近似多項式を構成することになる。これを前節と同様 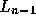 とし、零点を
とし、零点を
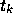 とすれば、
とすれば、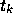 での「解」
での「解」 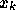 が
が
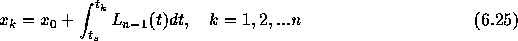
がなり立ち、さらに

がなり立つように 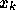 と L を決め、それを積分して
と L を決め、それを積分して 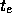 での解が求
まるということになる。
での解が求
まるということになる。
と書くと非常に大変そうだが、係数をあらかじめ計算しておけば上の手続きが 陰的ルンゲクッタ公式として表現できる。これで、例えば 4 段で 8 次の公式 が実現出来るわけである。