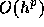 で押えられるとい
うことになる。従って、数値解がどの程度正しいかということに関しては非常
に正確に押えられる。
で押えられるとい
うことになる。従って、数値解がどの程度正しいかということに関しては非常
に正確に押えられる。
非線形問題の場合の数値解の振舞いの解析は、線形問題の場合に比べてはるか に困難になる。この根本的な理由は、前にやった安定性の場合と同様、数値解 が真の解に近いかどうかということが、真の解が「可積分」でないとうまく定 義できないからである。
ここで、可積分というのは、もとのハミルトン力学系の性質として解析的な解 を持つということである。これがじゃあいったいどういうことかというのは、 やりはじめるとそれだけで1学期かかるので、興味がある人は「力学」(大貫良 夫、吉田春夫、岩波書店)でも見てもらうことにする。
とはいえ、定義を与えないと話が進まない。ある力学系が可積分であるという のは自由度の数と等しい数の保存量を持つことである。この時は、位相空間内 での軌道が(多重)周期軌道になる。いいかえれば、カオス的にはならない。 逆に、可積分でないということとカオス的であるということはほぼ対応する。 (もちろん微妙な場合というのがあるが)
さて、非線形の場合でも、厳密解が周期解ならばシンプレクティック公式や対
称型公式で求めた数値解も周期解になるということが非常に最近になって証明
された。ここではこの証明がどういうものかは触れないが、この場合には厳密
解と数値解の間の差が線形の場合とおなじように 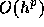 で押えられるとい
うことになる。従って、数値解がどの程度正しいかということに関しては非常
に正確に押えられる。
で押えられるとい
うことになる。従って、数値解がどの程度正しいかということに関しては非常
に正確に押えられる。
さて、なぜわざわざ数値計算をするかということを考えてみると、多くの場合 には可積分ではないから数値計算するのである。可積分ならば数値計算しなく ても解が求まるはずだからである。
しかし、この場合には、数値解の正しさというものの意味はあまり自明ではな くなる。というのは、もともとの厳密解の場合にも「正しい解」というものの 意味が明確ではなくなるからである。
可積分でないということとカオス的ということはほぼ対応すると考えて良いの で、以下カオス的である場合について考える。カオス的であるための必要条件 は、リヤプノフ指数が正であることであった。
リヤプノフ指数が正であるというのはどういうことかというと、非常に近い初 期条件から出発した厳密解の間の距離が、指数関数的に広がるということであ る。従って、仮に数値解が本当に厳密解通りのものを求めていたとしても、初 期条件に誤差があればそれが指数関数的に拡大し、しばらくすれば真の解から 大きくずれてしまうといったことが起きる。
この場合、数値計算をする目的により、どのような解に意味があるか、また、 どのような計算が可能かということが違ってくる。
まず、何が不可能かということを明確にしておこう。初期条件が有限の精度で しか知られていなければ、その誤差が指数関数的に増大するため、仮に無限に 高い精度で数値計算したとしても、ある時刻での解の精度には限度があり、そ の限度が時間の指数関数で悪くなっていく。従って、誤差の指数関数的な成長 のタイムスケールの例えば 10 倍とか 30倍を越えて正確な軌道を求めるとい うことは原理的に不可能である。
従って、可能なことは以下の2つということになる。
第一の場合にはなにを計算しているかは明確であり、誤差も精密に評価出来る。 つまり、リヤプノフ指数が前にやったリプシッツ連続の条件の値そのものなの で、誤差の上界が大域誤差の式でほぼ正確に押えられるのである。この場合に はそれほど議論するべきことはない。
それでは、第二の場合についてはどうであろうか?
こちらは、実は理論的にも実験的にもまだ良くわかっていないのが現状である。
シンプレクティック法の場合には、それで求まった解が元のハミルトニアン
H に近い 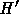 で表される系の厳密解になっていることがあるという話をし
たが、そのようなものが具体的に求まっているのは実は可積分な系に限られて
いて、非可積分なハミルトン力学系に対してシンプレクティック法を使った時
に良いことがある、つまり
で表される系の厳密解になっていることがあるという話をし
たが、そのようなものが具体的に求まっているのは実は可積分な系に限られて
いて、非可積分なハミルトン力学系に対してシンプレクティック法を使った時
に良いことがある、つまり 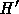 が存在するかどうかはわかっていない。つま
り、形式的に級数で書けるものの、それが収束するかどうかは知られていない。
が存在するかどうかはわかっていない。つま
り、形式的に級数で書けるものの、それが収束するかどうかは知られていない。
しかし、それにも関わらず、実験的には多くの場合に良い結果が得られている。 では、ここで、良いというのはどういう意味かというと、単に保存量であると わかっているもの、例えばエネルギーや、系によっては角運動量といったもの の誤差が成長していかない、つまり有界に留まるということである。
このことがもっとも良く知られているのは分子動力学計算である。分子動力学 計算というのは、例えば水とかタンパク質とかいったマクロな物質の物性や非 平衡な変化を、ミクロな分子一つ一つの軌道を時間積分して計算することで調 べようというものである。もちろん、実際の水を構成している分子の数はあま りの多いので、そのまま計算することはできず、せいぜい 1000個とか 10,000 個程度の分子から出来た系について計算していろいろ調べるということになる。
この時、分子一つの軌道については、それが隣の分子までのの距離を動くくら
いの時間が上のリヤプノフ指数に入ってくることがわかっている。これは具体
的には 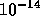 秒程度である。これに対して、数値計算で熱平衡状態の分
布関数を求めるといった場合には
秒程度である。これに対して、数値計算で熱平衡状態の分
布関数を求めるといった場合には 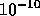 乗程度、非平衡の変化の場合も
同程度の計算が必要になる。
乗程度、非平衡の変化の場合も
同程度の計算が必要になる。
従って、計算は指数関数のタイムスケールの 1万倍程度することになり、誤差 は「分子がどこにあるかは全くわからない」という程度には大きい。つまり、 例えばある分子の位置を初期条件で最後の1ビットだけ変えただけで、計算が 終った時のその粒子の位置は全く変わってしまう。
この場合に計算結果に意味があるといえるかどうかは実はまだ理論的にははっ きりしていない。分子動力学計算の一つの目的は、熱平衡状態での系の性質 (温度と圧力の関係とか、拡散係数など)を決めることであり、この場合には 数値解が厳密解である必要はなく、それがエルゴード性を満たしていればいい。 ところが、このエルゴード性というのが、そもそも元のハミルトン系が満たし ているかどうかがまだ一般にはわかっていないという代物である。数値解が同 なっているかなんてことは従っていっそうわからないのである。
そういう意味では、分子動力学計算に代表されるような、系の統計力学的な性 質を直接シミュレーションによって調べるという方法の理論的な正当性は明ら かではない。この根本的原因は、しかし、統計力学自体の理論的な正当性が明 らかではないところにある。
つまり、カオスになっているような系の長時間計算では、理論的には意味があ る答が出ているという保証はない。実験的にはうまくいく、つまり統計的な性 質が理論的に予測できるものについては良く一致するということがわかってい て、広く使われているのであるが。