以下はN君との議論に触発されて思い付いただけの話でちゃんとした定量的な検討
はできてないです。
ポアソン方程式の周期境界条件での解を求める普通の方法はもちろん FFT で
あり、粒子系についてはエバルド法、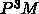
、PME といったものが使われる。
これらの方法は(単純なエバルドを除いて)計算量が基本的に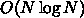 
の程度で少ない、というのが特色だが、FFT であるために大域的で量が多い
通信が発生する、というのが問題点である。
さて、周期境界を扱う方法はもちろんFFTだけではない。数学的には、実際に
無限和をとる、という方法もありえる。形式的には、単純に一つの粒子の
ミラーイメージを無限に沢山考えると、和をとる順番で答が変わりえるので
ややこしいが、箱の平均密度が0になるように負の質量を分布させておけば
この問題は避けられる。
負の質量を分布させる上での問題点は、相互作用を直接計算している近傍の処理
である。原理的には、反質量粒子を格子上に本当において、それらからの
力は大きいめのソフトニングをいれて評価し、さらに一様な分布から残る残差
は適当な近似多項式等で補正すればよい。1粒子当りの計算量は若干増えるが、
近傍の粒子を直接計算する計算量は必ずあるのでそれに比べるとたいしたこと
はない。あるいは、ちゃんと立方体のポテンシャルの球面関数展開を使うので
もよい。
この方法のメリットは通信量にある。例えば4096 プロセッサ (16^3グリッド)
で領域分割し、2048^3 程度の粒子数を使う場合を考えてみる。FFT を 1024^3
でやると、バイセクションで全部のデータが移動するので10GB 程度の移動、
3D メッシュネットワークだとするとチャネル当たり40MB 程度のデータ移動
が必要になる。
一方、多重極展開では通信量は基本的にツリーの場合と同じで、下のほうの、
距離が近い通信が大きい。単純な実装では、 all-to-all 放送で
少なくとも全体の展開1つは渡す必要があり、これを4重極くらいですますとす
ると9語、全部で300kB 程度をなにかする必要があるが、FFTの場合とは桁違い
である。もちろん、FFT でも256^3 まで減らすと通信は減るはずだが、
そこまで減らすとツリーの部分の精度をかなり上げる必要がでてくる。
なお、 TreePM でも同様に負の質量を分布させることで現在の方法での誤差の
主要項をなくすこともできる。そうすると、例えば宇宙論的計算では初期の一
様密度に近い時の計算量、通信量をかなり減らすことができるであろう。
Anton では 512 プロセッサで数万原子、FFT は32^3 で 32k語, チャネル毎に
500語 が流れる。512プロセッサの展開を all-to-allでやると同程度の通信が
発生して面白くないが、放送するのはさらに1レベル上の展開にすれば 1/8 に
できるのでそれなりにメリットはあると考えられる。