2ちゃんねるで解説を要求されたから書くわけではありません。
3次元の議論をするのが本当ですが、面倒なのでまず1次元で考えます。
偏微分方法の差分化は(境界条件とか細かいことをはぶくと)
unew[i] = f(uold[i-1], uold[i], uold[i+1]);
というような感じに書くことができます。ここで u は格子点 i での物理量で、
なので流体方程式ならスカラーではなく速度、圧力、密度くらいの3変数です。
なお、上のは3点差分の場合で、空間微分の次数を上げるなら u[i-2], u[i+2]
といったものもはいってきますが、原理は同じです。これをシリアルに処理す
る時には以下のような感じでするのが普通です。
uim1 = u[0];
for(i=1; i<n-1;i++){
uold = u[i];
u[i] = f(uim1, uold, u[i+1]);
uim1 = uold;
}
要するに、自分の更新のためには両側の古い値が必要ですが、左側を更新して
しまっているので更新前の値を一時的に残しておく必要があるわけです。但し、
これはあくまでも一時的なので、全部の変数を2重にもつとかいった必要はな
く、必要なメモリ量は格子数×3語で十分です(もちろん、一時変数の分や、
関数 f の計算に必要な分がありますが、これらは格子数に依存しません。
さて、ではメモリアクセスはどうか、という話です。理想的に良くできたキャッ
シュとかがあれば、 u は u[i+1] のアクセスの時にキャッシュにはいって、
u[i]= の代入がメモリに反映される時に書き込みが起こるだけです。 f の評
価で巨大なテーブルを読むとかがなければ、ここでも主記憶へのアクセスは不
要です。従って、原理的には主記憶へのアクセスは1ステップ当り
3N語(Nは格子数)読んで書くだけしか必要ありません。
この事情は2次元でも3次元でも同じで、陽解法である限り原理的には主記憶ア
クセスは1ステップ当り1度読んで書くだけにできます。流体計算の格子点当り
の演算数は結構多く、例えば3次元 Roe 法では 1000演算程度です。そうすると
5語の読み書きで 1000演算ですから、いわゆる B/F (Byte-per-Flops) 値でい
うと 0.08 ということになります。流体計算ではB/F=4 が必要とかいう話があ
りますが全然そんなことはなくてその 1/50 でいいわけです。
現実のキャッシュは理想的ではないとか色々問題はあるのですが、
それは計算機の作り方が阿呆なだけであって、阿呆な作り方のために
もっとも貴重なリソースである外部メモリバンド幅をドブに捨てている
にすぎない、ということです。
なお、メモリバンド幅をさらに減らすことはできないか、ということも
考えることができます。これにはどうすればよいかというと、例えばさらに半
分にするには1度メモリから読んで1ステップでなく2ステップ進めればよいこ
とになります。1次元計算の場合には、例えば
u[i] = f(u1im, u1i, u1ip)
u1im = u1i
u1i = u1ip
u1ip = f(u[i+1],u[i+2],u[i+3])
(ちゃんと考えてないので間違っているかもしれません)というようなものを
実行すればよいし、コードが煩雑になりますが3ステップ以上進めることも
可能です。なお、1次元の場合はこのように、nステップ進めるためには
nくらいの数の一時変数があればすみますが、 3 次元の場合には
単純には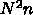
くらい、これより少ないと若干メモリアクセスが増える
ことになります。