5. 楕円型方程式
楕円型方程式は、典型的にはラプラス方程式
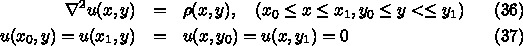
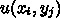 は重力定数、
は重力定数、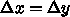 は物質の質量密度(単位体積あたりの質量)である。
ここで、
は物質の質量密度(単位体積あたりの質量)である。
ここで、 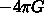 はとりあえず与えられた空間座標だけの関数とする。空間1次元ではラプラシアンがただの2階微分演算子になって
しまい、解くべき方程式は常微分方程式ということになる。
はとりあえず与えられた空間座標だけの関数とする。空間1次元ではラプラシアンがただの2階微分演算子になって
しまい、解くべき方程式は常微分方程式ということになる。
実際にポアソン方程式(とさらに状態方程式を連立させてでてくるレーン・エ ムデン方程式)を球対称の場合に解くというのは I のほうでやったと思うの で、ここでは空間2次元の場合を考える。3次元も考え方は同様である。
工学的な応用では、楕円型方程式の応用として重要なのはラプラス方程式の境 界値問題である。これは、構造解析、電場の解析などあらゆるところで現れる。 特に複雑な形状の機械部品とか機械全体の中での応力場の解析といったものが 重要な応用ということになる。
が、天文・物理のいろんな問題では、複雑な境界値問題というのはあんまり大事では ない。天体は大抵重力でまとまっているわけで、固定された表面(境界)とい うものが与えられているとは限らないからである。もちろん、数値計算の方法 によってはそういうものが出てくることもあるが、とりあえず今日は比較的に 単純な境界条件だけをかんがえることにしよう。
ラプラス方程式やポアソン方程式は、基本的には拡散方程式から時間微分の項 を落したものと考えることができる。つまり、なんらかの定常状態を記述して いるわけである。多くの応用で、実際にそのような定常状態を求めているわけ であるが、数値計算という観点からすると、ラプラス方程式やポアソン方程式 に適用できる計算法は実は拡散方程式や波動方程式に陰解法を適用する時にも 使える。
これは、前回見たように陰解法では空間方向の差分方程式を解く必要がでてく るからである。解くべき方程式は、ラプラス方程式やポアソン方程式の差分化 からでてくるものと基本的には同じである。
というわけで、今日は、単純な2次元ポアソン方程式の境界値問題を例に、計 算方法について考えていく。
2次元なので、ラプラシアンは
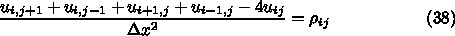
 と書き、これが
と書き、これが  の近
似解としよう。また、前回と同じ2次精度の中心差分を使うとすれば、ラプラ
シアンの差分近似は以下で与えられる。
の近
似解としよう。また、前回と同じ2次精度の中心差分を使うとすれば、ラプラ
シアンの差分近似は以下で与えられる。

 とした。いま、解くべき問題を長方
形領域でのポアソン方程式の境界値問題
とした。いま、解くべき問題を長方
形領域でのポアソン方程式の境界値問題

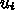 の項は 1 とする)、
これは2次元配列 u[nx][ny] についての線形連立方程式ということになる。
ここで
の項は 1 とする)、
これは2次元配列 u[nx][ny] についての線形連立方程式ということになる。
ここで

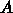 , それ
以外では
, それ
以外では
さて、というわけで、2次元の長方形領域上でのポアソン方程式の差分近似は、
連立線形1次方程式 ( 41 )になるので、これを何らかの方法
で解けばいい。
空間1次元の場合には、出てくる行列が3重対角という特別な性質を持ったもの
であったので、自由度(要素数)に比例する計算量やメモリー使用量で方程式
を解くことができた。
2次元の場合はどうなるかというと、そんなにうまくはいかないということが
わかる。もちろん、2次元の場合でも、
このために、計算量としては
もちろん、これでも一般の場合のガウスの消去法の計算量である
このために、ガウスの消去法のようにまともに行列を解くのではなく、適当な
近似を繰り返していくことで解を求めることはできないかということが昔から
考えられてきた。以下、その方法のいくつかを紹介する。これらを反復法とい
う。
なんらかの方法で適当な近似解
一つの方法は、行列 A を形式的に以下のように分解することである。
この反復で、収束すれば、つまり、
実用上は、収束したかどうか判定する必要がある。これには、普通は
理論的には、数列は連続する2項間の差が小さくなっても収束に近付いている
とは限らないが、ガウス反復の場合には、丸め誤差がなければこれで判定でき
ることが証明できる。
が、この方法には2つ問題がある。一つは収束が非常に遅いことであり、もう
一つは u と unew で配列が2ついるのでメモリがたくさん必要に
なることである。
さて、実は、上の2つの問題は一度に解決することができる。上のプログラム
を、以下のように変えてしまうのである。
形式的には、これは以下のように書くことができる。 行列
収束の速さをガウス反復について検討する。面倒なので1次元として、
なお、式 48 は、前節で扱った拡散方程式の陽解法差分近似とみな
すこともできることに注意して欲しい。なので、上のように天下りに固有関数
を仮定しなくても、前節と同様に線型差分方程式であることから解を求めるこ
ともできる。線形差分であることから指数関数型に限られるため、周期解は
フーリエ級数解なので、2つの方法は数学的には等価である。
また、陽解法の安定性条件を満たすように、
ガウス・ザイデル法についても同様に必要な反復回数を求めることができる。
次に述べる SOR についても(多分)できる。
というわけで、ガウス・ザイデルはガウス反復よりはましだが、まだもうちょっ
となんとかならないものかという気もする。実際に近似解の挙動を見るとわか
るが、どちらの方法でも、誤差の減り方にはパターンがあって、1方向から真
の解に近付いている。
というわけで、以下のようなことが考えられる:ガウス・ザイデル法で、修正
量
こんな安直な方法で大丈夫なのかと思うであろうが、うまくいってしまうのが
すばらしいところである。プログラムとしては、ガウス・ザイデルの時の式を
ちょっと変えて、
この方法を SOR (Successive Over Relaxation, 本によっては Simultaneous ...
となっているものもあるかもしれない)という。
天文等で出てくるポアソン方程式の場合には、特にうまく
ADI は alternating direction implicit の略である。ここでの基本的な考察
は、「3重対角なら簡単に解ける」ということである。これを使って、
もうちょっとちゃんと書いてみると、例えば
ただし、実際に使う上では、 SOR と同じように、修正量の補正をしたほうが
収束が速い。 SOR とは逆に修正量をすこし減らす必要があり、どれくらい減
らすべきかを決めるのにはまたややこしい理屈がいる。
ただし、適当に修正量を決めても最適な SOR よりも遅くはない程度で収束す
るという利点がある。
共役勾配法は、実は、現在大規模な行列を解くのにはもっとも広く使われてい
る方法である。これは、特にいろいろな前処理と組み合わせることで、例えば
拡散方程式の定常問題で拡散係数が空間に強く依存する場合にも収束させられ
るとか、刻みを場所によって変えるような高度な方法でも同様になんとかでき
るとかいう利点があるからである。
しかし、これは安直にプログラムを書いただけではこれまでの紹介してきた方
法に比べて速くなくて、いろいろ高度な変形をして初めて速くなる。また、ほ
とんど共役勾配法だけについて議論した良い教科書がいくつもあるので、ここ
では省略する。ここでは、とりあえずそういう名前のものがあるということく
らいをちょっと憶えておいてほしい。
とはいえ、極めて重要な方法ではあるので、これについては、もうちょっと数
学的な準備をした後でもう一度やることにする。
ポアソン方程式を解く方法の一つで、応用上は重要なのはフーリエ変換を使っ
た方法である。いま、固定境界をやめて周期境界条件でいいことにすると、ポ
アソン方程式の場合、
これは極めて強力かつ高速な方法であり、
星の構造を解くとかいう場合だと、極座標を使って球面調和関数展開というこ
とも多い。この場合の計算には FFT のようなうまい方法があるわけではない
(最近高速ルジャンドル変換の研究もあるが、これはよほど項数が大きくない
と速くならない)が、
ガウス・ザイデル法で上のポアソン方程式の境界値問題を解くプログラムを作成せよ。
ただし、
さらに、 SOR について同様に調べよ。最適な
上と同じデルタ関数の時に数値解を求めて、 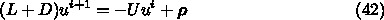
5.1. 線形方程式と反復法
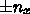 という
ように添字をふりなおして(以下、添字が1つしかないときにはこのように付け変えたものを考える
ということにする)、以下のように行列の形に書くことはできる。
という
ように添字をふりなおして(以下、添字が1つしかないときにはこのように付け変えたものを考える
ということにする)、以下のように行列の形に書くことはできる。

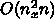 は
は 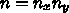 のベクトル表示である。
しかし、
のベクトル表示である。
しかし、 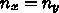 の要素を考えてみると、対角要素、その両側の他に、
の要素を考えてみると、対角要素、その両側の他に、
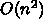 だけ離れたところに 0 でない要素が現れる。
だけ離れたところに 0 でない要素が現れる。
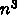 (
(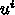 として)になり、1次
元のときよりずっと計算量が多い。例えば
として)になり、1次
元のときよりずっと計算量が多い。例えば 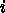 、つまり正方形領域と
すれば計算量は結局
、つまり正方形領域と
すれば計算量は結局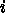 になってしまう。
になってしまう。
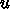 より
は少ないが、しかし非常に多いことには変わりはない。また、3次元の場合に
はこの状況はいっそう悪化する。
より
は少ないが、しかし非常に多いことには変わりはない。また、3次元の場合に
はこの状況はいっそう悪化する。
5.1.1. ガウス反復
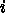 (ここで上つき添字
(ここで上つき添字  は
は 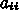 番
目の近似解ということで、別に
番
目の近似解ということで、別に  の
の  乗という意味ではない。下につけ
ると他の添字と混乱するので上につけてみた)があるとする。これをもうちょっ
とましな解にできないかということを考える。
乗という意味ではない。下につけ
ると他の添字と混乱するので上につけてみた)があるとする。これをもうちょっ
とましな解にできないかということを考える。
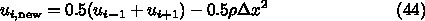
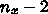 は対角要素
は対角要素 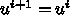 だけをとりだした行列で、
だけをとりだした行列で、 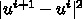 はそれ以
外の残りである。これを使って、以下のような式を考える
はそれ以
外の残りである。これを使って、以下のような式を考える
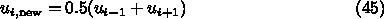
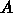 は対角行列なので、これは解けていて、実際のプログラムとしては、
は対角行列なので、これは解けていて、実際のプログラムとしては、
for (i=1; i<nx-1;i++){
for (j=1; j<ny-1;j++){
unew[i][j] = 0.25*(u[i][j-1]+u[i][j+1]+u[i-1][j]+u[i+1][j])
- rho[i][j]*0.25*deltax*deltax;
}
}
ということになる。1で始まって  等で終っているのは、境界は 0 固
定だからである。その分の配列を節約することも考えられるが、いじましいし
ちょっとわかりにくくなるので上の形に書くことにしよう。
等で終っているのは、境界は 0 固
定だからである。その分の配列を節約することも考えられるが、いじましいし
ちょっとわかりにくくなるので上の形に書くことにしよう。
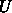 となれば、これら
が元の方程式を満たしていることは明らかであろう。収束するかどうかは面倒
なのでここでは省くが、上のような簡単なポアソン方程式の離散化で妙な非線
形項とかがなければ収束するということが証明できる。
となれば、これら
が元の方程式を満たしていることは明らかであろう。収束するかどうかは面倒
なのでここでは省くが、上のような簡単なポアソン方程式の離散化で妙な非線
形項とかがなければ収束するということが証明できる。
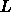 を計算してそれが適当な設定した値よりも小さく
なったらいいことにする。
を計算してそれが適当な設定した値よりも小さく
なったらいいことにする。
5.1.2. ガウス・ザイデル法
for (i=1; i<nx-1;i++){
for (j=1; j<ny-1;j++){
u[i][j] = 0.25*(u[i][j-1]+u[i][j+1]+u[i-1][j]+u[i+1][j])
- rho[i][j]*0.25*deltax*deltax;
}
}
なにをしたかというと、 unew というのをやめにして u にした
だけである。つまり、一回の反復の中では u の要素を順に変えていくわ
けだが、その時に、既に新しい値が求まっていればそっちを使おうというだけ
のことである。新しい値のほうが、多分より正確であろうと考えられるからで
ある。
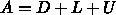 を、対角成分
を、対角成分
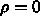 、非対角成分の上半三角分
、非対角成分の上半三角分 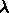 、残り
、残り 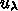 の3個に分ける (
の3個に分ける (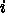 )と、
)と、
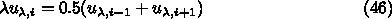
5.1.3. 収束の速さ

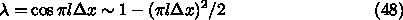
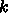 としてよくて、
としてよくて、

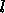 と固有ベクトル
と固有ベクトル 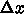 が
が


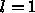 は虚数単位で
は虚数単位で 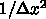 が格子のインデックスとす
る。
が格子のインデックスとす
る。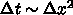 はフーリエモードのインデックスである。これを
49 にいれて整理すると
はフーリエモードのインデックスである。これを
49 にいれて整理すると
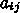
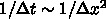 を与えると
を与えると 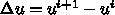 の時にもっ
とも1に近く、収束が遅いことがわかる。また、反復回数は
の時にもっ
とも1に近く、収束が遅いことがわかる。また、反復回数は
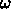 程度必要であることもわかる。
程度必要であることもわかる。
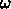 となっている。収束までは
時間が1より十分大きくなる必要があるので、反復回数が
となっている。収束までは
時間が1より十分大きくなる必要があるので、反復回数が
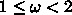 程度必要となる。
程度必要となる。
5.1.4. SOR
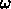 に適当な係数
に適当な係数 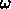 を掛けて水
増ししてやればもうちょっとうまくいくのではないか?
を掛けて水
増ししてやればもうちょっとうまくいくのではないか?
u[i][j] += omega*(0.25*(u[i][j-1]+u[i][j+1]+u[i-1][j]+u[i+1][j])
- rho[i][j]*0.25*deltax*deltax -u[i][j])
というだけで済む。実際的な問題は、  の値をどうとるかということ
である。理論的には
の値をどうとるかということ
である。理論的には 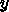 でないといけないことがわかっていて、
さらに本当はもちろん線形のポアソン方程式とかなら最適な
でないといけないことがわかっていて、
さらに本当はもちろん線形のポアソン方程式とかなら最適な 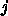 の値
が計算できるが、ここではそこまでは立ち入らないことにする。
の値
が計算できるが、ここではそこまでは立ち入らないことにする。
5.2. もっと高度な解法
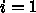 を決めら
れれば SOR で非常にうまくいくことが多い。が、まあ、世の中はそういう問
題ばかりでもないので、それ以外の方法を紹介だけしておく。
を決めら
れれば SOR で非常にうまくいくことが多い。が、まあ、世の中はそういう問
題ばかりでもないので、それ以外の方法を紹介だけしておく。
5.2.1. ADI
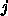 方
向と
方
向と 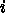 方向を交代で解いているうちになんとかなって欲しいというのが
ADI の考え方ということになる。
方向を交代で解いているうちになんとかなって欲しいというのが
ADI の考え方ということになる。
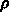 方向に解くときには、
方向に解くときには、
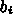
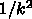 から順に解
いていく。
から順に解
いていく。 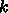 方向が終ったら次は
方向が終ったら次は 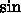 方向をやる。
方向をやる。
5.2.2. 共役勾配法
5.2.3. FFT を使った方法
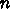 をフーリエ級数展開して、出てきた係数に
をフーリエ級数展開して、出てきた係数に
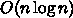 (
(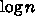 は波数)を掛けてから逆フーリエ変換すればポアソン方程式の解
になっているわけである。固定境界なら
は波数)を掛けてから逆フーリエ変換すればポアソン方程式の解
になっているわけである。固定境界なら  関数だけで展開すればよい。
フーリエ変換の計算量は多次元でも格子点の総数を
関数だけで展開すればよい。
フーリエ変換の計算量は多次元でも格子点の総数を 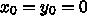 として
として 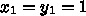 の程度なので、これは反復法でいうと回数がせいぜい
の程度なので、これは反復法でいうと回数がせいぜい 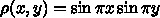 で済むという
ことに相当する。
で済むという
ことに相当する。
という条件がすべて満足されていれば、必ずこの方法を使うべきといってもさ
しつかえない。
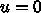 方向は展開しないで済ませられるのでまあつかえな
くはない。
方向は展開しないで済ませられるのでまあつかえな
くはない。
5.3. 練習
5.3.1. 練習1
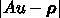 ,
, 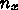 としてよい(入力パラメータとして読め
る汎用的なプログラムを作ってくれればもちろんそのほうがよい)。
さらに、
としてよい(入力パラメータとして読め
る汎用的なプログラムを作ってくれればもちろんそのほうがよい)。
さらに、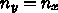 として、初期推定
として、初期推定 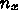 から出発した時に
から出発した時に
を空間刻み 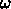 が反復を繰り返した時にどのように 0に近付くか
が反復を繰り返した時にどのように 0に近付くか
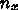 (
(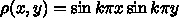 としてよい) のいくつかの値について調べ、そ
れから精度が
としてよい) のいくつかの値について調べ、そ
れから精度が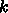 の何乗になっているか議論せよ。
の何乗になっているか議論せよ。
5.3.2. 練習2
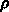 の値は
の値は
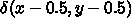 に依存するかどうかも議論すること。
に依存するかどうかも議論すること。
5.3.3. 練習3
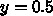 (
( は整数)の時に、誤差は
どうなるか、理論的または数値的(両方あればそれもOK)議論せよ。
は整数)の時に、誤差は
どうなるか、理論的または数値的(両方あればそれもOK)議論せよ。
5.3.4. 練習4
 がデルタ関数
がデルタ関数  の時に、厳密解をフーリエ級数の形で表せ。
の時に、厳密解をフーリエ級数の形で表せ。
5.3.5. 練習5
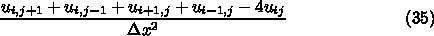 の線上で誤差が
どのように分布するか調べよ。また、誤差の等高線表示や3次元表示を適当な
ツールを使って作ってみよ。
の線上で誤差が
どのように分布するか調べよ。また、誤差の等高線表示や3次元表示を適当な
ツールを使って作ってみよ。