6. 常微分方程式
ルンゲクッタ法とは、非常に一般的には以下のような形に書ける方法である。
と、こう、式に書いてしまうとすぐにはわからないが、例えば
のことをさす。これは、いろいろ良い性質をもつ。例えば
4次よりも高精度な公式というのも非常によく研究されていて無数にいろんな
ものが知られている。ただし、4次よりも高い次数では、次数よりも必要な段
数が大きくなる。この2つの関係が一般にどうなるかは未解決の問題である。
というようなこともあるので、よほど変わったことをしたいというのでない限り、専門
家が作った公式を使うのが無難である。
Dormand と Prince は、段数/次数のさまざまな組合せについて、
離散化誤差を非常に小さくした公式を求めている。これらは、
普通の(というのがどういう意味かは今のところ明らかではないが)常微分方
程式を手軽に解くにはこれらのRK公式を使えば十分である。
実用的には、こちらが欲しい計算精度をどうやって達成するかという問題があ
る。この問題を解決するためには、誤差を推定しながら積分の刻み幅を自動的
に調節する必要がある。これについては次回にちょっと触れる。
さて、「普通は」RKで十分というのは、もちろん時と場合によっては違う方法
を使うべきであるという意味である。なぜそういう場合があるかというのは、
以下の理由による。
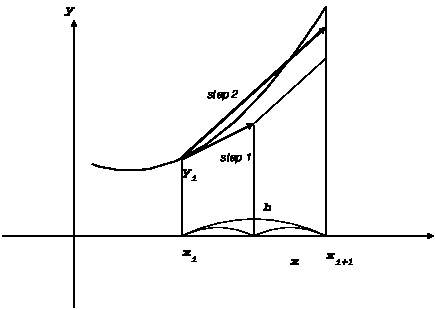
RK 法は、「一段階」法である。これはどういう意味かというと、微分方程式
これに対して、一段階ではない方法、つまり多段階法というのは、
さらに、「一段階でない」というだけなので、可能な計算法にあまりに多様な
可能性がある。一例として、以下のような方法が考えられる。
この方法は、しかし、立派な名前までついているのにもかかわらず、実は使え
ない公式である。
どのような問題があるのかを示すために、以下の線形方程式
ちょっと式を見ればわかるように、絶対値が 1 より大きい固有値は
なお、上のような、安定な線形微分方程式について振舞いを調べるというのが、
常微分方程式の安定性解析の基本になる。非線形な方程式では違うとかいろん
なことがあるかもしれないわけだが、まあ、少なくとも線形安定でないと話に
ならないし、それ以上のことは一般論としていうのは難しいからである。
さて、安定でちゃんと使える線形多段階法はじゃあどんなものか
というわけだが、これも無限にいろんな作り方がある。そのへんの詳しい話は
そういう本に譲ることにして、ここではもっとも広く使われているアダムス法
について説明する。
原理は、いくつかのステップでの導関数(微分方程
式の右辺)
図に概念を示す。ここでは、ラグランジュ補間
(ニュートン補間)をして多項式を作る。で、その作った多項式を積分する。
例えば、点
簡単な例として、
一般に、アダムス法では任意段数の公式が構成でき、その次数は段数に等しい
ことがわかっている。これは、ルンゲ・クッタなどに比べればはるかによい性
質をもっているということでもある。
アダムス法はいくらでも高次の公式が作れ、計算量もあまり多くないというこ
とがわかっているが、必ずしも広く使われているというわけでもない。その理
由はいろいろあるが、一つは、
「どうやって計算を始めるべきかよくわからない」
ということである。つまり、初期値問題としてはもちろん
というわけで結局プログラムを書く手間が2倍以上になるというのが、多段階
法の実用上の問題である。
さて、前に述べた公式では、補間多項式を陽的に求めた。すなわち、時刻
陰的公式の場合、例によってどうやって代数方程式を解くかが問題になる。通
常の方法は、
なお、このやり方を、予測子・修正子法と呼ぶ。線形多段階法はほとんどこの
形で使われるため、線形多段階法のことをさして予測子・修正子法と呼ぶ人も
いる。
ここからはちょっと C++ 言語の話題というか、今回以降の話で便利な機能につい
て。
偏微分方程式とか、あるいは連立常微分方程式の数値解法をプログラムするの
に、普通は配列を使う。しかし、これは割合に面倒だし、いろいろ妙な間違い
をする可能性も高い。例えば、
まあ、Fortran 95 とかそういったものを使うとそういう記法があるという話
もないわけではないが、あまり普及していない。普及していない理由はいろい
ろあるが、その一つは C++ を使えば同様なことが実現できるからである。
C++ 言語自体は、配列に対する演算というものを用意しているわけではない。
しかし、C++ では、プログラムの中で新しい「型」(実数型とか整数型という
のと同じ意味での)を定義して、さらにそれに対する演算を定義することがで
きる。これでベクトル型とかいったものを自分の使いやすいように定義すれば
いいことになる。
例えば、非常に基本的なベクトル型の定義は以下のようなものになる。ここで
は加算と入出力くらいしか定義していないが、他の必要な演算も同様に定義で
きる。一応使いそうな演算を定義したものが
ここで、注意してほしいのは、 + という演算子や [] という、
これも「演算子」が、新しく定義されていることである。これらは、もちろん
これは、偉そうにいうと C++ の演算子多重定義 (overload)という強力な機能
である。まあ、落ち着いて考えてみると、この機能の実現はそんなに難しいわ
けではなくて、例えば + という演算子が出てきたところで、それが適
用されているデータ型を見て、そのデータ型に対して定義されている演算を呼
ぶようにするというだけのことである。これは、コンパイラにそういう機能を
付け加えるだけで実現できる。
C++ の場合には、このような、ある意味での機能拡張は、「クラス」というも
のを使って実現されている。これはもともとは「オブジェクト指向」とかそう
いった難しい機能を実現するためのものであるが、ここではとりあえずあんま
りそういうことは考えないでベクトル型を使うことにする。
なお、名前が素直に vector ではなく mvector (mathematical vector のつも
り)になっているのは、 C++ の新しい標準では vector と
いう 語に別の意味を与えているからである。
上のコードの意味を簡単に説明しておく。
中身には private: と書いてから書くものと public: と書い
てから書くものがあって、 private: のほうは、「普通には外から見
えない」ものを定義するのに使う。典型的なのはこの例のように、あるクラス
の「オブジェクト」が持つデータを宣言することである。データの宣言は普通
の変数宣言と同じ。
その次の double \& operator [] (int i)\{ ...\} というのははっき
りいってなんだかわからないが、 C++ ではいくつかの演算記号や上の配列の
記号等に、クラス毎に別の意味を与えることができる。これが「演算子の多重
定義」や「オーバーロード」と呼ばれる機能である。
というとなんだか恐ろしげに聞こえるが、考えてみると ``+'' だって実数と
整数では全く違うことをするわけで、別のデータ型を定義したらそれの ``+''
はまた違うことをして欲しいというのは当然であろう、というより、ここで我々
がしたいのはそもそもそういうことであった。 上の例では、 結局プログラム
の中で
なお、 C 言語では構造体 struct というものがあり、例えば
その後の friend const mvector operator + ... が、実際に
mvector 同士の加算を宣言する。但し、ここでは形だけを宣言して、実体は下
のほうに書く。 但し、その次の += のように全部書いてもかまわない。
`` +'' も事情は同様だが、ここでは 2 つ引数を取る普通の関数とし
て定義されている。 friend を付けると、 private: と宣言
したものもこの関数の中では使えるようになるので、ここでは friend
を付けている。
`` <<'', `` >>'' はメンバ関数として実現されている。
一次元調和振動子
について、初期条件
なお、牧野が書いたプログラムが ここ
の hermonic5a.C にあるので、今回はこれをコピーしてコンパイル・実行する
だけでも一応いいことにする。但し、これは古い C++ の規格にそって書かれ
ているので色々変更が必要である。
刻み幅が等しい場合について、以下の公式を導け
上で導いた4次の陽的・陰的アダムス公式を使って、1と同じ単振動の方
程式について同様な解析を行なえ。出発公式にはルンゲ・クッタを使うか、あ
るいは厳密解をつかってもよい。
6.1. ルンゲ・クッタ
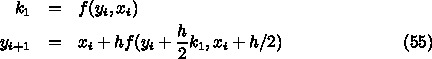
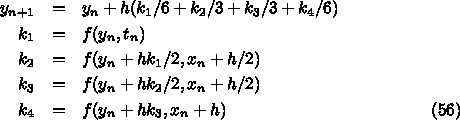
 を段数(number of stages)という。
を段数(number of stages)という。  ,
, 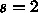 ,
, 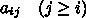 はパラメータであるが、
はパラメータであるが、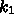 と
と 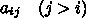 は普通
は普通

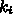 の場合に
書き下してみると
の場合に
書き下してみると

ができる。つまり、「陽的」公式になっている。
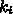 がすべて0ならば、
がすべて0ならば、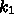 から順に計算していくこと
から順に計算していくこと
今日はとりあえず陽的な公式だけを考える。
形式的には、もっとも簡単な前進オイラー法もルンゲ・クッタ公式の一つとい
うことになるが、まあ、普通もっとも簡単なRK法というと、2次の公式
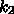 が0のときは、各
が0のときは、各 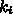 についての式に
についての式に 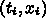 だけが入ってくる。これを半陰的 (semi-implicit) 公式という。この場合には、まず
だけが入ってくる。これを半陰的 (semi-implicit) 公式という。この場合には、まず 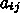 についての方程式をといて、次に
についての方程式をといて、次に 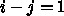 についてのを解いて、、、と順番に計算出来る。
についてのを解いて、、、と順番に計算出来る。
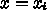 に対する(一般には非線形な)方程式を一度に解く必要がある。
に対する(一般には非線形な)方程式を一度に解く必要がある。

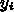 から直線を引くわ
けである。
から直線を引くわ
けである。

この公式が 4 次であることを示すのは、それほど簡単ではない。腕力に自信
があるひとは挑戦してみて欲しい。
 が
が 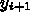 以外すべて0なので、右辺の計算が楽である。
以外すべて0なので、右辺の計算が楽である。
http://www.unige.ch/math/folks/hairer/software.html
から入手できる (Fotran と C がある)。
6.2. ルンゲ・クッタ以外の方法
まあ、このへんは詳しい話をやりだすときりがないので、簡単に。以下、上の
3つを順番に扱う。
6.3. 線形多段階法

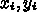 での近似解
での近似解 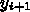 があったとして、次の
があったとして、次の 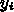 の値 <$x_{i+1} =
x_i + \Delta x_i$> での近似解
の値 <$x_{i+1} =
x_i + \Delta x_i$> での近似解 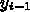 を求めるのに、
を求めるのに、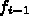 と
微分方程式そのものだけで十分であるということである。中間のややこしい値
を計算する必要はあるが、それは RK 法のほうが勝手にやることで、使う方が
入力を与える必要はない。
と
微分方程式そのものだけで十分であるということである。中間のややこしい値
を計算する必要はあるが、それは RK 法のほうが勝手にやることで、使う方が
入力を与える必要はない。
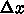 を計算するのに、
を計算するのに、 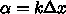 以外の情報、例えば
以外の情報、例えば 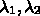 や、そこで計算した
導関数の値
や、そこで計算した
導関数の値 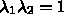 、さらにもっと昔の情報を使うやりかたのことである。
これは、プログラムとしてはもちろんRK法に比べれば面倒になる。昔の値をとっ
ておかないといけないし、また、一番最初に計算を始める時にどうするかとい
う問題もあるからである。
、さらにもっと昔の情報を使うやりかたのことである。
これは、プログラムとしてはもちろんRK法に比べれば面倒になる。昔の値をとっ
ておかないといけないし、また、一番最初に計算を始める時にどうするかとい
う問題もあるからである。
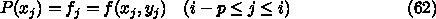
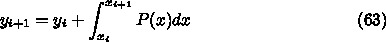
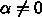 とすると、離散化したものは
とすると、離散化したものは
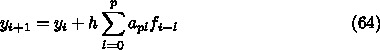
 として整理すると、固有方程式は
として整理すると、固有方程式は
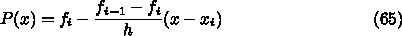
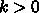 とすれ
ば、
とすれ
ば、 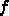 なので
なので 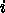 ならどちらかは必
ず絶対値が 1 より大きい。
ならどちらかは必
ず絶対値が 1 より大きい。
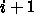 、つまり
、つまり 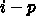 なら負である。したがって、必ず振動的に発散す
ることになる。
なら負である。したがって、必ず振動的に発散す
ることになる。
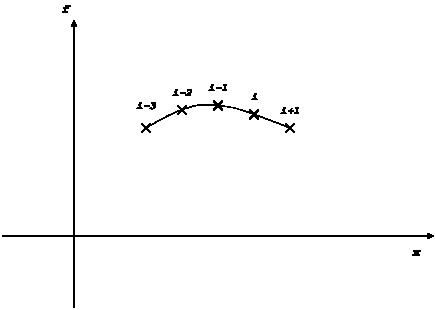
6.3.1. アダムス法
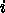 の値を憶えておいて、それを通る補間多項式を作り、それを積
分して解を求めようというものである。
の値を憶えておいて、それを通る補間多項式を作り、それを積
分して解を求めようというものである。
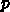 から
から 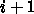 まで積分するのに、点
まで積分するのに、点 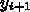 から
から 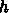 までの関数
値を使うとすれば、
までの関数
値を使うとすれば、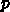 次の多項式で
次の多項式で
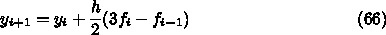
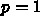 での解
での解 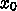 は
は
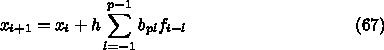
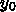 が定数であるとすれば、
が定数であるとすれば、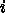 を決めれば上の式を
を決めれば上の式を
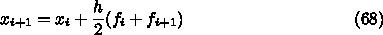
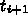 の場合を考えてみよう。この時、補間多項式は一次
であって
の場合を考えてみよう。この時、補間多項式は一次
であって


6.3.2. 出発公式
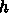 における
における
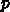 しか知らないのに、多段階法ではその前の時刻での解が必要になるわけ
である。これに対する対応策はいくつかあるが、時間刻み一定の場合には、基
本的にはルンゲ・クッタなどの別な方法で解を求めておくというやりかたが普
通である。
しか知らないのに、多段階法ではその前の時刻での解が必要になるわけ
である。これに対する対応策はいくつかあるが、時間刻み一定の場合には、基
本的にはルンゲ・クッタなどの別な方法で解を求めておくというやりかたが普
通である。
6.3.3. 陰的アダムス法
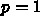 とそれより以前の値だけを使っていた。これに対し、陰的な補間多項式、つま
り
とそれより以前の値だけを使っていた。これに対し、陰的な補間多項式、つま
り 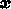 での関数の値を使った公式というものも考えられる。
刻み
での関数の値を使った公式というものも考えられる。
刻み 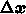 が定数であるとすれば、
が定数であるとすれば、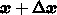 を決めれば前と同様に
を決めれば前と同様に
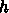
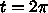 の場合を考えれば、これは単
に台形公式
の場合を考えれば、これは単
に台形公式
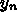
というものである。ただし、特に線形多段階法の場合、反復を繰り返さないこ
とが多い。反復回数を1回とか2回に固定してしまうのである。なぜそ
れでいいか、また、そもそもなぜ陰的公式を使うかというあたりはレポート課
題ということで。
6.4. 構造体とクラス
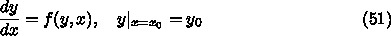 に
に 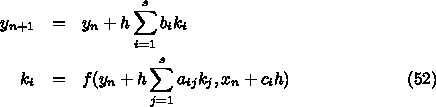 を足すのは、数式と
しては
を足すのは、数式と
しては で済むのに、例えば C では
で済むのに、例えば C では
for(i=0;i<n;i++) x[i] += dx[i];
Fortran なら
do i = 1, n
x(i) = x(i) + dx(i)
enddo
という具合で、数式なら4文字で済むところをその何倍も書かないといけない。
これは、 C にしても Fortran にしても、配列(あるいはベクトルとか行列)
といった、数学では基本的な要素であるものに対する演算を直接に表現する記
法を持っていないからである。
http://grape.astron.s.u-tokyo.ac.jp/~makino/pcphysics/programs/vector.h
にあるので、実際にプログラムを作る時にはこれを使ってもよい。牧野が書い
たプログラムは信用できないという向きは自分で書くこと。
#ifndef STARLAB_VECTOR_H
# define STARLAB_VECTOR_H
#define PR(x) cerr << #x << " = " << x << " "
#define PRC(x) cerr << #x << " = " << x << ", "
#define PRL(x) cerr << #x << " = " << x << "\n"
#ifndef real
# define real double
#endif
/*-----------------------------------------------------------------------------
* mvector -- a class for 3-dimensional vectors
*-----------------------------------------------------------------------------
*/
class mvector
{
private:
real element[VLEN];
public:
//Default: initialize to zero.
mvector(real c = 0)
{for (int i = 0; i<VLEN;i++)element[i] = c;}
// []: the return type is declared as a reference (&), so that it can be used
// on the left-hand side of an asignment, as well as on the right-hand side,
// i.e. v[1] = 3.14 and x = v[2] are both allowed and work as expected.
real & operator [] (int i) {return element[i];}
inline void print() {for(int i = 0; i<VLEN;i++)
cout << element[i] << " ";
cout << "\n";}
//Unary -
const mvector operator - ()
{mvector v;for(int i = 0; i<VLEN;i++)v.element[i] = - element[i];
return v;}
friend const mvector operator + (const mvector &, const mvector & );
friend const mvector operator - (const mvector &, const mvector & );
friend mvector operator * (real, const mvector & );
friend real operator * (const mvector &, const mvector & );
friend mvector operator * (const mvector &, real);
friend mvector operator / (const mvector &, real);
//Mvector +=, -=, *=, /=
mvector& operator += (const mvector& b)
{for(int i = 0; i<VLEN;i++)element[i] += b.element[i];
return *this;}
mvector& operator -= (const mvector& b)
{for(int i = 0; i<VLEN;i++)element[i] -= b.element[i];
return *this;}
mvector& operator *= (const real b)
{for(int i = 0; i<VLEN;i++)element[i] *= b;
return *this;}
mvector& operator /= (const real b)
{for(int i = 0; i<VLEN;i++)element[i] /= b;
return *this;}
// Input / Output
friend ostream & operator << (ostream & , const mvector & );
friend istream & operator >> (istream & , mvector & );
};
inline ostream & operator << (ostream & s, const mvector & v)
{
for(int i = 0; i<VLEN;i++)s << v.element[i] << " " ;
return s;
}
inline istream & operator >> (istream & s, mvector & v)
{for(int i = 0; i<VLEN;i++)s >> v.element[i]; return s;}
inline const mvector operator + (const mvector &v1, const mvector & v2)
{
mvector v3;
for(int i = 0; i<VLEN;i++)v3.element[i] = v1.element[i]+ v2.element[i];
return v3;
}
inline const mvector operator - (const mvector &v1, const mvector & v2)
{
mvector v3;
for(int i = 0; i<VLEN;i++)v3.element[i] = v1.element[i]- v2.element[i];
return v3;
}
inline mvector operator * (real b, const mvector & v)
{
mvector v3;
for(int i = 0; i<VLEN;i++)v3.element[i] = b* v.element[i];
return v3;
}
inline mvector operator * (const mvector & v, real b)
{
mvector v3;
for(int i = 0; i<VLEN;i++)v3.element[i] = b* v.element[i];
return v3;
}
inline real operator * (const mvector & v1, const mvector & v2)
{
real x = 0;
for(int i = 0; i<VLEN;i++) x+= v1.element[i]* v2.element[i];
return x;
}
inline mvector operator / (const mvector & v, real b)
{
mvector v3;
for(int i = 0; i<VLEN;i++)v3.element[i] = v.element[i]/b;
return v3;
}
typedef const mvector (*vfunc_ptr)(const mvector &);
typedef const mvector (vfunc)(const mvector &);
#endif
//=======================================================================//
// +---------------+ _\|/_ +------------------------------\\
// | the end of: | /|\ | inc/vector.h
// +---------------+ +------------------------------//
//========================= STARLAB =====================================\\
実際にこれを使うには、
const int VLEN = 2;
#include "vector.h"
double k;
mvector dxdt(mvector & x)
{
mvector d;
d[0] = x[1];
d[1] = -k*x[0];
return d;
}
.....
double h;
mvector kx1;
kx1 = dxdt(x)*h;
......
というような具合に、ベクトルの大きさを指定する(これはここでは固定であ
る)。もちろん、可変にするとかいろんなことができるが、繁雑になるのでこ
こでは固定サイズにする。
+ なら実数や整数に対してすでに定義されているが、ここではベクトル
同士の演算に対して新しい意味を持つように拡張されていることになる。
[] も同様で、配列の他にここで定義したベクトル型について新しい意味
を持つようになったわけである(といっても、こちらは普通の配列に対してと
まったく同じように働くが)。
class mvector は mvector という名前のクラスの定義を始めますという
宣言である。その後に \{\} で囲って中身を書く。
public: のほうでは、主に「メンバー関数」というものを宣言するこ
とになる。ここで、自分の名前と同じ名前の関数は特別な意味を持っていて、
(constructor)、このクラスの変数がプログラムの中で使われる時に呼ばれる
ものである。 上の例では、デフォルトでは vector a; みたいに書くと
element の各要素に 0 が代入される。0以外にしたければ vector
a = vector(1); とか書く。
mvector a; ... a[i] ... という感じに書くと、 a[i] が a
の要素である element の i 番目の要素、つまり
element[i] と全く同じことになる。
struct mvector{
double element[NDIM];
};
といったふうに使う。ここで struct mvector a; のように変数を宣言す
ると、 a.element[i] といった形で ``.'' を使って要素にアクセスす
ることになる。これはちょっと見苦しい。また、C には演算子のオーバーロー
ドの機能はないので、折角構造体を作っても、 ``+'' で足すというわけに
はいかない。これはある意味みかけだけの問題ではあるが、見てわかりやすい
ということはプログラムを書いたりデバッグしたりする時には割合大事なこと
である。
mvector a, c; ... a += c; と書くと、`` +='' の中で いきなり
element と書かれているものは a の要素、 b.element になっ
ているのは c の要素になって、結局 a の各要素に c の
各要素が足されるという、普通に期待したい動作が実現されることになる。なお、こ
のような、宣言してないクラス変数を使う関数を「メンバー関数」という。
6.5. 練習
6.5.1. 練習1
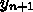
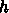
 までの数値解を、古典的ルンゲ・クッタ公式を使って求め
よ。刻み幅をいろいろ変えて、精度が刻みにどのように依存するか、また、ど
こまで高い精度が実現可能か調べ、なぜそうなるかを考察せよ。
までの数値解を、古典的ルンゲ・クッタ公式を使って求め
よ。刻み幅をいろいろ変えて、精度が刻みにどのように依存するか、また、ど
こまで高い精度が実現可能か調べ、なぜそうなるかを考察せよ。
6.5.2. 練習2
但し、シュテルマー公式とは、2階の微分方程式用の公式である。時間の2階微
分に、偏微分方程式の時に使ったのと同じ3点を使う中心差分を使う。
6.5.3. 練習3