./note002.html

ToC

2. ローラー式滑り台の力学 (2023/1/9)

すべり台の動摩擦係数の実測研究 (著者: 村田, 次郎立教大学理学部、塩田, 将基立教大学理学部) というプレプリントが公開されていました。著者の村田氏は立教大学理学部教授で、塩田氏は2021年度の卒業生です。

研究の内容は大変興味深いもので、アブストラクトに

  「重い人ほどすべり台を速く滑るのは何故か」という疑問を動機とし
  た，すべり台の摩擦に関する大学生の探究学習の実践例

とあるように、すべり台を滑る速さと重量の関係を調べ、その原因を検討したものです。以下、これを「村田・塩田論文」と書きます。(あるいは単に「論文」)

なお、滑り台といっても、小さな公園によくあるステンレスとかの板の滑り台ではなく、ローラー式というもので、滑るところが板ではなくて直径数センチのローラーが並んでいるものです。例えばここに写真と図面があります。

普通の滑り台だと、重力で滑るためには動摩擦力より重力の滑り台に平行な方向の分力が大きい必要があり、かなり傾斜が大きいものでなければなりません。さらに、その時には一定の加速度でずっと加速が続くわけなので、あまり長いものはつくれそうにありません。

ところが、ローラー式だとずっと抵抗が小さいので、小さな傾斜で長いものを作ることができ、実際に非常に長い、100mを超えるようなものが設置されているようです。そうすると、どんどん加速していって危ないのでは?という気もするのですが、そういうこともないようです。なので、ローラー式滑り台については、村田・塩田論文の疑問である「重い人ほどすべり台を速く滑るのは何故か」の他に、「長い滑り台ではどんどん加速してしまわないのか」というもうひとつの疑問があります。

村田・塩田論文では、まず、実際にローラー式滑り台に色々な重量のものをのせて、速度を計測しています。これは極めて科学的で素晴らしいアプローチです。その結果は論文の図1に示されており、 1kg-6kg 程度のものでは、

数メートル滑ると速度がほぼ一定になる
その速度は重いほど大きい

ことが明確に示されています。定常になった速度は論文には記述されていませんが、図5の K1 の値と3式の後の終端速度の式から 0.58m/s であることがわかります。他の重量の場合もまとめると以下のようになります。

 重量(kg)  K      終端速度(m/s)  1kg の時の速度との比  質量の平方根
 1         0.395    0.58                  1               1
 2.2       0.255    0.905               1.55            1.48
 4.2       0.175    1.32                2.25            2.05
 6.2       0.145    1.59                2.72            2.49

4列めは、1kg の時の速度に対して何倍になっているか、という速度比で、 5列目は質量の平方根です。この2つは 10% 程度の差で、終端速度は概ね質量の平方根になっていることがわかります。

つまり、実験的には、「重い人ほどすべり台を速く滑るのは何故か」と「長い滑り台ではどんどん加速してしまわないのか」の2つの疑問に対して、まず実際に重いものは速く滑り、これは終端速度が重量の平方根に比例する、と表現できる。このため、長い滑り台でもどんどん加速していくことはない、ということが確認されたわけです。これは卒業研究として素晴らしいものだと思います。

すると、残る疑問は、ではなぜ終端速度は重量の平方根に比例するのか?ということです。論文では、

  重いほどすべり台を速く滑る理由は直接的には，ローラー式すべり台
  の動摩擦係数には速度依存性があり，かつ，同じ速度では重い方が動
  摩擦係数が小さくなる傾向がある為と考える事が合理的である。

と、「ローラー式すべり台の動摩擦係数」がそのようなものであるから、としています。ここでは、より単純な説明を試みます。それは、

  ローラーの回転の運動エネルギーにいく分を考慮する

というものです。まず、なぜこれを考慮するか、ですが、終端速度を考慮するとローラーの回転エネルギーは無視できないからです。

論文には、滑り台の角度は 13度、ローラーは直径18mmのアルミ棒で間隔 25mm とあります。滑り台の幅は書いてありませんが、典型的なものと思われる 60cm としましょう。滑り台の角度を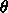、ローラーの半径、幅、間隔をそれぞれ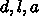、比重を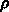とするとローラー1本の質量は

であり、単位長あたりの質量は

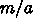で、それぞれ 0.412kg, 16.5kg/m となります。実験での速度は 1m/s 程度、物体の質量は 1-10kg 程度なので、1秒滑る時に自分より重いローラーを回転させているわけです。

ここで、非常に単純に、終端速度で、物体が滑りおりたことによる位置エネルギー変化が全てローラーの回転エネルギーに変換されたとしてみます。すると、円柱の慣性モーメントは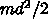なので、滑る物体の質量を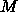、重力加速度を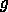、終端速度をとすると、単位時間あたり変換される位置エネルギーは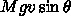、単位時間あたり回転を始めるローラーは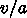本、一本のローラーの回転エネルギーは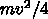なので

となり、

で、実際の数値をいれると SI 単位系で

となります。実際の係数は 0.73 ではなく 0.58 だったので非常によくあっているとはいえませんが、かなり近いことがわかります。

つまり、非常に雑に「エネルギーは全部ローラーの回転エネルギーになる」という近似をしても、物体の重量 1-6kg で3倍ほど変わる実験結果を25%程度の精度で説明できる、ということになります。

とはいえ、だからこれは本当か、というと、少なくとも2つ問題があります

ローラーは中実のアルミ棒ではなくて、パイプにして強度的に問題ない範囲で原価を下げていると思われる
ローラーは最初の物体との接触時点では回転していないため、接触面は必ず滑って加速される。この間は滑ることによる損失があるため、エネルギーの一部しか回転エネルギーに変換されない。

他にも、細かいことを考えるとローラーと軸受との摩擦損失はどうなってるかとか、接触した時にローラーは回転の他荷重をうけた変形もするはずで、そっちにいくエネルギーはどうかとか色々ありますが、上のもっとも単純な近似で大体説明できる、ということからもこれらの項の寄与は小さいのではないかと想像されます。

実際には、軸受との摩擦損失は多分無視できません。それが通常の動摩擦係数に近い、負荷質量に比例する振舞いなら実効的な重力定数を小さくするので、確かに速度を小さくします。また、負荷質量に比例しない定数項的なものがあれば、物体の重量が非常に小さい時に重量の平方根よりも速度が遅くなることを説明できます。

以下、上の 2の効果、つまり、ローラーを加速する間の損失を検討します。

ローラーを力 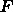(本当はトルクですが本質的に同じなので)一定で加速すると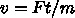で秒後の運動エネルギーは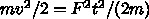となり、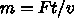を使ってを消すと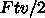となります。一方その速度で始めから動いていたものの仕事は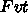なので、仕事のちょうど半分がローラーの運動エネルギーになります。これを考慮すると

で、実際の数値をいれると SI 単位系で

で、今度はちょっと小さくなりすぎます。一方で、ローラーがパイプであれば慣性モーメントはある程度減るので、その効果をいれると非常によく実験結果を説明できるのかもしれません。これは、実験に使われたローラーの構造、重量について情報が欲しいところです。

まとめると、本稿での検討からは、ローラー式滑り台での物体の終端速度はかなりよい精度で物体の質量の平方根に比例し、これは物体が滑っていく時にローラーに運動エネルギーを与える、ということによって説明できる、ということがいえたことになります。動摩擦係数が速度や質量に依存する、というような効果を導入する必要はありません。

なお、このような、終端速度がローラーの回転エネルギーによって説明できるのでは、という考察はツィッター上では @HK_G3A3、@litulon、@hzmik、 @llewkcor2178 といった複数の方が独立にしておられました。また、ローラーが軽いという指摘は論文著者の1人である @jiromurata からいただきました。ここで感謝いたします。

Previous ToC Next