 で計算でき、全粒子へ
の力であればその
で計算でき、全粒子へ
の力であればその 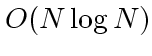 で計算できることになる。
で計算できることになる。
計算量を減らすには、遠くの粒子を適当にまとめたい。例えば
遠くの方の粒子のかたまりをそれらの重心で置き換えてもいいし、高い精度が
必要なら多重極展開も考えられる。遠くにいくに従ってかたまりを大きくして
いけば、直観的には一つの粒子への力を  で計算でき、全粒子へ
の力であればその
で計算でき、全粒子へ
の力であればその ![]() 倍の
倍の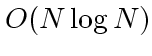 で計算できることになる。
で計算できることになる。
もちろん、ここで問題なのはどうやってうまく粒子をかたまりに分けるかとい
うことである。ある粒子への力を計算するのに適した分け方を見つけるには、
すくなくとも一度は全粒子をみないといけない。従って、その計算量は
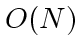 より小さくはない。粒子毎に別の分け方をしたら、それだけで計算量
が
より小さくはない。粒子毎に別の分け方をしたら、それだけで計算量
が 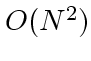 になってしまう。
になってしまう。
この問題は、すべての粒子に使える汎用の分け方というのをあらかじめ構成す ることができれば解決する。それをするのがツリー構造による階層的な空間分 割ということになる。
図で説明しよう。3次元の図は書きにくいし見る方も見にくいであろうから、2 次元で書くことにする(図1)。まず、平面内の適当な領域に粒子が分布して いるとしよう。粒子が有限個なので、そのすべてを含む正方形を考えることが 出来る。すべて含んでいればよいので、別に最小である必要はないが、大きく ても無駄なだけなので普通はそこそこ小さくとる。これを、まず4つの小正方 形(セル)にわける。で、そのそれぞれをさらに4つにわけるというのを再帰的 に繰り返していく。
粒子が0個または1個しかなくなったところで止める。この
空間(平面)分割に対応したツリー構造を考えると、根に全体の正方形に対応
する節点があり、その下に4つの小正方形、さらにその下にそのそれぞれの中
の4つ![]() と続いていって、ツリーの葉には粒子1つ1つがくることになる。
この方法では、粒子の数密度が高いところでは細かく、そうでないところでは
粗いという意味で、適応的な構造が実現されていることに注意してほしい。
3次元にすれば、正方形4個の代わりに立方体8個となるが、それ以外は全く同
じである。
と続いていって、ツリーの葉には粒子1つ1つがくることになる。
この方法では、粒子の数密度が高いところでは細かく、そうでないところでは
粗いという意味で、適応的な構造が実現されていることに注意してほしい。
3次元にすれば、正方形4個の代わりに立方体8個となるが、それ以外は全く同
じである。
次に、どうやってこのツリー構造を使って一つの粒子への重力が計算できるか
ということを考えてみる。このためには、ツリーのある節点が表す立方体内の
粒子全体からのある粒子への力を計算する方法を与えればよい。(なお、以下
では、節点に対応する立方体、あるいはそのなかの粒子全体のことも単に節点
ということがある)系全体からの力は、単に根節点からの力として計算できる。
一つの節点からの力を以下のように計算することにする
 |
 |
ツリー法を実際に使うには、各節点についてその中の粒子全体の重心の位置と 質量(あるいは多重極展開の展開係数)をあらかじめ求めておく必要がある。 これらはやはり再帰的に定義することができる。つまり、子節点の中の粒子全 体の重心の位置と質量がわかっていれば、親節点の情報は計算できる。多重極 展開の展開係数についても(計算は繁雑であるが原理的には)おなじことであ る。