


Next: 5 次週予告
Up: 計算天文学 II
Previous: 3 プログラム
1と2は必須。後はオプション。 2 についてはプログラムリストも提出
すること。
- 空間方向の2階微分の近似式 (4) が実際に2階微分の近
似になっている(
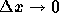 の極限で2階微分に収束する)こ
とを証明せよ。
の極限で2階微分に収束する)こ
とを証明せよ。
- 初期条件が
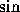 関数
関数 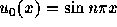 である時の厳密解
を求めよ。さらに、例のプログラムを変更し、n=1 の場合の数値解をもとめ、
t=1 の時の厳密解との差(誤差)の最大値を
である時の厳密解
を求めよ。さらに、例のプログラムを変更し、n=1 の場合の数値解をもとめ、
t=1 の時の厳密解との差(誤差)の最大値を 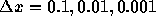 の場合について求めよ。なお、
の場合について求めよ。なお、 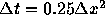 とする
こと。さらに、求まった結果がなぜそうなるかを考察せよ。
とする
こと。さらに、求まった結果がなぜそうなるかを考察せよ。
- さらに、
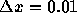 の場合について、誤差を時間 t の関
数としてプロットせよ。誤差は時間のどのような関数か?またなぜそうなるか
考察せよ。
の場合について、誤差を時間 t の関
数としてプロットせよ。誤差は時間のどのような関数か?またなぜそうなるか
考察せよ。
-
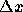 の値を固定し、
の値を固定し、 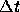 の値をいろいろ変えてみて数
値解がどうなるか調べよ。また、なぜそうなるか考察せよ。
の値をいろいろ変えてみて数
値解がどうなるか調べよ。また、なぜそうなるか考察せよ。
- 例題のデルタ関数の場合について、2,3と同様に厳密解と数値解の差を求
めよ。
- 固定境界条件の他、周期境界条件 [
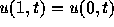 ] も扱えるよう
にプログラムを変更し、
] も扱えるよう
にプログラムを変更し、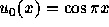 の場合の数値解を求めてみ
よ。
の場合の数値解を求めてみ
よ。
-
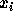 の両側 1点だけでなく 2 点ずつ使う差分式を講義で説明した方
法で導け。
の両側 1点だけでなく 2 点ずつ使う差分式を講義で説明した方
法で導け。
- 周期境界の場合に、上の差分式をプログラムにして計算精度を簡単な公
式と比較せよ。刻み幅が同じ時に精度は良くなっているか?またそれは何故か
考察せよ。
- 拡散係数が空間座標 x に依存する場合に、拡散方程式自体を導け。
- 拡散係数が空間座標 x に依存する場合に、空間差分式はどのような
ものになるか検討せよ。
Jun Makino
Wed Oct 11 11:55:04 JST 2000
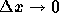 の極限で2階微分に収束する)こ
とを証明せよ。
の極限で2階微分に収束する)こ
とを証明せよ。
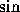 関数
関数 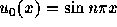 である時の厳密解
を求めよ。さらに、例のプログラムを変更し、n=1 の場合の数値解をもとめ、
t=1 の時の厳密解との差(誤差)の最大値を
である時の厳密解
を求めよ。さらに、例のプログラムを変更し、n=1 の場合の数値解をもとめ、
t=1 の時の厳密解との差(誤差)の最大値を 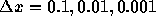 の場合について求めよ。なお、
の場合について求めよ。なお、 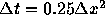 とする
こと。さらに、求まった結果がなぜそうなるかを考察せよ。
とする
こと。さらに、求まった結果がなぜそうなるかを考察せよ。
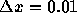 の場合について、誤差を時間 t の関
数としてプロットせよ。誤差は時間のどのような関数か?またなぜそうなるか
考察せよ。
の場合について、誤差を時間 t の関
数としてプロットせよ。誤差は時間のどのような関数か?またなぜそうなるか
考察せよ。
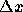 の値を固定し、
の値を固定し、 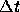 の値をいろいろ変えてみて数
値解がどうなるか調べよ。また、なぜそうなるか考察せよ。
の値をいろいろ変えてみて数
値解がどうなるか調べよ。また、なぜそうなるか考察せよ。
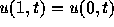 ] も扱えるよう
にプログラムを変更し、
] も扱えるよう
にプログラムを変更し、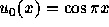 の場合の数値解を求めてみ
よ。
の場合の数値解を求めてみ
よ。
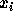 の両側 1点だけでなく 2 点ずつ使う差分式を講義で説明した方
法で導け。
の両側 1点だけでなく 2 点ずつ使う差分式を講義で説明した方
法で導け。