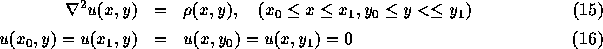
ただし、 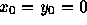 ,
, 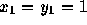 としてよい(入力パラメータとして読め
る汎用的なプログラムを作ってくれればもちろんそのほうがよい)。
さらに、
としてよい(入力パラメータとして読め
る汎用的なプログラムを作ってくれればもちろんそのほうがよい)。
さらに、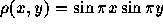 として、初期推定
として、初期推定 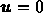 から出発した時に
から出発した時に
- 残差
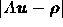 が反復を繰り返した時にどのように 0に近付くか
が反復を繰り返した時にどのように 0に近付くか
- 収束した時に、真の解との差(誤差)はどうなっているか
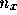 (
(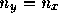 としてよい) のいくつかの値について調べ、そ
れから精度が
としてよい) のいくつかの値について調べ、そ
れから精度が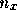 の何乗になっているか議論せよ。
の何乗になっているか議論せよ。
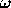 の値は
の値は
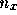 に依存するかどうかも議論すること。
に依存するかどうかも議論すること。
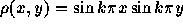 (kは整数)の時に、誤差は
どうなるか、理論的または数値的(両方あればそれもOK)議論せよ。
(kは整数)の時に、誤差は
どうなるか、理論的または数値的(両方あればそれもOK)議論せよ。
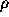 がデルタ関数
がデルタ関数 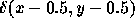 の時に、厳密解をフーリ
エ級数の形で表せ。
の時に、厳密解をフーリ
エ級数の形で表せ。
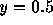 の線上で誤差が
どのように分布するか調べよ。また、誤差の等高線表示や3次元表示を適当な
ツールを使って作ってみよ。(PGPLOT には等高線表示をするサブルーチンが準
備されている)
の線上で誤差が
どのように分布するか調べよ。また、誤差の等高線表示や3次元表示を適当な
ツールを使って作ってみよ。(PGPLOT には等高線表示をするサブルーチンが準
備されている)