1 最適化

今日と来週で最適化の話をして、最後ではデータ構 造の話を最後にやることにしたい。

で、最適化であるが、これは天文学の観測・理論のあらゆる場面で必要になる とても重要な技術である。

現代の天文学の観測においては、例えばなにかを観測してデータをとったとし て、それから実際に天文学的に意味があることをいうまでにはいろいろなステッ プがはいるのが普通である。多くの場合に、これはいろいろな自由パラメータ があるモデルを持ってきて、そのモデルのパラメータを観測データを「もっと もうまく説明する」ように決めるということである。例えば銀河内のガスの速 度から質量分布を推測するとか、銀河団ガスからのX線放射から質量を推定す るといった場合には、結局そういうことをやっているわけである。もっともう まく説明するとは、具体的にはなんらかの形で誤差を表現して、 それを最小化するということである。

これは、まあ、形式的には例えばこういうふうな話になる：

「ある領域 $D$ 上で定義された実数値関数 $f(x)$ がある。その最小値とそれ を与える $x \in D$ を求めよ」

つまり、最適化というのは要するにこういう話である。

とはいえ、実際にどうやって上の問題の答を求めるかというのは、もちろん領 域 $D$ がどんなものかと関数 $f$ がどんなものかによる。例えば、観測デー タを線形回帰して直線近似するなら、$D$は直線 $y=ax+b$ の係数$(a,b)$ の 集合ということになろう。 $f$ は2乗残差である。これは2次形式の最小化に なり、微分すれば連立一次方程式が出てきて解ける。パラメータの数が多くて も、2次形式なら話は同じである。

これに対して、同じような多次元空間内の最適化でも、もとの関数がどんなも のか良くわからないとか、計算が面倒であるとかいうと、急に話がややこしく なる。

例えば、次の図は連星重力レンズと推定されたものの観測結果と、それのモデ ルである。

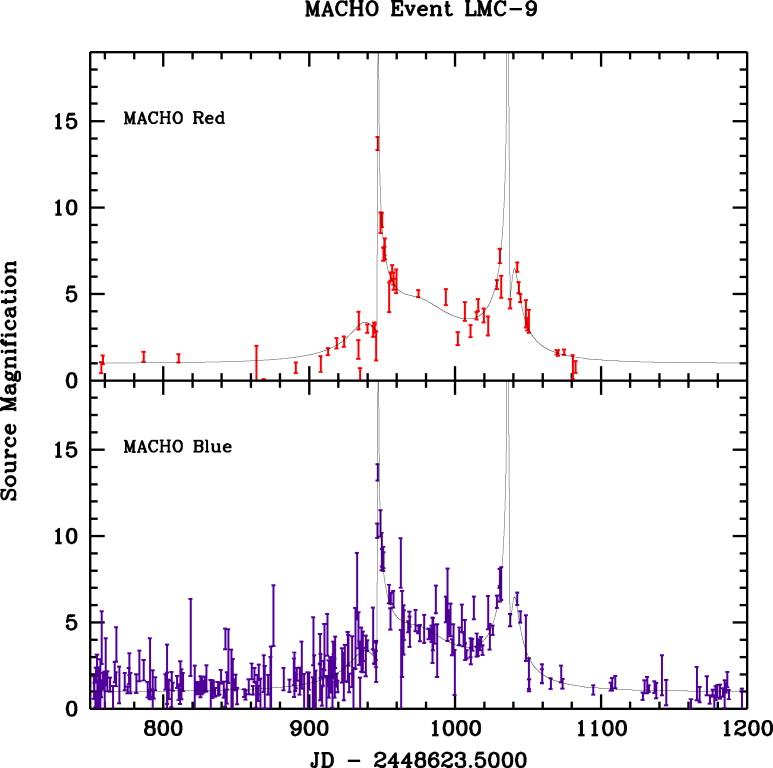
横軸は時間、縦軸は明るさである。連星レンズの特徴は、単一星の場合と違っ てピークが2つできることと、そのピークが単一星のばあいよりもずっと明る いことである。

連星レンズの場合、パラメータの数は非常に多い。連星自体の軌道要素が 6 個、その他に質量比、周期、光源の速度、それぞれの我々からの距離というこ とで10個以上ある。なお、このうちいくつかは縮退しているので、本当のパラ メータは9個である。で、どのパラメータを変えるとなにがどう変わるかとい うのは簡単にはわからない。こういう時に、どうやってレンズのライトカーブ の観測から、物理的な意味を引き出せるのだろうか？

というわけで、世の中には多様な最適化手法がある。これらを簡単にまとめる のが今日の話ということになる。