前回は、まず、恒星系を分布関数
![]() で表現する、というところか
ら始めた。この
で表現する、というところか
ら始めた。この ![]() を質量分布関数だと思うと、速度空間でこれを積分すると
質量密度
を質量分布関数だと思うと、速度空間でこれを積分すると
質量密度 ![]() になり、重力ポテンシャル
になり、重力ポテンシャル![]() は
は
| (1) |
で、まず重要なのは、力学平衡状態、つまり ![]() が時間進化しないで、上の2
つを連立させたものの解になっているケースである。力学平衡状態については
ジーンズの定理が成り立ち、
が時間進化しないで、上の2
つを連立させたものの解になっているケースである。力学平衡状態については
ジーンズの定理が成り立ち、 ![]() が与えられたポテンシャルの中での運動の
積分、つまり軌道のエネルギーや角運動量といった保存量で書ける。
が与えられたポテンシャルの中での運動の
積分、つまり軌道のエネルギーや角運動量といった保存量で書ける。
このことから、基本的な例として球対称な恒星系を考えると、 ![]() がエネル
ギーと全角運動量だけの関数になることがわかる。さらに簡単な場合として、
がエネル
ギーと全角運動量だけの関数になることがわかる。さらに簡単な場合として、
![]() がエネルギーだけの関数、というものを考える。
がエネルギーだけの関数、というものを考える。
これは速度分布が等方的、ということに対応していて、それほど変な仮定では ない。
そうすると、球対称のポアソン方程式に、密度は ![]() を速度空間で積分した
もの、というのをいれて、さらに
を速度空間で積分した
もの、というのをいれて、さらに
| (3) |
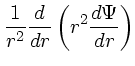 |
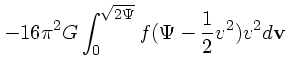 |
||
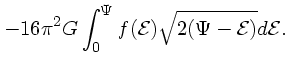 |
(4) |