3 自己相似解の後の進化

さて、自己相似解は、ある時刻 $t_0$ で密度が無限大になる。これを collapse と呼んでいる。実際にそんなことが起きるのか、また、そのあとは どうなるのかというのは現実的には重要な問題である。というのは、多くの球 状星団、あるいは dwarf E では、タイムスケールを見積もるとすでに collapse しているはずだからである。

その後どうなるかについては、いろんな可能性が考えられた。特に、これによっ てブラックホールを作るというアイディアはそれなりに真剣に検討された。

現在のところ、典型的な球状星団とか dwarf E では、ブラックホールが出来 るというのはありそうにない。コアが十分に小さくなると、エネルギー供給源 が出来るからである。

ここでのエネルギー供給の元は連星である。仮に星団があらかじめ連星をもっ ていなかったとしても、コアが十分に小さくなると、そのなかで3体相互作用 で連星ができるようになる。これは基本的には星のなかで温度、密度が上がる と核融合が始まるというのと変わるところはない。ただし、量子力学的な効果 はないので、連星の出来やすさは密度と温度（平均速度）の関係だけで決まる。

連星によるエネルギー供給が入ると、コアの収縮は止まる。熱源として連星を 考えた計算を始めて行なったのは Henon (1975) であり、1982年ころまでにい くつかそのような計算が行なわれた。それらでは、コアからの熱伝導による熱 の流出と連星からのエネルギー入力がバランスし、系全体がホモロガスな膨張 をするという結果が得られていた。特に、 Goodman (1984) は実際にそのよう なホモロガスな解を求めた。

しかし、 1983 年になって、 Sugimoto & Bettwieser は、実はこのホモロガ スな膨張解も熱力学的に不安定であるという発見をし、その結果起きる振動に 「重力熱力学的振動」という名前をつけた。

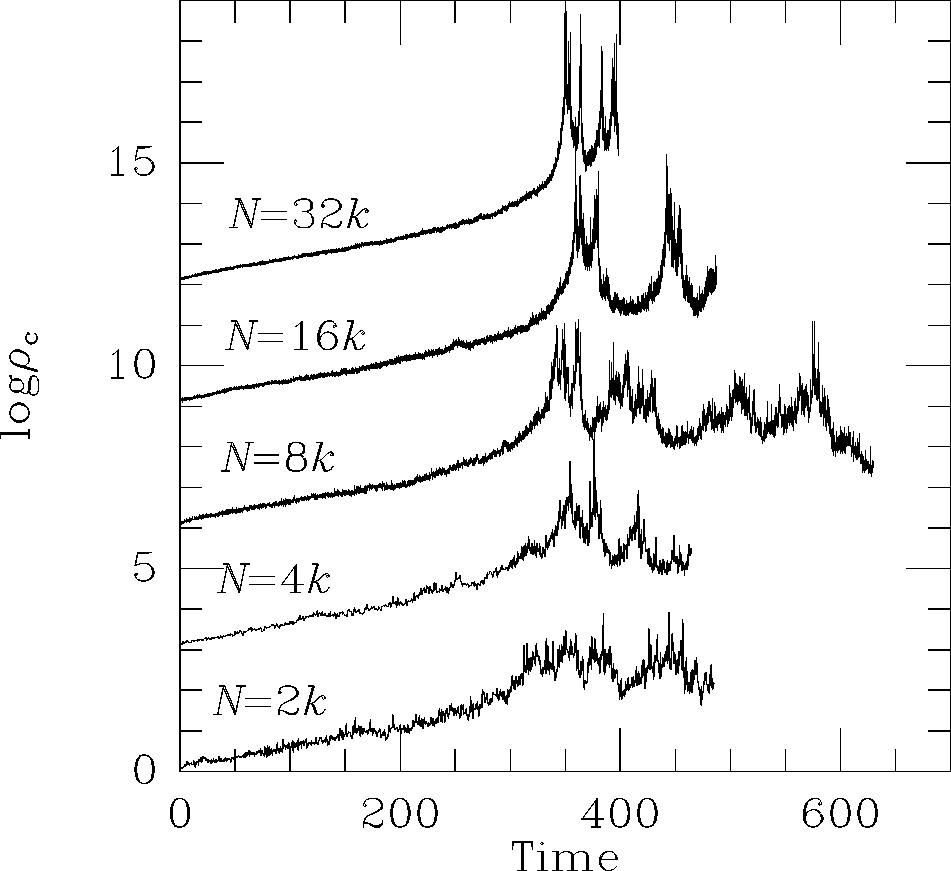
以下に示すのが彼らの見いだした振動の様子である。

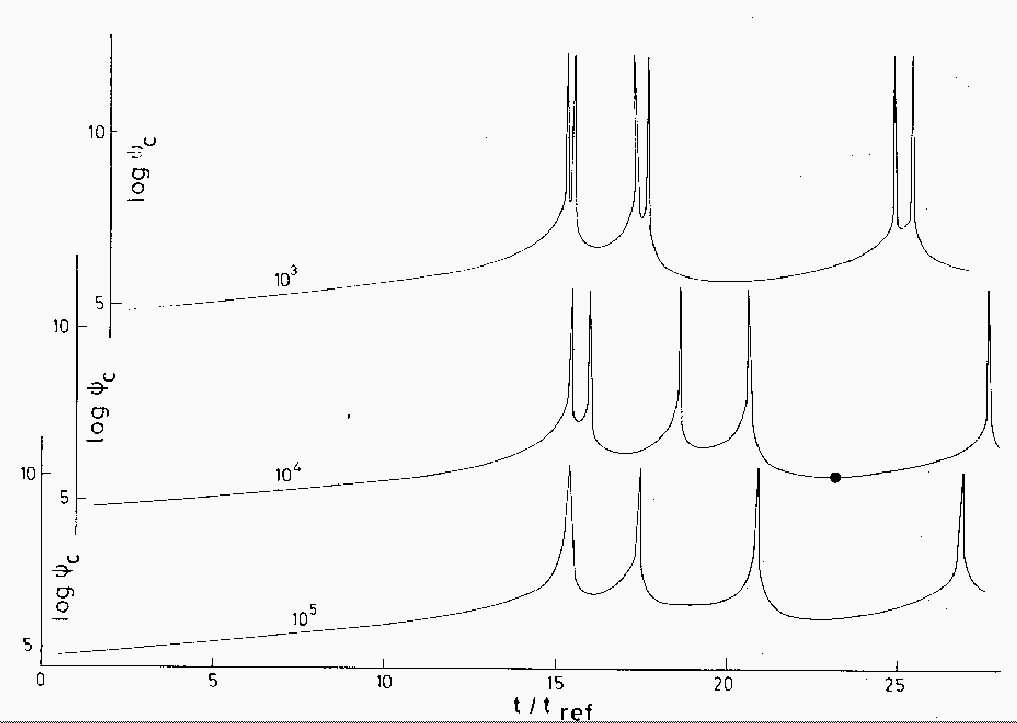
まず、この図は中心密度の時間変化である。3本線があるのは、エネルギー生産の係数である。小さいほうがより振動の振幅が大きくなっているのがわかる。

5cm

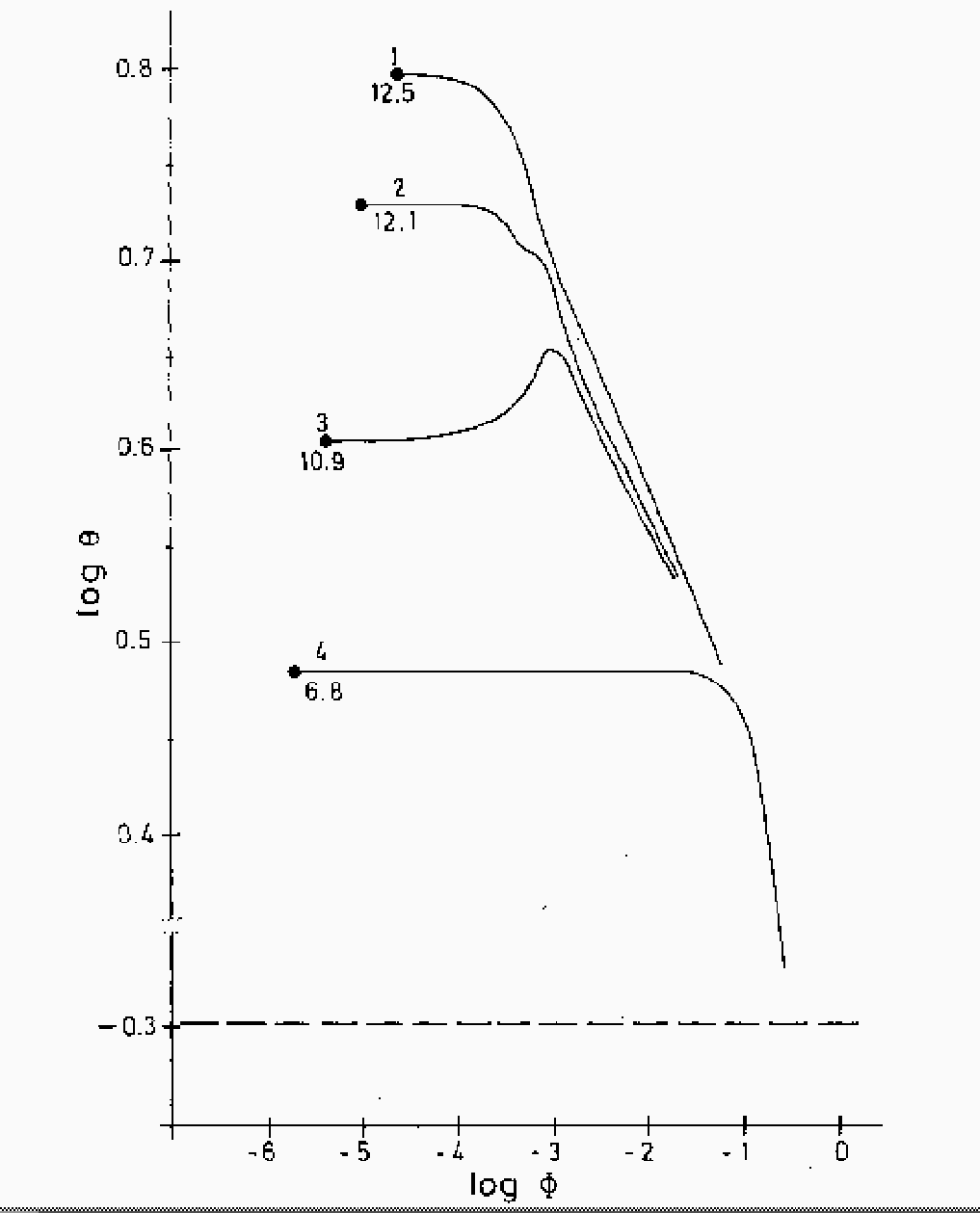
これは膨張中の温度分布の変化。注意して欲しいのは、膨張中(3番の線)では、 温度のピークがコアの外側にあることである。このような温度の逆転があるこ とで、コア付近では熱が外側から内側に流れることが可能になる。この時には、 等温状態の線型解析で膨張に対しても不安定であったのと同じように、熱が流 れこんで膨張することで一層温度が下がり、さらに熱が流れこむ。

5cm

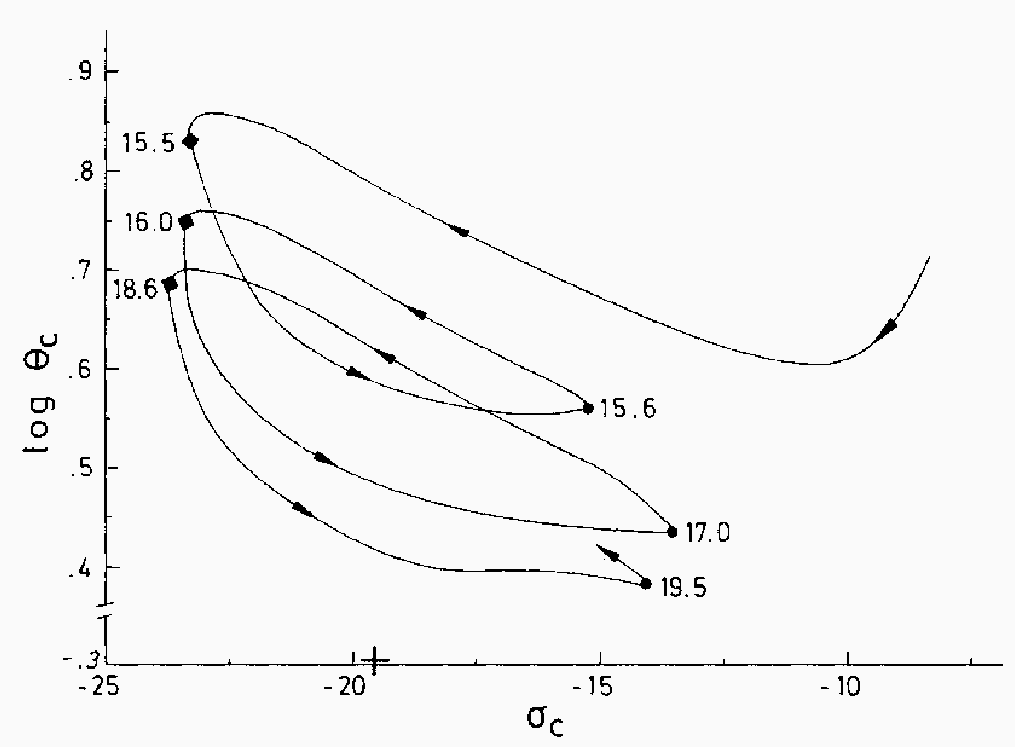
最後に、これはエントロピーと温度の平面でのコアの軌跡である。注意して欲 しいのは、この軌跡はこの平面で反時計回りになっていることである。これは どういう意味があるかを考えてみる。

カルノーサイクルはこの平面上で長方形だが、熱機関は時計回りである。この時に、 $\Delta Q = T\Delta S$ を積分して正になって元に戻るので、外への仕事 $\Delta W$ は $\Delta Q$ と等しく正になる。熱機関であるとはそういうこ とであった。

これに対して逆に回るとは、冷凍機(ヒートポンプ)のサイクルになっているこ とに対応する。つまり、低温の時に吸収した熱を高温になってから放出してお り、そのために外からの仕事を利用している。このことは、この振動が本質的 に熱力学的な不安定性によって起きているということを意味している。

もしも単に連星のエネルギー生産が密度が上がると始まり、密度が下がると止 まるということで振動が起きているとすると、この時にはコアの軌跡は熱機関 的になるはずである。そうではないということが現象を理解する上では極めて 重要なことであった。

5cm

とはいえ、彼らの結果はただちに広く受け入れられたわけではなく、 そのあと数年に渡る論争があった。その理由は、「それまでの他の人の計算で はいずれも振動が起きていなかった」ためである。具体的には、フォッカープ ランク方程式を解く計算、ガスモデルでの計算、また、フォッカープ ランク方程式をモンテカルロ法で解く計算のいずれでも振動は起きていなかっ た。また、直接の多体計算では、計算機の能力が不足で振動がはっきり見える 粒子数を扱うことがそもそもできなかった。

が、1985 年には他のグループによるガスモデル計算、1986年には FP計算でも 振動が確認された。このきっかけになったのは、 1984 年の IAU Symposium No. 113 であり、ここで杉本が D. C. Heggie と議論し、 Heggie の流体コー ドの出力を見て、「時間ステップが大き過ぎるのではないか」と指摘した。

すなわち、自己重力質点系の流体モデルの計算では、それまでのほとんどの計 算で、時間刻みは可変であったものの、「1ステップでの変化がある程度以上 大きくならないようにする」という基準での時間刻みが使われていた。しかし、 この基準での時間刻みと、熱伝導を安定に解く数値計算法を組み合わせると、 結果として本来不安定な系でも数値解は安定になってしまうという問題が発生 する。

杉本は、元々恒星の内部構造の研究者であり、特に様々な熱的不安定の数値シ ミュレーションを行ってきたのでこれらの点には注意深かった。このために、 元々 Bettwieser の数値計算で振動が起こった時にその結果に「正しい」解釈 を与えることができたのである。

さらに、 1987年には Goodman が自分の求めたホモロガスな 膨張解の安定性解析を行い、粒子数が大きい(正確にはエネルギー生産の密度 依存性の係数が小さい)と膨張解が不安定になることを示した。

実際に粒子系でそんなものが起きるかどうかにはさらに議論があったが、1995 年になって$N$体数値計算でも確かに振動が起きるということが見い出された。

7cm