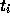 における解
における解 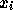 がわかっていれば、それだけ
から次の時刻
がわかっていれば、それだけ
から次の時刻 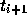 での解
での解 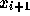 が求まるものである。
が求まるものである。
これまでの数回で、広く使われている公式の一つであるルンゲ・クッタ型公式 についてその原理と実例を簡単に説明した。今日は、同様に広く使われている 公式である線形多段階法についてその原理をまとめる。
ルンゲ・クッタ法は「一段階法」と呼ばれるクラスに属する。一段
階法とは、ここでは、 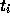 における解
における解 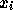 がわかっていれば、それだけ
から次の時刻
がわかっていれば、それだけ
から次の時刻 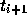 での解
での解 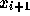 が求まるものである。
が求まるものである。
これに対し、 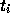 での情報だけでなく、その前のステップでの情報(導関
数の値や解そのものの値)を記憶しておいて、それを使おうというのが多段階
法である。これにより、余計な計算をしないで計算精度をあげようというわけ
である。
での情報だけでなく、その前のステップでの情報(導関
数の値や解そのものの値)を記憶しておいて、それを使おうというのが多段階
法である。これにより、余計な計算をしないで計算精度をあげようというわけ
である。
線形多段階法のなかでもっとも広く使われているのは、アダムス法といわれる クラスの公式である。この原理は、いくつかのステップでの導関数(微分方程 式の右辺) fの値を憶えておいて、それを通る補間多項式を作り、それを積 分して解を求めようというものである。
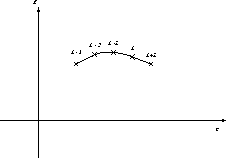
上の図に概念を示す。ここでは、前回の積分公式と同様にラグランジュ補間 (ニュートン補間)をして多項式を作る。で、その作った多項式を積分する。 例えば、点 i から i+1まで積分するのに、点 i-p から iまでの関数 値を使うとすれば、p次の多項式で
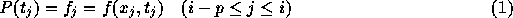
を満たすものを作る。で、i+1での解 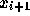 は
は

で与えられる。 刻み hが定数であるとすれば、pを決めれば上の式を

の形に書き直せる。
簡単な例として、 p = 1の場合を考えてみよう。この時、補間多項式は一次 であって
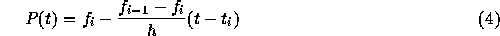
となって、これを積分すれば、結局

となる。
一般に、アダムス法では任意段数の公式が構成でき、その次数は段数に等しい ことがわかっている。これは、ルンゲ・クッタなどに比べればはるかによい性 質をもっているということでもある。
アダムス法はいくらでも高次の公式が作れ、計算量もあまり多くないというこ とがわかっているが、必ずしも広く使われているというわけでもない。その理 由はいろいろあるが、一つは、
「どうやって計算を始めるべきかよくわからない」
ということである。つまり、初期値問題としてはもちろん 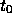 における
における
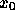 しか知らないのに、多段階法ではその前の時刻での解が必要になるわけ
である。これに対する対応策はいくつかあるが、時間刻み一定の場合には、基
本的にはルンゲ・クッタなどの別な方法で解を求めておくというやりかたが普
通である。
しか知らないのに、多段階法ではその前の時刻での解が必要になるわけ
である。これに対する対応策はいくつかあるが、時間刻み一定の場合には、基
本的にはルンゲ・クッタなどの別な方法で解を求めておくというやりかたが普
通である。
というわけで結局プログラムを書く手間が2倍以上になるというのが、多段階 法の実用上の問題である。
さて、前に述べた公式では、補間多項式を陽的に求めた。すなわち、時刻 i
とそれより以前の値だけを使っていた。これに対し、陰的な補間多項式、つま
り 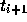 での関数の値を使った公式というものも考えられる。
刻み hが定数であるとすれば、pを決めれば前と同様に
での関数の値を使った公式というものも考えられる。
刻み hが定数であるとすれば、pを決めれば前と同様に

の形に書けることになる。また手をぬいて p=1の場合を考えれば、これは単 に台形公式

となる。
陰的公式の場合、例によってどうやって代数方程式を解くかが問題になる。通 常の方法は、
なお、このやり方を、予測子・修正子法と呼ぶ。線形多段階法はほとんどこの 形で使われるため、線形多段階法のことをさして予測子・修正子法と呼ぶ人も いる。
線形多段階法の誤差の問題を考えるには、補間多項式の主要誤差が陽的公式と
陰的公式でどう違うかということを考える必要がある。線形多段階法の、特に
大域誤差の理論は難しいので、以下局所誤差について考える。局所誤差を考え
る時に、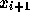 以外の値には数値誤差を含まないとして考える。この扱い
でとりあえず大体のことはわかる。
以外の値には数値誤差を含まないとして考える。この扱い
でとりあえず大体のことはわかる。
一般に、厳密解は独立変数 tによるテイラー展開を持つとしてよいので、 p次の補間多項式で近似したときの主な誤差は p+1次の成分から出てくる。
補間多項式自体の誤差については、以下のような定理が知られている。証明は それほど難しくないので、やってみること。
定理: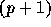 個の標本点
個の標本点 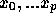 での、関数
での、関数 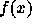 の値
の値 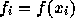 を標本値とする最小次数補間多項式
を標本値とする最小次数補間多項式 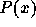 は以下の性質を持つ:
は以下の性質を持つ:
任意の xに対して、 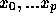 および x を含む最小の閉区間に
および x を含む最小の閉区間に
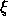 が存在し、
が存在し、
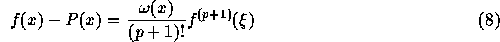
ここで、
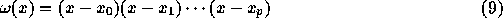
である。
ここで、 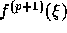 が問題の区間で一定であると思えば、誤差は
が問題の区間で一定であると思えば、誤差は
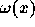 を積分したもので与えられる。
を積分したもので与えられる。
hでの等間隔補間の場合について、 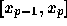 での積分誤差(陰的ア
ダムス公式の誤差)と
での積分誤差(陰的ア
ダムス公式の誤差)と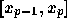 での誤差(陽的アダムス公式の誤差)
の係数を、いくつかの p の場合について下の表にまとめておく(実際の誤差
は
での誤差(陽的アダムス公式の誤差)
の係数を、いくつかの p の場合について下の表にまとめておく(実際の誤差
は 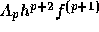 と書ける)。
と書ける)。
すぐにわかるように、陰的公式の誤差は圧倒的に小さい。このために、同じ刻 み幅であれば陰的公式のほうがそれだけ精度がいいことになる。
が、初期推定として陽的公式を使った場合、精度という観点からは、一回だけ
導関数を評価して直接代入したもの (Predict-Evaluate-Correct, PEC) 、あ
るいは反復をもう一回だけするもの [P(EC) ]で十分であり、完全に収束さ
せてもあまり意味がない。これは、精度の向上が、圧倒的とはいえせいぜい
1-2桁であるからである。
]で十分であり、完全に収束さ
せてもあまり意味がない。これは、精度の向上が、圧倒的とはいえせいぜい
1-2桁であるからである。
つまり、反復を繰り返しても、陰的公式の値に近付くが別に真の解には近付か ないのである。
さて、補間公式の構成について、まえに説明したのはラグランジュ補間の公式 をそのまま使う方法であった。これはこれで別にいけないわけではないのだが、 もう少しスマートな方法があるので、それを紹介しておく。
補間したい関数 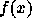 が、標本点
が、標本点 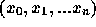 で、関数値
で、関数値
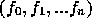 をとるとする。これを、以下のような形の多項式
をとるとする。これを、以下のような形の多項式
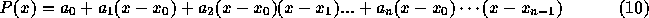
という形に書くことを考える。これを、 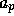 までをとったものは
までをとったものは 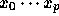 までを通る最低次補間多項式になっているように構成すること
にする。で、低い次数から順に作っていく。付け加える新しい項は、それまで
に使った点すべてで0になるので、新しい点で標本と一致するように
までを通る最低次補間多項式になっているように構成すること
にする。で、低い次数から順に作っていく。付け加える新しい項は、それまで
に使った点すべてで0になるので、新しい点で標本と一致するように 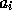 の
値を決めればいい。
の
値を決めればいい。
まず、n=0 については、 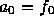 とすればいいのは明らかであろう。
次にn=1 であるが、
とすればいいのは明らかであろう。
次にn=1 であるが、
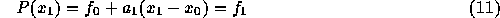
から

となる。同様に、 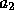 を求めると、
を求めると、

ただし、

である。
さて、段々式が繁雑になるが、もうちょっとの辛抱である。上の形は、

というふうにも書き直せることに注意しよう。これは、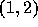 を通る補間式
の一次の係数と、
を通る補間式
の一次の係数と、 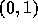 を通る補間式の係数の差みたいなものになっている。
を通る補間式の係数の差みたいなものになっている。
ここで、天下りに、 k 階差商 (divided difference) 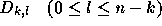 というものを導入する。これは以下のように定義される。
というものを導入する。これは以下のように定義される。
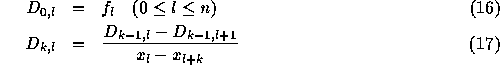
実は、このように定義された D が、

を満たす、求める係数であることを示すことが出来る。
証明には、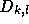 が、
が、 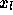 から始まる k+1点を通る補間多項式の係数
であるということを用いる。定義により
から始まる k+1点を通る補間多項式の係数
であるということを用いる。定義により

であるの。 ここで、帰納 法を使って証明することにすると、
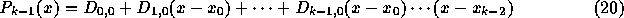
は、 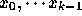 を通る k-1次補間多項式であり、また、
を通る k-1次補間多項式であり、また、
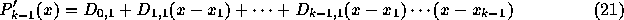
は、 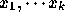 を通る k-1次補間多項式であるとしてよい。こ
の2つの線形結合によって、
を通る k-1次補間多項式であるとしてよい。こ
の2つの線形結合によって、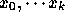 を通る補間多項式を作るに
は、
を通る補間多項式を作るに
は、
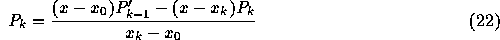
とすればよい。ここで、 と
と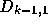 は、それぞれ
は、それぞれ 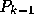 と
と
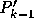 の最高次の係数であることに注意すると、
の最高次の係数であることに注意すると、 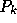 の最高次の係数(これは
の最高次の係数(これは 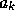 に等しい)
は、
に等しい)
は、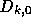 で与えられることがわかる。
で与えられることがわかる。
さて、
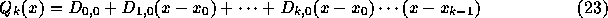
という多項式を考えると、これは 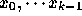 で
で 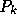 と一致し、
さらに最高次の係数も一致しているので、結局
と一致し、
さらに最高次の係数も一致しているので、結局 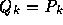 であることがわ
かる。つまり、
であることがわ
かる。つまり、 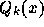 が求める補間多項式であり、
が求める補間多項式であり、 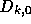 がその最高
次の係数ということになる。
がその最高
次の係数ということになる。
さて、なぜ上のような面倒な話をしたかというと、アダムス法において時間 刻みを変える方法の概念を説明するためである。
時間刻み一定であれば、すでに述べたようにあらかじめ係数を求めておいて、 前の関数値の線形結合で変化を計算できる。しかし、刻みを変えたい場合には そうはいかない。この時の、もっとも一般的で強力な方法は、上の差商を使っ て補間多項式を計算し、さらにそれを現在の時間刻みで積分した形の係数を求 める、すなわち、毎回積分公式を作り直すという方法である。差商の形でデー タをとっておくと、上の漸化式を使ってDを順番に更新することができる。 これは Krogh 型の公式と呼ばれ、かなり広い範囲の問題について、 もっ とも効率が良い公式であることがわかっている。(特別に高い精度を要求す る場合は、次回に述べる外挿法のほうがよいこともある)
上の方法で時間刻みを変えられるなら、出発公式は不必要になることに 注意しておく。つまり、最初は1次の予測子、2次の修正子から出発して、ステッ プ毎に次数をあげていけばいい。ステップサイズは次数を考慮して決めておく。
ステップを変えるのは上のような理由で大変だが、そのかわり誤差評価はルン ゲ・クッタに比べて容易である。予測子・修正子型の公式の場合、この2つの 間の差がかなり良い誤差の推定値(もちろん大きめだが)になっているので、 これを使ってやればいい。
必要な精度を決めた時、ほとんどどんな場合でも、線形多段階法のほうがルン ゲ・クッタ法よりも少ない計算量で答を得ることが出来るということが実験的 にも、また誤差の係数をつかった理論的な解析からもわかっている。
ルンゲ・クッタ公式が優れているのは、基本的にはその使いやすさにおいての みであるといってよい。が、まあ、使いやすさというのは実際的になかなか重 要であることも確かである。