まず、一変数の場合を考えよう。微分方程式の初期値問題
に対して、（前進）オイラー法とは以下のような方法である。
時刻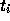 
での数値解が 
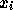であったとすると、時刻 
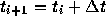での数値解を
という形に書く。
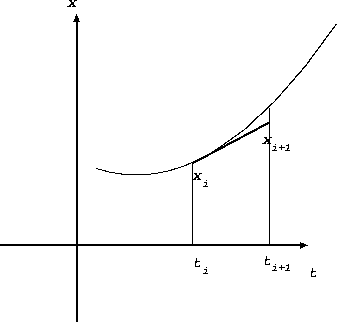
上の図に様子を示す。ここでは、真の解（がわかっているものとして）を曲線 で示し、そこから出発したとした。
やっていることはなんということはなくて、真の解に対する時刻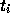 
での
接線を数値解ということにしようということである。
ある時刻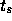 
での初期条件が与えられて、 
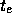での解を求めようという
時に、例えばその区間を n等分して
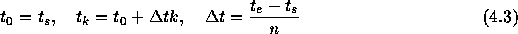
というふうに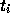 
を決めてやる。あとは 
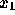から順に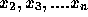 
と計算していけば、 
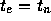での数値解
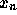が求まるわけ
である。
直観的には、 n を大きくしていけば、正しい答えに近付いていきそうな気 がするであろう。しかし、そうなるということをどうやって証明すればいいで あろうか？