


Next: References
Up: Astrophysics on the GRAPE
Previous: Black Hole Spiral-In
We will briefly discuss how the GRAPE computers have been used to
study the origin of structure in the Universe, from very small scales
to the largest scales that can be observed. On the small end, the
coagulation of grains and boulders to form planets has been modeled,
in order to understand the formation process of our own planetary
system, as well as that around nearby stars. Increasing the length
scale of interest by a factor of a billion, we discuss the formation
of galaxies. Multiplying the size by another factor of a thousand,
we reach the scale at which rich clusters of galaxies evolve.
After the Sun was formed, some matter of the proto-solar nebula was
left in a disk around the Sun. Grains that condensed out of the
original gas coagulated through collisions to form larger and larger
particles, the size of pebbles, boulders, and larger proto-planetary
bodies. To model this process in detail has turned out to be
difficult, because significant evolution takes place on a time scale
larger than a crossing time, by a factor of a million or more.
The main stumbling block has been the need to simultaneously model the
presence of a wide variety of particle sizes, or equivalently, masses.
A little more than ten years ago, it was realized that dynamical
friction plays an essential role in planetary
formation. [23,24] This process
forces more massive particles to have smaller random velocity, which
effectively increases their collision cross section. Thus, massive
particles can grow much more rapidly than less massive particles.
Kokubo and Ida [25] used the GRAPE-4 to model this type of growth of
planetesimals, under the assumptions that the accretion was perfect
( i.e. the collisions were totally inelastic) and that there was
no gas left in the system to cause non-gravitational drag on the
particles. They found the mass distribution to relax quickly to a
continuous power-law mass distribution with 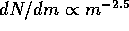 ,
where N is the cumulative number of bodies, independent of the
initial mass distribution (a result that was subsequently derived
analytically [26]). Their most interesting result was that
the heaviest body would subsequently detach from the continuous power
law distribution, featuring a much more rapid growth in mass, called
runaway growth, that could lead to the formation of a planet.
,
where N is the cumulative number of bodies, independent of the
initial mass distribution (a result that was subsequently derived
analytically [26]). Their most interesting result was that
the heaviest body would subsequently detach from the continuous power
law distribution, featuring a much more rapid growth in mass, called
runaway growth, that could lead to the formation of a planet.
Kokubo and Ida [27] again used the GRAPE-4 to study the later stages
of planet formation, on a more global scale. The earlier local
run-away studies, leading to the formation of a single protoplanet,
give rise to multiple protoplanet formation when a large fraction of
the protoplanetary disk is modeled. They found that such protoplanets
are formed and keep growing independently provided their orbital
separations are wide enough. After a while, the growth rate of these
protoplanets slows down, because their gravitational perturbations
increase the random motion of the swarm of planetesimals they are
embedded in. A continuous mass distribution of relatively light
planetesimals can thus coexists with a small number of large
protoplanets, for millions of years.
To study the formation of a single galaxy, it is important to model
its environment, out to large distances, given the long-range
character of the gravitational force, which through tidal effects
influences the angular momentum distribution within the contracting
gas clouds destined to form galaxies.
In addition, it is essential to model the gasdynamical effects that
influence the early phases of galaxy formation. While the
GRAPE has been designed primarily for stellar dynamical computations,
it has proved to be flexible in accommodating deviations
from an inverse square law. A key property of the GRAPE hardware
is that it uses the inter-particle distances, that are computed in
order to calculate the pair-wise gravitational forces, to construct
for each particle, a list of neighboring particles that reside within
a prescribed distance.
Using this neighbor list, hydrodynamical simulations can be run on the
front end workstation. The prime example here is smoothed particle
hydrodynamics, or SPH [28]. Examples of these types of
simulations include the formation of galaxies [29], the physical
origin of Ly-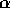 and metal line absorption systems [30], the
structure of galaxy clusters [31], and the fragmentation of molecular
clouds [32].
and metal line absorption systems [30], the
structure of galaxy clusters [31], and the fragmentation of molecular
clouds [32].
Simulations of galaxy formation have demonstrated that structure,
kinematics and chemical evolution of model galaxies which form in
hierarchical clustering scenarios agree with corresponding properties
of observed galaxy populations [33]. The major shortcoming is
that simulated galaxies are too concentrated. This is usually referred
to as the angular momentum problem [29] and suggests that
efficient feedback due to late stages of stellar evolution (for
example winds, and supernovae) is needed for a successful galaxy
formation model.
Simulations of damped Lyman-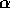 absorption systems demonstrated
that non-equilibrium dynamics can easily explain the apparent
discrepancy between the observed high velocity of low ionization lines
and the relatively small circular velocity predicted by hierarchical
models of structure formation. [30] The evidence that
damped Lyman-
absorption systems demonstrated
that non-equilibrium dynamics can easily explain the apparent
discrepancy between the observed high velocity of low ionization lines
and the relatively small circular velocity predicted by hierarchical
models of structure formation. [30] The evidence that
damped Lyman-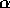 absorbers at high redshift are related to large
rapidly rotating disks, which would disagree with the hierarchical
clustering hypothesis, is thus not compelling. [34]
absorbers at high redshift are related to large
rapidly rotating disks, which would disagree with the hierarchical
clustering hypothesis, is thus not compelling. [34]
Galaxies are formed in a long drawn out process, starting somewhere
within the first billion years after the Big Bang, and continue to
form today. Most galaxies are formed in isolation or in small groups,
but some galaxies are form in much richer groups, called clusters of
galaxies, or even superclusters of galaxies. The typical properties
of galaxies formed in such clusters are different from galaxies
that were formed elsewhere. For example, most galaxies in clusters
are elliptical galaxies, whereas most field galaxies are spiral
galaxies. [35]
To what extent do these differences reflect the different formation
history of the galaxies, as they may have been affected by, for
example, the much higher matter density in the sites where rich
clusters of galaxies were born? And to what extent do the differences
reflect later modifications to the galaxies, as a result of the
different dynamical environment of a rich cluster? In attempts to
resolve this nature versus nurture debate, the GRAPE has been used to
model the internal evolution of a rich galaxy cluster.
Apart from the calculations by Bartelmann and Steinmetz [31],
already mentioned in the previous section, earlier work by
Funato et al. [36] simulated the evolution of clusters of
galaxies containing 32 to 128 galaxies. What they found is that `passive'
evolution of galaxies, caused by mutual encounters as well as by the
influence of the tidal field of the parent cluster, alters
the mass and size of individual galaxies. In particular, they
found that passive evolution leads to a distribution of masses with
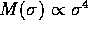 , where
, where 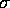 is the internal velocity
dispersion of the stars within a galaxy.
is the internal velocity
dispersion of the stars within a galaxy.
To understand the detailed mechanism of this passive evolution, Funato
and Makino [37] used the GRAPE-4 to study a large number of encounters
between two isolated galaxies, in order to determine how the resulting
changes of mass and binding energy depend on the models used for the
galaxies, and on the parameters describing the type of encounter.
They then estimated the cumulative effect of encounters, in the
setting of a rich cluster of galaxies. They again found that the mass
distribution of galaxies tends to approach 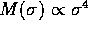 , for the mass M of a galaxy as a function of its velocity
dispersion
, for the mass M of a galaxy as a function of its velocity
dispersion 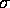 .
.
Their results resembles the
observational Faber--Jackson relation, the empirical result that the
luminosity of a galaxy 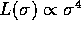 , for elliptical
galaxies. Note that the remnants of collisions between galaxies
typically resemble elliptical galaxies, even if the progenitors were
spiral galaxies or other types of galaxies. Because it is also
reasonable to assume that
, for elliptical
galaxies. Note that the remnants of collisions between galaxies
typically resemble elliptical galaxies, even if the progenitors were
spiral galaxies or other types of galaxies. Because it is also
reasonable to assume that 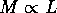 , this agreement with
observations suggests that the encounters of galaxies play an
important role in the evolution of galaxies in a cluster of galaxies.
, this agreement with
observations suggests that the encounters of galaxies play an
important role in the evolution of galaxies in a cluster of galaxies.



Next: References
Up: Astrophysics on the GRAPE
Previous: Black Hole Spiral-In
Jun Makino
Thu Nov 26 22:13:16 JST 1998
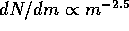 ,
where N is the cumulative number of bodies, independent of the
initial mass distribution (a result that was subsequently derived
analytically [26]). Their most interesting result was that
the heaviest body would subsequently detach from the continuous power
law distribution, featuring a much more rapid growth in mass, called
runaway growth, that could lead to the formation of a planet.
,
where N is the cumulative number of bodies, independent of the
initial mass distribution (a result that was subsequently derived
analytically [26]). Their most interesting result was that
the heaviest body would subsequently detach from the continuous power
law distribution, featuring a much more rapid growth in mass, called
runaway growth, that could lead to the formation of a planet.
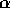 and metal line absorption systems [
and metal line absorption systems [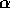 absorption systems demonstrated
that non-equilibrium dynamics can easily explain the apparent
discrepancy between the observed high velocity of low ionization lines
and the relatively small circular velocity predicted by hierarchical
models of structure formation. [
absorption systems demonstrated
that non-equilibrium dynamics can easily explain the apparent
discrepancy between the observed high velocity of low ionization lines
and the relatively small circular velocity predicted by hierarchical
models of structure formation. [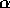 absorbers at high redshift are related to large
rapidly rotating disks, which would disagree with the hierarchical
clustering hypothesis, is thus not compelling. [
absorbers at high redshift are related to large
rapidly rotating disks, which would disagree with the hierarchical
clustering hypothesis, is thus not compelling. [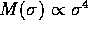 , where
, where 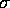 is the internal velocity
dispersion of the stars within a galaxy.
is the internal velocity
dispersion of the stars within a galaxy.
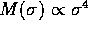 , for the mass M of a galaxy as a function of its velocity
dispersion
, for the mass M of a galaxy as a function of its velocity
dispersion 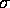 .
.
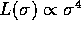 , for elliptical
galaxies. Note that the remnants of collisions between galaxies
typically resemble elliptical galaxies, even if the progenitors were
spiral galaxies or other types of galaxies. Because it is also
reasonable to assume that
, for elliptical
galaxies. Note that the remnants of collisions between galaxies
typically resemble elliptical galaxies, even if the progenitors were
spiral galaxies or other types of galaxies. Because it is also
reasonable to assume that 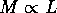 , this agreement with
observations suggests that the encounters of galaxies play an
important role in the evolution of galaxies in a cluster of galaxies.
, this agreement with
observations suggests that the encounters of galaxies play an
important role in the evolution of galaxies in a cluster of galaxies.