


Next: Acknowledgments
Up:
Thermal Relaxation in
Previous: 3 Results
In this paper, we studied the thermal relaxation process in
one-dimensional self-gravitating systems. We confirmed the result
obtained by Tsuchiya et al.[12] that the thermal
relaxation takes place in the timescale much longer than
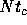 . However, we found that this is simply because the thermal
relaxation timescale is much longer than
. However, we found that this is simply because the thermal
relaxation timescale is much longer than 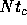 . Even for typical
sheets, the relaxation timescale is around
. Even for typical
sheets, the relaxation timescale is around 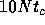 . In order to
obtain good statistics, we need to take average over many relaxation
times. Moreover, the relaxation time for sheets in the high-energy end
of the distribution function is even longer, since the relaxation
timescale grows exponentially as the energy grows. Thus, it is not
surprising that we have to wait for more than
. In order to
obtain good statistics, we need to take average over many relaxation
times. Moreover, the relaxation time for sheets in the high-energy end
of the distribution function is even longer, since the relaxation
timescale grows exponentially as the energy grows. Thus, it is not
surprising that we have to wait for more than 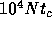 to obtain good
statistics.
to obtain good
statistics.
Does this finding have any theoretical/practical relevance?
Theoretically, there is nothing new in our result. What we found is
simply that numerical simulation should cover the period much longer
than the relaxation timescale to obtain statistical properties of the
system, and that the relaxation timescale of a sheet depends on its
energy. Both are obvious, but some of the previous studies neglected
one or both of the above, and claimed to have found a complex
behavior, which, in our view, is just a random walk.
Our finding of the long relaxation time by itself has rather little
astrophysical significance, since in the large N limit, the
relaxation time is infinite anyway. However, since any numerical
simulation suffers some form of numerical relaxation, it is rather
important to understand how the relaxation effect changes the
system. To illustrate this, we examine the claims by Tsuchiya et
al.[12] in some detail here.
They argued that the evolution of the mass sheet model proceeds in the
following four steps: (1) viliarization, (2) dynamical equilibrium,
(3) quasiequilibrium, and (4) thermal equilibrium. According to them,
the viliarization timescale is order of 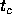 , and the energy of each
sheet is ``conserved'' in the dynamical equilibrium phase, which
continues up to
, and the energy of each
sheet is ``conserved'' in the dynamical equilibrium phase, which
continues up to 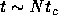 . Then, ``microscopic relaxation'' takes
place in the timescale of
. Then, ``microscopic relaxation'' takes
place in the timescale of 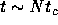 , where the energy of each
sheet is relaxed, but the whole system needs timescale much longer to
reach the true equilibrium, because of some complex structure in the
phase space.
, where the energy of each
sheet is relaxed, but the whole system needs timescale much longer to
reach the true equilibrium, because of some complex structure in the
phase space.
Our numerical results are in good agreement with those of Tsuchiya
et al.,[12] but our interpretation is much
simpler: First system virializes, and then relaxation proceeds in the
timescale of thermal relaxation, which depends on the energy of the
individual sheets. Thus, the central region with short relaxation time
relaxes to the distribution close to the thermal relaxation in less
than 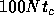 , but the distribution in the high-energy tail takes
much longer to settle. In addition, the small number statistics in the
high-energy region makes it necessary to average over many relaxation
times to obtain good statistics. In other words, there are no
distinction between the ``microscopic'' and ``macroscopic''
relaxation, and the evolution of the system is perfectly understood in
terms of the standard thermal relaxation.
, but the distribution in the high-energy tail takes
much longer to settle. In addition, the small number statistics in the
high-energy region makes it necessary to average over many relaxation
times to obtain good statistics. In other words, there are no
distinction between the ``microscopic'' and ``macroscopic''
relaxation, and the evolution of the system is perfectly understood in
terms of the standard thermal relaxation.



Next: Acknowledgments
Up:
Thermal Relaxation in
Previous: 3 Results
Jun Makino
Tue Mar 16 18:39:24 JST 1999
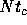 . However, we found that this is simply because the thermal
relaxation timescale is much longer than
. However, we found that this is simply because the thermal
relaxation timescale is much longer than 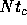 . Even for typical
sheets, the relaxation timescale is around
. Even for typical
sheets, the relaxation timescale is around 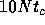 . In order to
obtain good statistics, we need to take average over many relaxation
times. Moreover, the relaxation time for sheets in the high-energy end
of the distribution function is even longer, since the relaxation
timescale grows exponentially as the energy grows. Thus, it is not
surprising that we have to wait for more than
. In order to
obtain good statistics, we need to take average over many relaxation
times. Moreover, the relaxation time for sheets in the high-energy end
of the distribution function is even longer, since the relaxation
timescale grows exponentially as the energy grows. Thus, it is not
surprising that we have to wait for more than 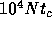 to obtain good
statistics.
to obtain good
statistics.
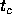 , and the energy of each
sheet is ``conserved'' in the dynamical equilibrium phase, which
continues up to
, and the energy of each
sheet is ``conserved'' in the dynamical equilibrium phase, which
continues up to 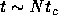 . Then, ``microscopic relaxation'' takes
place in the timescale of
. Then, ``microscopic relaxation'' takes
place in the timescale of 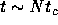 , where the energy of each
sheet is relaxed, but the whole system needs timescale much longer to
reach the true equilibrium, because of some complex structure in the
phase space.
, where the energy of each
sheet is relaxed, but the whole system needs timescale much longer to
reach the true equilibrium, because of some complex structure in the
phase space.
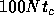 , but the distribution in the high-energy tail takes
much longer to settle. In addition, the small number statistics in the
high-energy region makes it necessary to average over many relaxation
times to obtain good statistics. In other words, there are no
distinction between the ``microscopic'' and ``macroscopic''
relaxation, and the evolution of the system is perfectly understood in
terms of the standard thermal relaxation.
, but the distribution in the high-energy tail takes
much longer to settle. In addition, the small number statistics in the
high-energy region makes it necessary to average over many relaxation
times to obtain good statistics. In other words, there are no
distinction between the ``microscopic'' and ``macroscopic''
relaxation, and the evolution of the system is perfectly understood in
terms of the standard thermal relaxation.