


Next: 2 境界値問題としてのLane-Emden 方程式
Up: 8 常微分方程式の数値解法:境界値問題
Previous: 8 常微分方程式の数値解法:境界値問題
Subsections
常微分方程式
![\begin{displaymath}
{{dy_i}\over{dx}} = f_i[x,y_j(x)]
\end{displaymath}](img332.png) |
(88) |
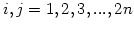 において、
において、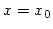 で
で
![\begin{displaymath}
g_k[y_j(x_0), x_0] = 0
\end{displaymath}](img334.png) |
(89) |
(但し、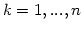 )、且つ
)、且つ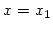 で
で
![\begin{displaymath}
g_l[y_j(x_1), x_1] = 0
\end{displaymath}](img337.png) |
(90) |
(但し、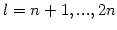 )を満たすよう解を求める場合を考えよう。
境界値問題という訳である。
例えば、初期値問題の例に挙げたのと同じ微分方程式
)を満たすよう解を求める場合を考えよう。
境界値問題という訳である。
例えば、初期値問題の例に挙げたのと同じ微分方程式
 |
(91) |
を、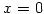 で
で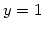 ,
, 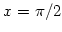 で
で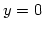 の下で解く境界値問題として考えよう。
の下で解く境界値問題として考えよう。
与えられた境界から、もう一方の境界に向かって初期値問題として積分する事を考える。
決められている条件は、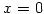 で
で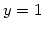 だけだから、初期値問題として積分を進めるた
めにはもう一つ条件を課す必要がある。そこで、
だけだから、初期値問題として積分を進めるた
めにはもう一つ条件を課す必要がある。そこで、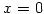 での
での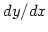 にある値を与えて
積分していくことにする。いろいろと、このパラメーターを変えてみて、もう一方の
境界での条件
にある値を与えて
積分していくことにする。いろいろと、このパラメーターを変えてみて、もう一方の
境界での条件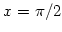 で
で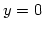 を満たすようなパラメーターを捜せば良い。
シューティング法という。
場合によっては、境界条件が特異になっていて、シューティング法ではなかなか当た
りが見つからない事がある。この様な場合は、それぞれの境界から、初期値問題とし
て他方の境界に向かって積分していき、ある適当な点(フィッティングポイント)で、
双方の解が接続するようにパラメーターを決める。これをフィッティング法と呼ぶ。
を満たすようなパラメーターを捜せば良い。
シューティング法という。
場合によっては、境界条件が特異になっていて、シューティング法ではなかなか当た
りが見つからない事がある。この様な場合は、それぞれの境界から、初期値問題とし
て他方の境界に向かって積分していき、ある適当な点(フィッティングポイント)で、
双方の解が接続するようにパラメーターを決める。これをフィッティング法と呼ぶ。
 |
(92) |
を、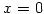 で
で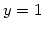 ,
, 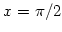 で
で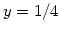 という境界条件の境界値問題として、
シューティング法により、数値的に解け。
という境界条件の境界値問題として、
シューティング法により、数値的に解け。
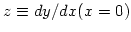 、
、
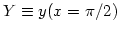 とすると、
この問題は
とすると、
この問題は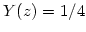 となる
となる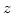 を求める
ことと同じである。
手順としては、
先ず、適当に選んだ
を求める
ことと同じである。
手順としては、
先ず、適当に選んだ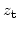 に対する
に対する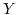 を
求める。
次に、
を
求める。
次に、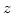 の値を
の値を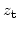 から
から
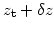 に変えて、
に変えて、
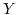 の変化量を求める。
これから
の変化量を求める。
これから
![\begin{displaymath}
dY/dz =
[Y(z_{\rm t}+\delta z)-Y(z_{\rm t})]/\delta z
\end{displaymath}](img350.png) |
(93) |
を数値的に求める。
今、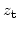 の値が、真の解
の値が、真の解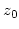 から
から
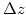 ずれているとすると、1次の精度で、
ずれているとすると、1次の精度で、
 |
(94) |
そこで、
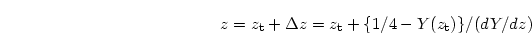 |
(95) |
を改めて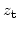 として、再び
として、再び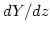 を計算し、
を計算し、
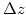 が充分小さくなるまで、逐次計算を繰り返せば良い。
が充分小さくなるまで、逐次計算を繰り返せば良い。
Jun Makino
平成15年4月17日
![]() で
で![]() だけだから、初期値問題として積分を進めるた
めにはもう一つ条件を課す必要がある。そこで、
だけだから、初期値問題として積分を進めるた
めにはもう一つ条件を課す必要がある。そこで、![]() での
での![]() にある値を与えて
積分していくことにする。いろいろと、このパラメーターを変えてみて、もう一方の
境界での条件
にある値を与えて
積分していくことにする。いろいろと、このパラメーターを変えてみて、もう一方の
境界での条件![]() で
で![]() を満たすようなパラメーターを捜せば良い。
シューティング法という。
場合によっては、境界条件が特異になっていて、シューティング法ではなかなか当た
りが見つからない事がある。この様な場合は、それぞれの境界から、初期値問題とし
て他方の境界に向かって積分していき、ある適当な点(フィッティングポイント)で、
双方の解が接続するようにパラメーターを決める。これをフィッティング法と呼ぶ。
を満たすようなパラメーターを捜せば良い。
シューティング法という。
場合によっては、境界条件が特異になっていて、シューティング法ではなかなか当た
りが見つからない事がある。この様な場合は、それぞれの境界から、初期値問題とし
て他方の境界に向かって積分していき、ある適当な点(フィッティングポイント)で、
双方の解が接続するようにパラメーターを決める。これをフィッティング法と呼ぶ。
![]() 、
、
![]() とすると、
この問題は
とすると、
この問題は![]() となる
となる![]() を求める
ことと同じである。
手順としては、
先ず、適当に選んだ
を求める
ことと同じである。
手順としては、
先ず、適当に選んだ![]() に対する
に対する![]() を
求める。
次に、
を
求める。
次に、![]() の値を
の値を![]() から
から
![]() に変えて、
に変えて、
![]() の変化量を求める。
これから
の変化量を求める。
これから