


Next: 3 恒星の固有振動
Up: 9 常微分方程式の数値解法:固有値問題
Previous: 1 フィッティング法
Subsections
Lane-Emden方程式(7.35)を固有値問題として解いてみよう。
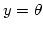 ,
,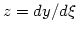 に対して、Lane-Emden 方程式は
に対して、Lane-Emden 方程式は
 |
(249) |
 |
(250) |
となる。境界条件は、
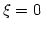 で
で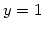 であり、どこか判っていない或る
であり、どこか判っていない或る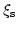 で
で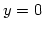 である。
この表面の値
である。
この表面の値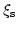 で
で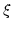 を規格化してやれば、
を規格化してやれば、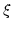 の範囲は
の範囲は![$[0,1]$](img664.png) となる。そこで、独立変数を
となる。そこで、独立変数を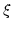 から
から
 |
(251) |
で定義する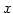 に変更すると、方程式は
に変更すると、方程式は
 |
(252) |
 |
(253) |
となり、境界条件は
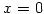 で
で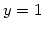 ,
,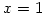 で
で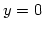 となる。
ここで
となる。
ここで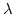 の値が幾つであるか、まだ判っていないが、この
の値が幾つであるか、まだ判っていないが、この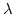 が
特別の値でしか、境界条件を満たせない。そこで、
が
特別の値でしか、境界条件を満たせない。そこで、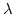 は固有値という事になる。
は固有値という事になる。
適当なフィッティングポイント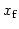 を設け、
中心からフィッティングポイントまでの解は前節で解説した通りの方法で求め、
その解に、表面、即ち
を設け、
中心からフィッティングポイントまでの解は前節で解説した通りの方法で求め、
その解に、表面、即ち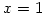 から
積分してきた解が、このフィッティングポイントで一致するようにすれば良い。
から
積分してきた解が、このフィッティングポイントで一致するようにすれば良い。
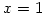 からの積分は、
からの積分は、
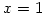 で
で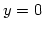 とし、そこでの
とし、そこでの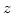 の値と
の値と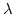 を与えれば出来る。
を与えれば出来る。
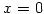 からの積分も
からの積分も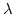 を与えれば出来る。
フィッティングポイントでの内側の解と外側の解との差は、従って、
を与えれば出来る。
フィッティングポイントでの内側の解と外側の解との差は、従って、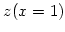 と
と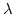 の関数と見做す事が出来る。未知数2つに対して、
の関数と見做す事が出来る。未知数2つに対して、
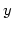 と
と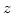 の内側の解と外側の解の差についての2本の式があるから、境界値問題として
Lane-Emden方程式を解いたのと同じ要領で、問題を解く事が出来る。
の内側の解と外側の解の差についての2本の式があるから、境界値問題として
Lane-Emden方程式を解いたのと同じ要領で、問題を解く事が出来る。
固有値問題として、Lane-Emden方程式を解け。
Jun Makino
平成15年4月17日
![]() を設け、
中心からフィッティングポイントまでの解は前節で解説した通りの方法で求め、
その解に、表面、即ち
を設け、
中心からフィッティングポイントまでの解は前節で解説した通りの方法で求め、
その解に、表面、即ち![]() から
積分してきた解が、このフィッティングポイントで一致するようにすれば良い。
から
積分してきた解が、このフィッティングポイントで一致するようにすれば良い。
![]() からの積分は、
からの積分は、
![]() で
で![]() とし、そこでの
とし、そこでの![]() の値と
の値と![]() を与えれば出来る。
を与えれば出来る。
![]() からの積分も
からの積分も![]() を与えれば出来る。
フィッティングポイントでの内側の解と外側の解との差は、従って、
を与えれば出来る。
フィッティングポイントでの内側の解と外側の解との差は、従って、![]() と
と![]() の関数と見做す事が出来る。未知数2つに対して、
の関数と見做す事が出来る。未知数2つに対して、
![]() と
と![]() の内側の解と外側の解の差についての2本の式があるから、境界値問題として
Lane-Emden方程式を解いたのと同じ要領で、問題を解く事が出来る。
の内側の解と外側の解の差についての2本の式があるから、境界値問題として
Lane-Emden方程式を解いたのと同じ要領で、問題を解く事が出来る。