上の線形化されたボルツマン方程式は、平衡解の回りならば何でも使えるが、
ここではもっとも簡単に解析できる場合として空間分布が一様な場合を考える。
これから ![]() は速度だけの関数であり、
は速度だけの関数であり、 ![]() は定数としていいことに
なるので
は定数としていいことに
なるので
| (20) |
| (21) | |||
| (22) |
| (23) |
| (24) |
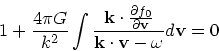 |
(25) |
もっとも、これはちょっと困った式で、
![]() が特
異点になっている。したがって、実数の振動数を考えるのはすこし厄介な話に
なる。まず、臨界点、すなわち振動数が
が特
異点になっている。したがって、実数の振動数を考えるのはすこし厄介な話に
なる。まず、臨界点、すなわち振動数が ![]() の場合と、不安定、すなわち振動
数が純虚数の場合を考えよう。
の場合と、不安定、すなわち振動
数が純虚数の場合を考えよう。