さて、この講義も回数ではすでにほぼ半分が終り、当初予定していた
のうちの最初の3つまでが済んだということになる。もっとも、それぞ れ大きなテーマであり、力学平衡モデルについては軸対称、あるいは3 軸不等なモデル、あるいはディスク系とその不安定モードなどについて は全く扱えていない。力学平衡への緩和過程についても、例 えば合体の場合、あるいは理想化された1次元系を例にとって具体的な 話をする必要もあったかもしれない。が、しかし、世の中は無衝突系だ けではないし、また、現実は無衝突系である場合でも、それを数値的に モデル化したものはそうでなくなってしまうことがある。従って、衝突 系の進化がどのようなものかということは、実際になんらかの自己重力 系を扱う場合には必ず理解しておく必要がある。というわけで、これか ら数回で衝突系の進化というものを考えることにする。
まず、2体緩和とはいったいどういうものかというところから話を始め ることにする。原理的には、これがなにかというのは結構厄介な問題で ある。
有限粒子数の自己重力多体系を考えると、これは以下のような進化をす ると考えられる。まず、最初は力学平衡になかったとすると、とりあえ ず力学平衡に落ちつく。粒子数が無限大であれば、無限に細かく見れば 無限に時間がたっても真の力学平衡に到達するわけではないが、まあ、 漸近はしていく。この時、各粒子は与えられたポテンシャルの中を運動 するだけになり、それ以上進化することはなくなる。
さて、実際には有限粒子数であるので、そもそも真の力学平衡というも のはない。有限の質量をもった各粒子が系の中を運動するに従って、ポ テンシャルは必ず変化するからである。この変化によって各粒子の軌道 も変化することになる。
それでは、粒子の軌道の変化を、粒子数が有限であることから来る成分 とそれ以外に分離することは可能であろうか?これは、系が力学平衡に あるとみなすことができればそれは可能である。つまり、力学平衡にあれ ば、粒子のエネルギー変化は定義によりすべて粒子数が有限であること によるからである。
が、良く考えると問題なのは、そもそも有限粒子数であるものを力学平 衡とみなすとはどういうことかということである。このあたりを考えて いると段々混乱してくるので、まず、理想化された状況から考えていく ことにしよう。
理想化といえば例によって一様等方な分布を仮定することである。例え ばマックスウェル分布があって、その中の一つの粒子をとって考えると いうことをしたいわけだが、これは結構厄介なのでさらに簡単な例を考 える。すなわち、速度0で空間内に一様(ランダム)に分布した質点を考 え、その中を質量0のテスト粒子を飛ばして見る。
もちろん、この場合エネルギー交換はないので速度は変わらず、単に散
乱されるだけだが、しかし、この例は2体緩和のいくつかの重要な性質
を示すのですこし詳しく見ていくことにする。分布している質点の質量
を ![]() 、数密度を
、数密度を ![]() とする。テスト粒子が一つの粒子から距離(イン
パクトパラメータ)
とする。テスト粒子が一つの粒子から距離(イン
パクトパラメータ) ![]() を速度
を速度 ![]() で通った時に曲がる角度は、実際に
ケプラー問題の解析解を使って
で通った時に曲がる角度は、実際に
ケプラー問題の解析解を使って
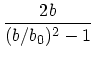 |
|||
| (10) |
さて、散乱の方向はランダムであると思われるので、平均としては(一
次の項は)0になる。しかし、 2次の項は0にならない。これは
| (11) |
この式から既にいろいろな性質がわかる。が、その前に理論的な困難を
解決しておく必要があるであろう。すなわち、この積分は
![]() で発散しているのである。これについてはいく
つかの考え方があった。例えば、初めて2体緩和の性質を理論的に調べ
た Chandrasekhar は、以下のように考えた。
で発散しているのである。これについてはいく
つかの考え方があった。例えば、初めて2体緩和の性質を理論的に調べ
た Chandrasekhar は、以下のように考えた。
「平均粒子間距離よりもインパクトパラメータが大きいような散乱は、 多体の干渉によって効かなくなるのでそこで積分を打ち切ってよい」
しかし、多体の干渉というようなものが実際にあるかどうかはあきらか ではない。もっと素直な解釈は、実際に系にあるすべての粒子と常に同 時に相互作用しているのだから、システムサイズくらいまで全部いれる (系が構造を持つ場合はちょっとややこしいが、密度の空間依存も積分 のなかに入れて全空間で積分する)というものである。
数値実験の結果などから、後者の解釈すなわち全体が効くというほうが 正しいということはかなり昔から大体わかっていた。歴史的には、どち らの解釈が正しいかについてはかなり最近まで論争があって、完全に決 着がついたといえるのは 94-5年頃である。が、これはまあそういうこと をいっている人もいたっていうくらいのもので、定説となっているのは 後者である。現在では後者の解釈が正しいということに疑いの余地はな い。
上の式から、適当に近似すると
| (12) |
さて、これからどんなことがわかるかというわけだが、これから、逆に
角度変化が1の程度になる時間というのを求めてみると、
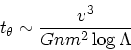 |
(13) |
今、![]() の質量依存性といったものを無視すると、散乱のタ
イムスケールは速度の3乗、数密度の逆数、質量の2乗の逆数に比例する
ということがわかったことになる。特に、質量密度一定の場合というも
のを考えてみると、タイムスケールが各粒子の質量に比例するというこ
とがわかる。
の質量依存性といったものを無視すると、散乱のタ
イムスケールは速度の3乗、数密度の逆数、質量の2乗の逆数に比例する
ということがわかったことになる。特に、質量密度一定の場合というも
のを考えてみると、タイムスケールが各粒子の質量に比例するというこ
とがわかる。
ある大きさを持った多体系というものを考えてみよう。質量![]() 、特徴的
な半径(ビリアル半径か何か)
、特徴的
な半径(ビリアル半径か何か) ![]() 、粒子数
、粒子数 ![]() とすれば、ビリアル定
理から
とすれば、ビリアル定
理から![]() 、力学的なタイムスケールが
、力学的なタイムスケールが
![]() となる。これを使うと上の緩和のタイムスケールは
となる。これを使うと上の緩和のタイムスケールは
| (14) |