例によって密度一様、速度分散がマックスウェル分布の恒星系で連星ができる 確率、というものを考えてみる。係数の細かいことは別にしてスケーリングだ けを考える。
これは、「2つの粒子が十分近くで相互作用している間にその近くにもうひとつがくる確 率」と考えられる。
質量 ![]() 速度分散
速度分散 ![]() 数密度
数密度 ![]() とする。
1つの粒子を考えると、十分近い距離というのは
とする。
1つの粒子を考えると、十分近い距離というのは ![]() なので
なので ![]() となり、散乱断面積は
となり、散乱断面積は
![]() である。従って、1つの粒子
がもうひとつと相互作用する確率は
である。従って、1つの粒子
がもうひとつと相互作用する確率は ![]() となる。相互作用している時間は
となる。相互作用している時間は
![]() であるので、相互作用している間にもうひとつと相互作用す
る確率は
であるので、相互作用している間にもうひとつと相互作用す
る確率は
ここでは散乱断面積とかに本当ははいってくる係数を全部無視して「1のオー ダー」としたが、 Goodman and Hut (1993) によれば最終的な結果の比例係数 は実際に 1 の程度であることが数値実験等によってわかっている。
恒星同士の2体の非弾性散乱によって本当に連星ができるのかどうかは本当の ところはよくわかっていない。もちろん、十分に近くを通れば2つは結合状態 になるし、その時に全角運動量を保存したままで円軌道の連星に進化するとす れば軌道長半径が最初の遭遇の時の近点距離よりちょっと大きいところ(計算 すること) で連星になる。
しかし、実際にそううまくいくかどうかは一部の質量が角運動量をもって逃げ ていくとか、星の内部の振動と軌道運動の間に共鳴が起こるかもしれないとか を考慮すると変わってくる。
大質量のブラックホールと普通の星、といった場合についてもこれは同様で、 連星になるケースが本当にあるのかどうかはわからない。
連星になるとすると、十分に近い距離、というのは基本的には単に星の半径の
程度になる。半径 ![]() が 90度散乱の距離
が 90度散乱の距離 ![]() に比べて十分小さい時には散乱断面積は
に比べて十分小さい時には散乱断面積は
![]() になり、形成確率は
になり、形成確率は
![]() の程度になる。
の程度になる。 ![]() なら連星にならないことに注意。
なら連星にならないことに注意。
単位時間当りのエネルギー変化は軌道長半径に依存しなくなる。このことをオー ダー見積もり程度の計算によって示してみる。
連星が他の星と相互作用してエネルギーを変えるためには、他の星が連星の軌道長半
径程度まで近づく必要がある。連星の軌道長半径を ![]() としよう。また連星
と周りの星の相対速度の典型的な値を
としよう。また連星
と周りの星の相対速度の典型的な値を ![]() とする。
とする。
まず、 連星の重力エネルギー ![]() は典型的な運動エネルギー
は典型的な運動エネルギー
![]() (係数適当)よりも大きいことに注意する。これは、近接遭遇する相手
が
(係数適当)よりも大きいことに注意する。これは、近接遭遇する相手
が ![]() 程度の距離まで連星に近づいた時には、 重力ポテンシャルによって速
度が大きくなっていることを意味する。言い換えると、角運動量保存のために、
無限遠方でのインパクトパラメータは
程度の距離まで連星に近づいた時には、 重力ポテンシャルによって速
度が大きくなっていることを意味する。言い換えると、角運動量保存のために、
無限遠方でのインパクトパラメータは ![]() よりずっと大きくなる。この効果
を gravitational focusing という。
よりずっと大きくなる。この効果
を gravitational focusing という。
この効果を一応式で計算してみる。連星と相手の合計の質量を ![]() とし、
無限遠でのインパクトパラメータを
とし、
無限遠でのインパクトパラメータを ![]() 、最も近付いた時の距離を
、最も近付いた時の距離を ![]() とす
る。また、この時の速度を
とす
る。また、この時の速度を ![]() とする
エネルギー保存から
とする
エネルギー保存から
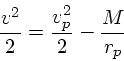 |
(2) |
角運動量保存から
| (3) |
これから少し整理すると
となる。連星の重力エネルギーが典型的な粒子の運動エネルギーより大きいこ
とから ![]() としてよいので、式 4 で右辺の最
初の項は無視できて
としてよいので、式 4 で右辺の最
初の項は無視できて
| (6) |
これは、結合エネルギー ![]() で考えると、散乱断面積が
で考えると、散乱断面積が ![]() に比例
する、ということに対応する。つまり、相互作用する典型的な時間間隔は
に比例
する、ということに対応する。つまり、相互作用する典型的な時間間隔は
![]() が大きくなるとそれに反比例して長くなる。
相互作用1回当りのエネルギー変化は
が大きくなるとそれに反比例して長くなる。
相互作用1回当りのエネルギー変化は![]() に比例するとしてよいので、
結局単位時間当りのエネルギー変化は一定となる。
に比例するとしてよいので、
結局単位時間当りのエネルギー変化は一定となる。
最終的には星団のポテンシャルからでていくか、合体で壊れる。
連星ともうひとつの星が相互作用すると、典型的には連星の結合エネルギーが 40% 程度大きくなる。その分のエネルギーは新しくできた連星の重心と、打ち 出された星の相対運動のエネルギーに変換される。
この時、連星が最初に十分ハードであれば、相互作用前にもっていた連星の重心と相 互作用の相手の運動エネルギーは相対的に小さくて、相互作用の後にもつエ ネルギーはエネルギー変化の分程度になる。星が全て等質量だとすると、 連星の重心の速度は打ち出される星の半分となる。単位質量当りでは 打ち出される星は連星の重心の 4 倍のエネルギーになる。
このような連星と単独星の相互作用が球状星団コアで起こると、初期の連星の
結合エネルギーが大きいとまず打ち出された星が、最終的には連星自体も星団
から打ち出されることになる。コアのポテンシャルの深さは![]() 単位で 10 か
ら 20 程度なので、連星は大体
単位で 10 か
ら 20 程度なので、連星は大体 ![]() 程度の結合エネルギーになると
星団に留まることができなくなる。
程度の結合エネルギーになると
星団に留まることができなくなる。
連星が等質量なら、 resonant interaction の結果どれが打ち出されるかは基 本的に等確率となる。
しかし、多少でも質量差があるとここは全く変わってくる。3体の resonant interaction の間にも、統計的には等分配になろうとするので、もっとも軽い ものが圧倒的に高い確率で打ち出されるからである。質量比が 2 倍程度もあ れば殆ど確実に最も軽いものがでていくことになる。
このため、連星と他の星の相互作用が無視できないような系では、連星になる のは選択的にもっとも重い粒子になる。星団の場合には、そのようなもっとも 重い星同士の連星が力学的摩擦のために速度を失って系の中心近くに居座るこ とになる。
ある程度ハードになると自分も相手も相互作用した後に星団コアから打ち出さ れるので、直接加熱になるかどうかは自明ではない。通常の理論モデルでは indirect heating といって、質量が失われる効果だけを考えればよい。
そうすると、結局、形成された連星が瞬間的にハードになってでていく、とい
うのが主な加熱機構になる。この時に、連星による星団コアの加熱率を大雑把
に求めてみよう。コアの質量が 1 で半径が 1 になるような単位系を使う。こ
のため、速度は1の程度になる。ま
た、粒子数を ![]() とする。すると、
式 1 から、単位時間にある星が連星になる確率は
とする。すると、
式 1 から、単位時間にある星が連星になる確率は
![]() になる。従って、単位質量当りの加熱率も
になる。従って、単位質量当りの加熱率も
![]() である。実際には、連星が与えるエネルギーはもうちょっと大きい
ので、
である。実際には、連星が与えるエネルギーはもうちょっと大きい
ので、![]() 程度になる。
程度になる。
さて、これを重力熱力学的崩壊の自己相似的収縮をしているコアから単位時間
に流れ出すエネルギーと比べると、これは緩和時間当り ![]() 程度である
ことが知られている。この2つが釣り合う辺りは
程度である
ことが知られている。この2つが釣り合う辺りは
現在のところ、星団内の連星の離心率の進化については殆どなにもわかってい ない。重力波による中性子連星の合体確率等を考えるには極めて重要であるが、 今後の研究課題である。
わかっていない理由は信頼できる数値計算をする方法がまだ存在しないことで ある。詳しくは次回くらいに。
これは、元々小惑星等について、軌道傾斜角の大きなものが木星の影響下でど のような振る舞いをするか、ということを調べた結果でてきたものである。 起こることは、軌道傾斜角と離心率がカップルして、非常に振幅の大きな振動 をすることがある、というものである。
これが起こる理由は、基本的には太陽と木星が作るポテンシャルを考えて、そ れの時間平均をとったものを考える(永年摂動を考える)と、木星が円運動と近 似すればポテンシャルは軸対称になり、全角運動量は保存しなくなる、という ものである。元のポテンシャルがケプラーに十分近いのでz軸周りの角運動量 以外にも保存量が残る。
連星についても、例えば回りにもうひとつ星があるとか、あるいは親星団のポ テンシャルがあるとかで内部運動のポテンシャルが球対称からずれることは一 般に起こる。そうなると、エネルギーは保存しても角運動量は保存しなくなる。
このような、時間定常な外場によって角運動量が保存しなくなる効果を一般に 古在機構と呼ぶこともある。
この効果は、摂動が小さくても変化の振幅が小さくならない(変化の速度は遅 くなるが)という著しい特徴があり、連星系の進化に対して極めて重要な役割 を色々なところで果たす。
木星の軌道が円軌道でないと、摂動ポテンシャルは軸対称でもなくなる。そう すると、2体問題でも摂動の結果軌道がカオスになる、といったことが起こる。 というわけで、次に少しだけカオスの話をする。