

次へ: 5 van Kampen mode
上へ: 天文学特別講義IV
戻る: 3 臨界点
次に、振動数が純虚数の場合を考えてみる。この時は、
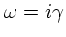 として元の式にマックスウェ
ル分布を入れて整理すると
として元の式にマックスウェ
ル分布を入れて整理すると
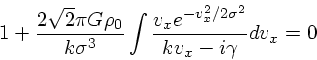 |
(31) |
ここで、被積分関数の分母を実数にするために
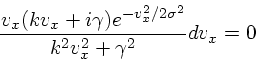 |
(32) |
と書き直すと、虚部は奇関数なので落ちる。実部は
![\begin{displaymath}
\int_0^{\infty} {x^2 e^{-x^2} \over x^2 + \beta^2} dx =
{ 1 ...
...rt{\pi} - {1 \over 2} \pi\beta
e^{\beta^2}[1-{\rm erf}(\beta)]
\end{displaymath}](img69.png) |
(33) |
なる関係を使って
![\begin{displaymath}
k^2 = k_J^2\left\{ 1- {\sqrt{\pi}\gamma \over \sqrt{2}k\sigm...
...rf}\left({\gamma
\over \sqrt{2}k\sigma}\right)\right]\right\}
\end{displaymath}](img70.png) |
(34) |
なんだかよくわからないが、まあ、 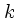 と
と 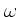 (
(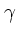 ) の関係を与
えてはいる。
) の関係を与
えてはいる。 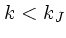 なら、ある実数
なら、ある実数 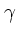 (正負どちらでも)があって
上を満たす。ただし、
(正負どちらでも)があって
上を満たす。ただし、 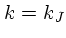 の場合と
の場合と 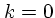 の極限を除いては、値は流体
の場合とは一致しない。
の極限を除いては、値は流体
の場合とは一致しない。
というわけで、波長がジーンズ波長よりも長いモードは流体と同様不安定で、
勝手に成長することになる。
Jun Makino
平成21年5月25日
![]() として元の式にマックスウェ
ル分布を入れて整理すると
として元の式にマックスウェ
ル分布を入れて整理すると
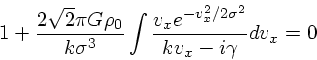
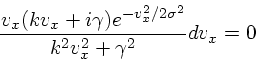
![\begin{displaymath}
\int_0^{\infty} {x^2 e^{-x^2} \over x^2 + \beta^2} dx =
{ 1 ...
...rt{\pi} - {1 \over 2} \pi\beta
e^{\beta^2}[1-{\rm erf}(\beta)]
\end{displaymath}](img69.png)
![\begin{displaymath}
k^2 = k_J^2\left\{ 1- {\sqrt{\pi}\gamma \over \sqrt{2}k\sigm...
...rf}\left({\gamma
\over \sqrt{2}k\sigma}\right)\right]\right\}
\end{displaymath}](img70.png)