

次へ: 6 Phase Mixing
上へ: 天文学特別講義IV
戻る: 4 不安定な場合
さて、それでは、音波に当たるような振動数が純実数のモードというものはあ
るのだろうか?これについては、 BT を含めて標準的な教科書でも若干混乱し
た記述がなされていることがある。以下、 van Kampen の論文 (1955,
Physica, 21, 949) に沿った理解を試みることにする。分散関係の一つ前の式
に戻ってみると、
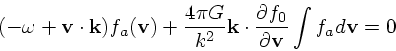 |
(35) |
となっている。面倒なのでまた 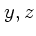 方向についてはあらかじめ積分すると、
方向についてはあらかじめ積分すると、
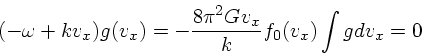 |
(36) |
ただし、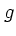 は
は 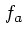 を
を 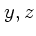 方向に積分したものである。また、
方向に積分したものである。また、 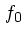 は
等方的であるとし、さらに
は
等方的であるとし、さらに
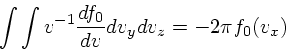 |
(37) |
なる関係を使った。これは、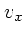 一定の平面上で極座標に変換すればすぐに
出てくる。上の式は
一定の平面上で極座標に変換すればすぐに
出てくる。上の式は 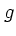 についての線形斉次な方程式で、
についての線形斉次な方程式で、
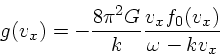 |
(38) |
という解を持つ。ここでは、
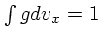 となるように規格化した。
ただし、意味のある解であるためには
となるように規格化した。
ただし、意味のある解であるためには
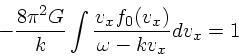 |
(39) |
を満たすようになっている必要がある。これは、最初に出した分散関係と実は
同じ式である。
最初にもいったように、この式がよろしくないのは 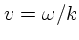 で積分が
特異になるからである。意味のある解を求める一つの考え方は、
で積分が
特異になるからである。意味のある解を求める一つの考え方は、 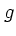 を超関数
に拡張してしまうことである:
を超関数
に拡張してしまうことである:
![\begin{displaymath}
g(v_x) = -{8 \pi^2 G v_x f_0(v_x)\over k}\left[{\cal P}{ 1\over \omega
- kv_x} + \lambda\delta(\omega - kv_x)\right]
\end{displaymath}](img83.png) |
(40) |
ここで 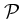 は主値をとるということで、要するに積分の不定性を
は主値をとるということで、要するに積分の不定性を
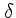 関数のほうに押しつけてみたというだけである。実際に、
規格化を満たすという条件から
関数のほうに押しつけてみたというだけである。実際に、
規格化を満たすという条件から 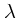 の値を決めることができる。この
「モード」は、任意の
の値を決めることができる。この
「モード」は、任意の 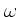 と
と 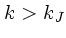 なる
なる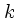 のすべての組合せに対し
て存在する。これを van Kampen mode という。
のすべての組合せに対し
て存在する。これを van Kampen mode という。
これがいったいどういうものかを少し考えてみよう。まず、 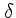 関数の
分は、
関数の
分は、
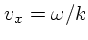 のところにだけ値があるということを示している。
つまり、位相速度が摂動を受けていないもともとの速度と等しい、いいかえれ
ば与えたものがそのままラグランジュ的に動いていくようなものである。これ
は、いま重力がまったくない極限を考えれば、単に摂動がまわりと相互作用す
ることなくそのまま動いていくというものであると考えられる。これにたいし
て、もう一つの項は重力による応答を示していると考えていい。
のところにだけ値があるということを示している。
つまり、位相速度が摂動を受けていないもともとの速度と等しい、いいかえれ
ば与えたものがそのままラグランジュ的に動いていくようなものである。これ
は、いま重力がまったくない極限を考えれば、単に摂動がまわりと相互作用す
ることなくそのまま動いていくというものであると考えられる。これにたいし
て、もう一つの項は重力による応答を示していると考えていい。
このへんはちょっとお話しになって申し訳ない(詳細を知りたいひとは van
Kampen の原論文に当たってほしい)が、 van Kampen モードは完備であるこ
とがわかっている。つまり、任意の摂動をvan Kampen mode の組合せとして表
現できる。
Jun Makino
平成21年5月25日
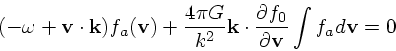
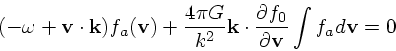
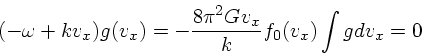
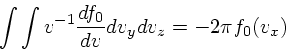
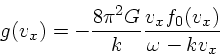
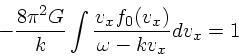
![]() で積分が
特異になるからである。意味のある解を求める一つの考え方は、
で積分が
特異になるからである。意味のある解を求める一つの考え方は、 ![]() を超関数
に拡張してしまうことである:
を超関数
に拡張してしまうことである:
![\begin{displaymath}
g(v_x) = -{8 \pi^2 G v_x f_0(v_x)\over k}\left[{\cal P}{ 1\over \omega
- kv_x} + \lambda\delta(\omega - kv_x)\right]
\end{displaymath}](img83.png)
![]() 関数の
分は、
関数の
分は、
![]() のところにだけ値があるということを示している。
つまり、位相速度が摂動を受けていないもともとの速度と等しい、いいかえれ
ば与えたものがそのままラグランジュ的に動いていくようなものである。これ
は、いま重力がまったくない極限を考えれば、単に摂動がまわりと相互作用す
ることなくそのまま動いていくというものであると考えられる。これにたいし
て、もう一つの項は重力による応答を示していると考えていい。
のところにだけ値があるということを示している。
つまり、位相速度が摂動を受けていないもともとの速度と等しい、いいかえれ
ば与えたものがそのままラグランジュ的に動いていくようなものである。これ
は、いま重力がまったくない極限を考えれば、単に摂動がまわりと相互作用す
ることなくそのまま動いていくというものであると考えられる。これにたいし
て、もう一つの項は重力による応答を示していると考えていい。