 |
以下が、今回のプログラムで使う木構造のためのクラス定義である。
pt minus 1 pt
#ifndef BHTREE_H
# define BHTREE_H
/*-----------------------------------------------------------------------------
* BHtree : basic class for C++ implementation of BH treecode
* J. Makino 2001/1/23
* Modified 2005/1/16
*-----------------------------------------------------------------------------
*/
#include "myvector.h"
#include "particle.h"
class bhnode
{
private:
myvector cpos;
real l;
bhnode * child[8];
particle * pfirst;
int nparticle;
myvector pos;
real mass;
public:
bhnode(){
cpos = 0.0;
l = 0.0;
for(int i = 0; i<8;i++)child[i] = NULL;
pfirst = NULL;
nparticle = 0;
pos = 0.0;
mass = 0.0;
}
};
#endif
BH というのがやたらでてくるが、これはこのアルゴリズムを1986 年に提唱したBarnes
と Hut (当時はどちらもプリンストン高等研究所。今は Barnes はハワイ大
学天文学科)の頭文字をとっているからである。 cpos は立方体の中心
座標、 l は辺の長さである。 child は子セル(ノード)へのポ
インタの配列であり、最大 8 個の子セルがあるので要素数 8 の配列にしてあ
る。これを使うことで、線形リストのように1つだけを指すのではなく、8個の
場所を指せるわけで、それによって木構造が表現できるわけである。
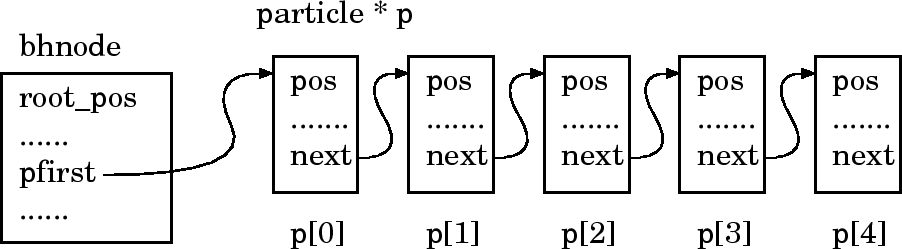
pfirst は中にある粒子のリストの先頭を指す。 nparticle はこ のリストの長さである。
ここで、ちょっと注意して欲しいのは、長さは本来必要ではないということで ある。つまり、リストを作る時に、最後の要素が NULL を指していると いうふうに決めたので、長さはリストをたどっていって数えればわかるわけで、 本来長さを別に覚えておく必要はない。が、数えなくても長さがわかると便利 なことが多いので別に覚えておくことにする。このようにした場合には、情報 が冗長になっているので2つの情報が矛盾しないように、あるいはちゃんと意 味があるほうを使うように注意する必要がある。
pt minus 1 pt
void bhnode::assign_root(myvector root_pos, real length, particle * p, int np)
{
pos = root_pos;
l = length;
pfirst = p;
nparticle = np;
for(int i=0;i<np-1;i++){
p->next = p+1;
p++;
}
p->next = NULL;
}
これはメンバ関数なので、bhnode クラス変数のメンバはメンバ名だけ
で使える。中心座標、辺の長さと、粒子の配列、粒子数が引数で渡ってくるの
で、中心座標、辺の長さをメンバ変数に代入し、 pfirst から始まるリ
ストを配列の要素を順にたどっていくように作っておく。
これは、元々の粒子の配列の順番にリストを作っただけで、この段階では意味 がないように見える。何故わざわざこういうことをするかは次に木構造を作る ところでわかる(と思う)。
次に実際に木構造を作っていく。これは、以下のようになる
pt minus 1 pt
void bhnode::create_tree_recursive(bhnode * & heap_top, int & heap_remainder)
{
for(int i = 0;i<8;i++)child[i] = NULL;
particle * p = pfirst;
for(int i=0 ; i<nparticle; i++){
particle * pnext= p->next;
int subindex = childindex(p->pos,cpos);
assign_child(subindex, heap_top, heap_remainder);
child[subindex]->nparticle ++;
p->next = child[subindex]->pfirst;
child[subindex]->pfirst = p;
p=pnext;
}
for(int i=0; i<8;i++) if(child[i]!=NULL){
if (child[i]->nparticle > 1){
child[i]->create_tree_recursive(heap_top, heap_remainder);
}else{
child[i]->pos = child[i]->pfirst->pos;
child[i]->mass = child[i]->pfirst->mass;
}
}
}
ここで、渡ってきている引数は、実際には bhnode 構造体の配列の先頭アド
レスと、その配列の要素数、というか正確にはその配列のどこか途中のアドレ
スと残りの要素数である。この配列は、木構造全部を作るのに十分な程度の大
きさをとっておく。木に新しいノードを付け加えるためには配列の先頭から順
番に要素を割り当てていく。
一般には、木構造のような動的な構造を作るには、 new 演算子を使っ て必要に応じて新しいメモリ領域を割り当てる。が、ここでは木構造は時間積分 のステップ毎に新しく作るので、 new をその度に使ってはメモリが足 りなくなるとかややこしい問題がある。そこで、自前でメモリを配列に確保してお いてそこにあるものを使うことにする。足りなくなったらここではエラーを出 して終る。
まず、最初にすることは、自分の下にある全粒子をたどっていって、それがど の子ノードにいくかを判定し、結果に応じて対応するリストに挿入(先頭に追 加)することである。ここで、 next は自分のリストなので、これを書 き変えるとその後がたどれなくなる。このため、ループの最初に自分の次とい うのを pnext に憶えておく。判定は、各座標方向に対して、中心より上 か下かを見るだけである。これは、以下の関数が行う。
pt minus 1 pt
int childindex(myvector pos, myvector cpos)
{
int subindex=0;
for(int k=0;k<3;k++){
subindex <<= 1;
if (pos[k] > cpos[k])subindex += 1;
}
return subindex;
}
どの子ノードに入るかが決まったら、実際に子ノードに入れる。その前に、そ の子ノードに bhnode を割り当てたかどうかをチェックし、既に割り当 ててなかったら新しく割り当てる。これは以下の関数である。
pt minus 1 pt
void bhnode::assign_child(int subindex,
bhnode * & heap_top,
int & heap_remainder)
{
if (heap_remainder <= 0){
cerr << "create_tree: no more free node... exit\n";
exit(1);
}
if (child[subindex]==NULL){
child[subindex] = heap_top;
heap_top ++;
heap_remainder -- ;
child[subindex]->cpos = cpos + myvector( ((subindex&4)*0.5-1)*l/4,
((subindex&2) -1)*l/4,
((subindex&1)*2 -1)*l/4);
child[subindex]->l = l*0.5;
child[subindex]->nparticle=0;
}
}
ここでは、座標の計算とかもついでにしているので少し長い関数になっている。
実際の粒子の割り当ては、
pt minus 1 pt
child[subindex]->nparticle ++;
p->next = child[subindex]->pfirst;
child[subindex]->pfirst = p;
の部分である。子ノードの粒子の数を憶えておく nparticle を1増やし、 child[subindex]->pfirst を p にすればいいわけだが、そうす るとこれまでchild[subindex]->pfirst が指していたものがどこかにいっ てしまうので、その前に child[subindex]->pfirst を p->next に代入しておく。
全部の粒子の子ノードへの振り分けがすんだら、 粒子が2つ以上入っている子ノードをさらに分割する。これは、 ここではこの関数自身を再帰的に呼び出すことで実現されている。粒子が1つ だけなら、その質量、位置を木構造データのほうの変数にコピーしておく。
ここで、再帰的な関数が、「自分のリストを見て子供のリストを作る」という 形になっているので、最初にルートノードに対してリストを作る必要があった ことがわかる。
と、今日はとりあえずこれくらいで。来週はこれを使った重力の計算をしてみ る。