| (8) |
もう一回式を書いておく。
| (8) |
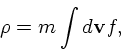 |
(10) |
なお、以下の議論では(当分) ![]() のことは忘れて、その代わり
のことは忘れて、その代わり ![]() が個数
密度ではなくて質量分布であるということにしておく。
が個数
密度ではなくて質量分布であるということにしておく。
今日は、これらから、まず、「力学平衡状態」とはどう定義され、どういう性 質があるかということを考え、それから具体的な平衡状態の例を見ていくこと にする。
まず、「力学平衡」とは何かということだが、これは、上の無衝突ボルツマン
方程式とポアソン方程式を連立させたものの定常解、すなわち、時間的に変化
しない解ということになる。従って、ある分布関数 ![]() が力学平衡にあると
いうことは、それによって決まるポテンシャル
が力学平衡にあると
いうことは、それによって決まるポテンシャル ![]() を固定して考えた時に、
を固定して考えた時に、
![]() の時間微分が
の時間微分が ![]() になるということである。
になるということである。
ここで、わざわざ「力学」とつけるのは、もちろん平衡状態にはほかにもいろ いろあるからである。もっとも重要なのは熱平衡の概念であるが、これはまた 後で。