ここまでは、等温モデルの変形で、有限質量としたキングモデルと、それ から多成分系の例として球対称等温な恒星系の中での等温ガスの分布を扱った。 以下では、非等方モデルの簡単な例をあげ、それからモデルを離れて恒星系の平 衡状態の一般的な性質について考える。
非等方ということは、分布関数が ![]() の形で書けるということである。
まず、密度
の形で書けるということである。
まず、密度 ![]() がどう書けるかを考えてみよう。一般の分布関数で、密度
は単に
がどう書けるかを考えてみよう。一般の分布関数で、密度
は単に ![]() を速度空間全体で積分したもの
を速度空間全体で積分したもの
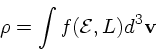 |
(31) |
| (32) |
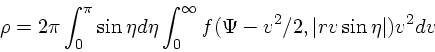 |
(33) |
一般に ![]() が
が ![]() に依存するしかたというのは無限にあるわけだが、以下、
そのなかで割と扱いやすいものとして、分布関数が
に依存するしかたというのは無限にあるわけだが、以下、
そのなかで割と扱いやすいものとして、分布関数が
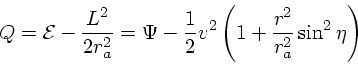 |
(34) |
![\begin{displaymath}
\rho = 2\pi \int_0^{\pi}\sin \eta d\eta \int_0^{\Psi}f(Q)
{ \sqrt{2(\Psi - Q)} \over [1 + (r/r_a)^2\sin^2\eta]^{3/2}}dQ
\end{displaymath}](img85.png) |
(35) |
![\begin{displaymath}
\int_0^{\pi}{\sin \eta d\eta \over [1 + (r/r_a)^2\sin^2\eta]^{3/2}}
= {2 \over 1 + (r/r_a)^2}
\end{displaymath}](img88.png) |
(36) |
非等方分布などを実際に、例えば観測データの説明として使うためには、与え
られた密度に対して、それを実現するような分布関数を作るという作業が必要
になる。これを、まず ![]() の場合についてやってみて、Osipkov-Merritt
モデルの場合にも応用してみる。
の場合についてやってみて、Osipkov-Merritt
モデルの場合にも応用してみる。
式 38 で、密度が至るところ正ならば ![]() は
は ![]() の単調な
関数なので、
の単調な
関数なので、 ![]() を
を ![]() の関数と思って、両辺を
の関数と思って、両辺を ![]() で微分すれば
で微分すれば
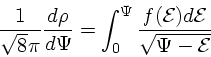 |
(39) |
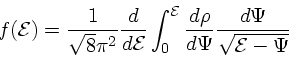 |
(40) |
例として、Jaffe model
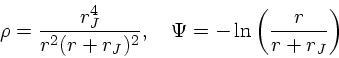 |
(42) |
| (43) |
![\begin{displaymath}
f(E) = {M \over 2\pi^3(GMr_J){3/2}}\left[F_-(\sqrt{2{\cal E}...
...- \sqrt{2} F_+(\sqrt{{\cal E}})
+ F_+(\sqrt{2{\cal E}})\right]
\end{displaymath}](img99.png) |
(44) |
但し、
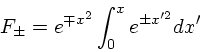 |
(45) |
さて、ちょっと疲れて来たかも知れないが、式37と式
38が左辺に ![]() がつく以外は同じ形をしてい
たということを思い出して欲しい。式41は式
38の解であったわけなので、今
がつく以外は同じ形をしてい
たということを思い出して欲しい。式41は式
38の解であったわけなので、今
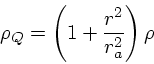 |
(46) |
最後に、Osipkov-Merritt モデルの性質について少し考えてみる。分布関数が
![]() によるという
ことは、
によるという
ことは、![]() の等高線が放物線になっているということである。中心近く
では、どうぜ
の等高線が放物線になっているということである。中心近く
では、どうぜ ![]() の取り得る値の範囲が狭いので、実は等方的な場合とあま
り変わらない。これに対し、外側の
の取り得る値の範囲が狭いので、実は等方的な場合とあま
り変わらない。これに対し、外側の ![]() に近いところでは、等方の場合から
大きくずれる。
に近いところでは、等方の場合から
大きくずれる。
ずれ方は、通常の ![]() は
は![]() の減少関数なので、
の減少関数なので、 ![]() についてもそうなり、
外側にいくほどcircular に近い軌道が減り、radial に近い軌道を持つ粒子が
相対的に増えることになる。
についてもそうなり、
外側にいくほどcircular に近い軌道が減り、radial に近い軌道を持つ粒子が
相対的に増えることになる。
このような傾向は、例えば楕円銀河などの形成過程についてのいろいろなシナ リオで自然に起きること(そのうちに扱う)であり、理論的に調べられている 非等方モデルは大抵上のような角運動量でカットオフを持つようなモデルになっ ている。
なお、非等方性の重要な観測的応用として、楕円銀河の中心部の構造のモデル があるが、これについては後で時間があれば触れることにしたい。