

次へ: 4 不安定な場合
上へ: 天文学特別講義IV
戻る: 2 恒星系でのジーンズ不安定とランダウ減衰
式が繁雑なので、いま、
波数ベクトルを 軸方向にとることにすると、分散
関係は
軸方向にとることにすると、分散
関係は
 |
(26) |
臨界安定で  とすれば、結局
とすれば、結局
 |
(27) |
となる。 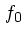 が
が  で有限で微分可能なら積分は求まるので、これか
ら
で有限で微分可能なら積分は求まるので、これか
ら  となる波数
となる波数  は決まる。
は決まる。
流体の場合と対応をつけるために、速度分布 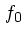 をマックスウェル分布
をマックスウェル分布
 |
(28) |
にしてみる。
これは例によって
 |
(29) |
を使って全部積分できて、
 |
(30) |
となる。これは、流体の場合と同じになっている。つまり、中立安定な波長
(ジーンズ波長)は、恒星系と流体で同じである。
Jun Makino
平成21年5月25日
![]() 軸方向にとることにすると、分散
関係は
軸方向にとることにすると、分散
関係は


![]() をマックスウェル分布
をマックスウェル分布

