
さて、まず対称型公式とはなにかということだが、まず時間反転に対する対称性というものを定義しておこう。時間反 転に対する対称性とは、常微分方程式

に対する一段法

が、

を満たすこと、つまり、直観的には、ある微分方程式系があって、それを1ス テップ分数値解を求めたとする。で、そこから逆に戻ると厳密に元の値に戻る ということである。(ここでは丸め誤差はないものとする)
で、一段法の場合には、この意味で対称なものを対称型公式ということにする。
具体例で考えてみよう。例えば前進オイラー法は対称型ではない。これは、いっ た先で導関数を計算すれば、一般にもとのところでの導関数とは違うから当然 であろう。前進オイラー法が対称ではないのだから、その逆写像である後退オ イラー法も対称型ではないことになる。
では、対称型にはどういうものがあるかということだが、明らかに対称型であ るものとしては、台形公式

がある。これが上の対称性を満たしていることはいうまでもない。
さて、なぜこの型の公式を考えるかということであるが、これは実はそれほど 簡単な話ではない。実験的には以下のようなことが知られている。
前のほうの性質はシンプレクティック公式と同じであるが、後の方の性質はシ ンプレクティック公式よりもある意味でよいものである。
理論的な話は来週に回して、今日はとりあえず対称型公式にはどんなものがあ るかという話をしておこう。
さて、一階の方程式に対する一段法という制限をつけた場合、つまり、ルンゲ クッタ法の場合、対称な公式はかならず陰的公式になる。逆に、陰的公式であ れば対称型のものを作るのは容易である。つまり、ルンゲクッタ法を与える行 列 A とかベクトル b, cが対称になっていればいい。
何度もでてきたので予想されるかもしれないが、陰的ガウス法は対称型公式で もある。
一階の系に対する一段法では、そういうわけですでに紹介してきた陰的 RK の ほかにうまい方法があるわけではない。それでは、
以下、順番に考えていくことにする。
実は、前回にすでに述べたように、 leapfrog 公式は対称型でありしかも陽公 式である。で、前回紹介した leapfrog の組合わせで作られる公式も、実は すべて対称型になっている。
さて、一段法という枠を外してみよう。2階の方程式用の線形多段階法として は、すでに Stormer-Cowell 法について述べた。が、これは対称型ではない。
というようなことをいう前に、線形多段階法に対する対称性の定義を与える必 要がある。ここでは、以下のように定義しておこう。 2階の方程式用の線形多段階法は、一般に
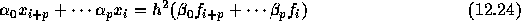
という形に書くことができる。 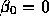 なら陽的であるし、そうでな
ければ陰的公式である。ここで、対称型であるとは、係数が
なら陽的であるし、そうでな
ければ陰的公式である。ここで、対称型であるとは、係数が

を満たすということである。 leap frog をこの形にしたものは、 前に出てき た通り

というものであり、これが上の対称性の定義を満たしていることはいうまでも ないであろう。
上の意味で対称な公式は、実際に時間反転に対して対称であるということに注
意しておこう。つまり、 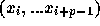 から上の式で
から上の式で 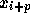 を求めたとする。時間を逆転させた解を考えて、
を求めたとする。時間を逆転させた解を考えて、
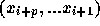 から
から 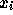 を求めるということを考えても、使
う式が時間が逆転していないものと同じになっているのである。
を求めるということを考えても、使
う式が時間が逆転していないものと同じになっているのである。
Stormer-Cowell が対称ではないというのはこの意味、つまり、
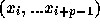 から
から 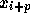 を求める式と
を求める式と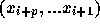 から
から 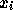 を求める式が同じもの
ではないということである。
を求める式が同じもの
ではないということである。
このような公式は、 1970 年代から知られていたが、注目されるようになった のは 1990 年代に入ってからである。特にトロント大の Quinlan, Tremaine らが14次までの対称型公式を導いた。表12.1にその値を示してお く。
なお、非常に最近(今年)になって、国立天文台の福島によって、Quinlan & Tremaine によるものよりもはるかに良い性質を持つものが導かれている。こ れについては原理も合わせて後で触れる。
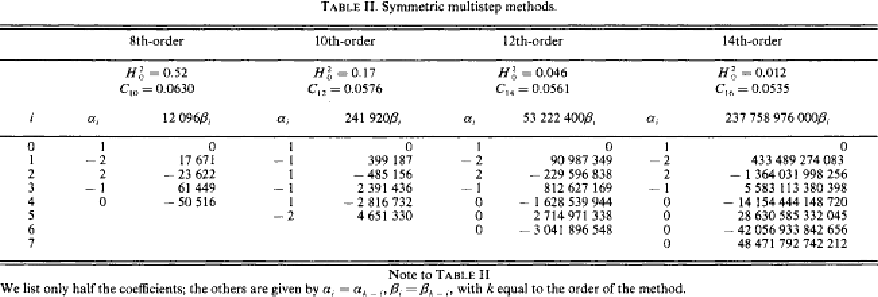
表 12.1: Quinlan & Tremaine 1990 による対称型公式の係数
一般に対称型というわけではないが、4次の対称型公式を導く特別な方法とし てエルミート型(あるいはエルミート・オブレヒホフ型)と呼ばれる公式のク ラスについてここで触れておこう。
エルミート型公式は、線形多段階法のアダムス型公式の一つの一般化である。 どのような意味において一般化であるかというと、アダムス型と同じように補 間多項式を積分することで新しい時刻での値を求めるところは同じである。違 うところは、アダムス型公式では補間多項式を作るのに関数の値を使う(ラグ ランジュ・ニュートン補間)が、エルミート型公式では、関数の導関数の値も 使うのである(エルミート補間)。
もっとも単純な発想としては、テイラー法というものがある。つまり、微分方 程式

というものがあったとしたら、

という関係式を使って fの全微分を求めることが出来、同様に高次の導関数 もどんどん計算していくことが出来る(微分が式で書ければ)。これらを使っ て直接テイラー級数を評価して近似解を求めるのである。
高次の導関数が簡単に求められる場合(例えば線形な系とか)には、この方法 はかなり強力である。線形多段階法やルンゲクッタに比べて誤差項の係数がずっ と小さく、タイムステップが大きくとれるからである。
が、多くの問題において、高階導関数の直接計算は現実的ではない。これは、 計算量が指数関数的に爆発するのが普通だからである。とはいえ、fの一階 導関数や二階導関数くらいならば指数関数的といってもたかがしれている。し かしながら、これではテイラー法では2次や3次の公式しか作れない。実用的な 公式としては、(leap frog のような特別に良い性質をもっているとかいうの でなければ)もうちょっと高次のものが必要である。
そこで考えられるのが、高階導関数を使ってさらにルンゲ・クッタ型とか線形
多段階法のような公式を作ることである。例によってもっとも簡単な場合とい
うのを考えると、それは 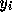 と
と  のところで f の一階導関数
の値を使うもの(高次導関数を使わないものであれば台形公式に相当)の一般
化ということになろう。
のところで f の一階導関数
の値を使うもの(高次導関数を使わないものであれば台形公式に相当)の一般
化ということになろう。
台形公式は、2次の陰的アダムス型公式と考えることができる。つまり、 f を線
形補間してそれを積分しているわけである。これに対し、 f と 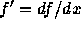 を使う補間というのはどういうものかということを考えてみると、こ
れは 3次多項式を構成できることがわかる。具体的には、導関数の近似多項式
を
を使う補間というのはどういうものかということを考えてみると、こ
れは 3次多項式を構成できることがわかる。具体的には、導関数の近似多項式
を
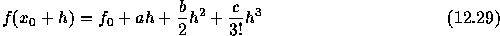
としたとき、
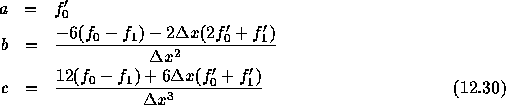
という形で係数を求めることが出来る。さらに、上の近似多項式を積分してや れば、結局
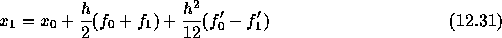
という形の公式が得られる。これは台形公式と同じく陰的公式である。対称型 であることは明らかであろう。
この公式は実装が簡単であるわりには精度が高く、また対称型であるというよ い性質をもつこともあり、良く使われるようになりつつあるようである。収束 させるための反復には普通の逐次代入が使える。
対称型一段公式には、対称性を保ったままで時間刻みを変更できるというシン プレクティック公式では(普通の意味では)なかった良い性質がある。以下で は、どのようにしてそれが可能であるかを簡単に述べておく。
今、任意の対称型一段法があって、その時間刻みを与える関数として 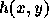 が与えられているとする。ここで
が与えられているとする。ここで 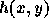 はなんでもいいが、これも一段法
である、つまり前のステップの値とかを必要としないものであるとする。
はなんでもいいが、これも一段法
である、つまり前のステップの値とかを必要としないものであるとする。
一般に、 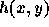 によって刻み幅を決めて求めていった数値解は、時間反転
に対する対称性を満たしていない。つまり、1ステップ積分してから、逆に戻
すと、タイムステップが変わってしまうためにもとのところに戻らない。この
ことのために、例えば周期軌道の場合に誤差が周期的にならないということが
起こるわけである。
によって刻み幅を決めて求めていった数値解は、時間反転
に対する対称性を満たしていない。つまり、1ステップ積分してから、逆に戻
すと、タイムステップが変わってしまうためにもとのところに戻らない。この
ことのために、例えば周期軌道の場合に誤差が周期的にならないということが
起こるわけである。
刻み幅を変えつつ時間反転に対する対称性を保つ一つの方法は(これ以外の方
法もあるかもしれないが、今のところ知られていない)、 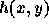 自体に対
称性を持たせることである。つまり、一段法を
自体に対
称性を持たせることである。つまり、一段法を

という形に書いた時、

がなりたつことを保証するように h を決めるのである。具体的には、上の 対称性が成り立っていないような時間刻みの式 h があった時に、

によって対称化した時間刻みを作ればいいことになる。この場合時間刻み自体 が陰的に決まることになるが、とにかく対称性という要求は満たされるのであ る。
さて、時間刻みの変更にはもう一つ全く違ったアプローチがある。 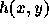 が時間刻みを与える関数であるとすると、新しい独立変数 s を
が時間刻みを与える関数であるとすると、新しい独立変数 s を

によって導入し、元の微分方程式

を s を独立変数として書き直す。 x はいまや従属変数なので、方程式

を積分して求める必要があるが、この変換された方程式はs の刻み幅一定で解け ることになる。この場合には時間刻みを陰的に決める必要はない。
が、この方法を使った場合、リープフロッグのような陽的方法は多くの場合に 使えない。これは、変換したあとの系はハミルトン系になるという保証はない し、そうなるように変換を選んだとしてもハミル トニアンがリープフロッグが使える特別な形( p と q が分離しているも の)になるとは限らないからである。
さらに、元の方程式を書き直す必要があるので、プログラムを書くのは結構大 変な作業になることが多いということも、この方法の問題点ではある。
というわけで、前の時間刻みを陰的に変える方法とどちらがいいかは時と場合
による。時間刻みの関数 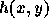 が簡単なもので良ければ、方程式の書換え
も単純でありこっちの方法の方が良い結果が得られる。が、 hが簡単ではな
い場合(例えば、埋め込み型RK公式から誤差推定が得られ、それを一定値に保つよ
うに刻みを決める)には、前節で述べた方法を使うしかない。
が簡単なもので良ければ、方程式の書換え
も単純でありこっちの方法の方が良い結果が得られる。が、 hが簡単ではな
い場合(例えば、埋め込み型RK公式から誤差推定が得られ、それを一定値に保つよ
うに刻みを決める)には、前節で述べた方法を使うしかない。