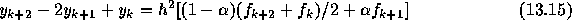
に対して、
- Interval of Periodicity を求めよ
- 次数を求めよ。 2 より高くなることはあるか?

- 等時間刻みの 4次シンプレクティック法(例えば吉田の方法)を使って時間積
分することを試みよ。安定な解を得るためにはステップサイズがどの程度であ
る必要があるか?なお、計算例としては例えば
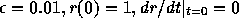 としてみよ。
としてみよ。
- 適当な方法で可変時間刻みにして、精度と計算量(ステップ数)の関係 を等時間刻みの場合と比較せよ。

は特別な初期条件を除いては安定な軌道を持たない。数個の粒子の場合につい て適当な初期条件からいろいろな方法で数値積分し、しばらく計算した後での 答を比較してみよ。さらに、結果が「正しい」ということができるのはどうい う場合かを考察せよ。