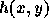対称型一段公式には、対称性を保ったままで時間刻みを変更できるというシン プレクティック公式では（普通の意味では）なかった良い性質がある。以下で は、どのようにしてそれが可能であるかを簡単に述べておく。
今、任意の対称型一段法があって、その時間刻みを与える関数として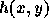 
が与えられているとする。ここで 
はなんでもいいが、これも一段法
である、つまり前のステップの値とかを必要としないものであるとする。
一般に、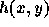 
によって刻み幅を決めて求めていった数値解は、時間反転
に対する対称性を満たしていない。つまり、1ステップ積分してから、逆に戻
すと、タイムステップが変わってしまうためにもとのところに戻らない。この
ことのために、例えば周期軌道の場合に誤差が周期的にならないということが
起こるわけである。
刻み幅を変えつつ時間反転に対する対称性を保つ一つの方法は（これ以外の方
法もあるかもしれないが、今のところ知られていない）、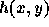 
自体に対
称性を持たせることである。つまり、一段法を
という形に書いた時、
がなりたつことを保証するように h を決めるのである。具体的には、上の 対称性が成り立っていないような時間刻みの式 h があった時に、
によって対称化した時間刻みを作ればいいことになる。この場合時間刻み自体 が陰的に決まることになるが、とにかく対称性という要求は満たされるのであ る。