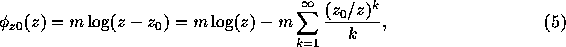
In Anderson's method, the multipole expansion of the potential due to a clump of particles is effectively expressed in terms of the values of potentials on a sphere surrounding the particles. The potential outside the sphere is given by the surface integral on that sphere, which is then approximated by the sum over sampling points. This method, though elegant, appears to be rather indirect.
An alternative approach would be to use multiple particles to represent the multipole expansion. The basic idea here is to place small number of pseudoparticles which reproduce the multipole expansion of the original physical particles. In the following, I first present the theory in two dimensions, and then that in three dimensions.
In two dimensions, the multipole expansion of the gravitational field due to one particle is given by
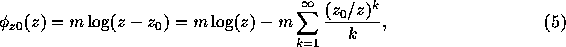
where 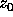 and z are position of the particle and position at which
to evaluate the potential in the complex plane, and m is the mass of
the particle. Here we use the system of units where the gravitational
constant G is unity. This formula converges if
and z are position of the particle and position at which
to evaluate the potential in the complex plane, and m is the mass of
the particle. Here we use the system of units where the gravitational
constant G is unity. This formula converges if 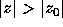 .
.
If we have N particles with mass 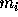 at locations
at locations 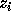 (
(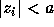 ),
the potential field outside the circle of radius a is expressed as
),
the potential field outside the circle of radius a is expressed as
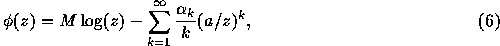
where M is the total mass of particles and 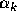 is defined as
is defined as
Our goal is to find an efficient way to place K pseudoparticles to
approximate the potential field 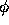 . In theory, the total number of
freedoms we can attain with K particles is 3K. Therefore, with
arbitrary assignment of mass and position, K particles should be
able to represent multipole expansions of up to
. In theory, the total number of
freedoms we can attain with K particles is 3K. Therefore, with
arbitrary assignment of mass and position, K particles should be
able to represent multipole expansions of up to 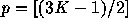 , where
, where
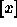 denotes the maximum integer which does not exceed x. However,
in order to determine such an arbitrary distribution of pseudoparticles,
we have to solve the system of nonlinear equations with 2p+1
variables, and the calculation cost would be at least
denotes the maximum integer which does not exceed x. However,
in order to determine such an arbitrary distribution of pseudoparticles,
we have to solve the system of nonlinear equations with 2p+1
variables, and the calculation cost would be at least 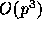 . In
addition, it is not clear whether or not an acceptable solution
exists. In the following, we describe a more systematic approach in
which we do not have to solve nonlinear equations.
. In
addition, it is not clear whether or not an acceptable solution
exists. In the following, we describe a more systematic approach in
which we do not have to solve nonlinear equations.
In Anderson's method, potential is calculated at equispaced points on
a circle. In the same splits, here we place particles in a ring, and
only allow the masses of particles to change. This implies that we use
only K out of 3K degrees of freedoms, and we need 2p+1 particles
to express the multipole expansion coefficients. However, with this
choice we can determine the mass of these 2p+1 particles with
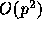 or
or 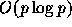 calculation cost.
calculation cost.
Consider the mass distribution of on a ring of radius r. The multipole expansion coefficients is given by

where 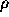 is the line density of mass at polar coordinate
is the line density of mass at polar coordinate
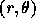 . Thus, from the expansion coefficients
. Thus, from the expansion coefficients 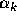 ,
,
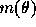 can be calculated by evaluating the Fourier series
can be calculated by evaluating the Fourier series
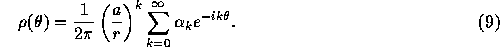
When we approximate this continuous m by 2p+1 discrete points at
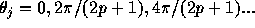 ,
, 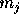 is given by
is given by
Because of the nature of the Fourier series, these 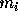 express exact
values of multipole expansions up to p-th order. The potential
outside this circle can be calculated as the sum of the potentials by
these particles as
express exact
values of multipole expansions up to p-th order. The potential
outside this circle can be calculated as the sum of the potentials by
these particles as
where 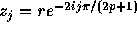 .
.
In the case of the tree algorithm, we can use Eq. (11) to calculate the gravitational interaction between a node and a particle.
In the M2M part, which is the same for both the tree algorithm and FMM, we still have to construct the multipole expansion or particle representation around the center of a node from those of the child nodes. Since the child nodes are already represented by particles, we can use Eq. (7) to obtain the expansion coefficients of the parent node.
Alternatively, we can eliminate the use of multipole expansion
coefficient by calculating the mass of pseudoparticles directly from
mass of physical particles (or the mass of the pseudoparticles in
child nodes). We can derive the formula to calculate 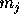 directly
from
directly
from 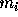 by combining Eqs. (7) and
(10)
by combining Eqs. (7) and
(10)
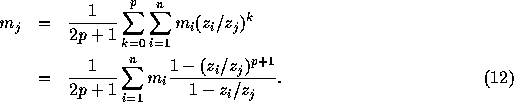
For tree algorithm, this is the end of the story. In the case of FMM, we still have to specify the algorithms for M2L part and L2L part. We can use either Anderson's method or standard harmonic expansion. For local expansion, Anderson's method is simpler to implement than the spherical harmonics.
The formulation for three dimensions is essentially the same as that
for two dimensions, except that we need to use spherical harmonics
instead of 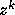 . The expansion coefficients
. The expansion coefficients 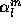 is expressed
as
is expressed
as

where 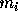 is the mass of particle i and
is the mass of particle i and 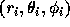 is its polar coordinate. The function
is its polar coordinate. The function 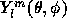 is the
spherical harmonics of degree l, which is expressed as
is the
spherical harmonics of degree l, which is expressed as
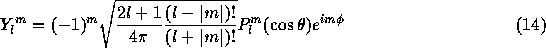
Here, 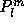 is the associated Legendre function of degree l and
order m. Using these
is the associated Legendre function of degree l and
order m. Using these 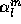 , the potential at position
, the potential at position
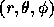 is given by
is given by
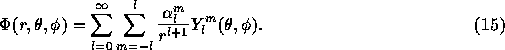
Our goal here is to obtain a mass distribution 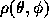 on a sphere of radius
a which satisfy
on a sphere of radius
a which satisfy
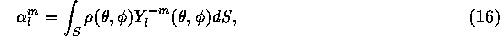
where S denotes the surface of the sphere. Because the spherical
harmonics comprise an orthonormal system, this 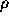 is expressed as
is expressed as

If we use K points on a sphere, their masses are calculated by
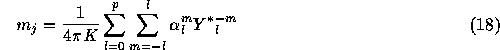
The series expansion must be truncated at a finite value as we've seen
in the case of two dimensions. As discussed by Anderson
[1], the cutoff order must be 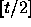 , if K points
form a spherical t-design.
, if K points
form a spherical t-design.
As in the case of two dimensions, we can directly translate the positions and masses of physical particles to that of pseudoparticles. The formal expression is a triple summation over i, l, and m. However, we can simplify it using the addition theorem of spherical harmonics. The addition theorem is
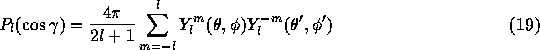
where 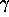 is the angle between two vectors with directions
is the angle between two vectors with directions
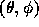 and
and 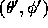 . Using this addition theorem,
. Using this addition theorem,
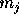 is expressed as
is expressed as

where 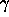 is the angle between the direction of physical particle
i and pseudoparticle j.
is the angle between the direction of physical particle
i and pseudoparticle j.
The potential due to physical particles is approximated by the sum of potentials due to these pseudoparticles.