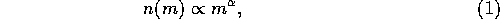
It is generally accepted that the terrestrial planets and the cores of the Jovian planets were formed through the accretion of many small bodies called planetesimals. The accretion process is rather complex, since several competing physical mechanisms are working simultaneously Lissauer1993see e.g.. In particular, the interplay of the velocity distribution and the mass distribution is quite complex.
There have been several numerical studies of the accretion process, in which the coupling between the evolution of the velocity distribution and the mass distribution was taken into account. The importance of the coupling was first pointed out by Greenberg1978. WetherillStewart1989 used the ``particle-in-a-box'' approach with various assumptions for the velocity distribution to study the coupling. They found ``runaway growth'' of massive planetesimals in the simulations which included the effect of the energy equipartition.
KokuboIda1996 performed full three-dimensional N-body simulations of the planetary accretion process, and confirmed that runaway growth takes place. They also found that the mass distribution first relaxes to the power-law form
with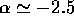 
, for the mass range covered by their
calculation (
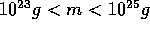). Here, 
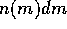gives the surface number density of planetesimals with mass between m and m + dm. Earlier studies based on more
approximate theory (Wetherill and Stewart 1989, 1993, Barge and Pellat
1991, 1993) also showed similar results for that mass range. On the
other hand, in the case of two-dimensional simulations, no simple
power-law mass distribution was realized.
It should be noted that this range of mass
contains most of the mass when the runaway takes place. For masses less than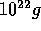 
, planetesimals
exhibit orderly growth, because the condition for the runaway is not
satisfied
OhtsukiIda1990 e.g..
In addition, this power-law mass distribution is realized almost immediately once the runaway starts. Therefore, the same mechanism which drives the runaway growth should be responsible for this power law mass distribution. However, no theoretical explanation has been proposed yet.
In this paper, we present an exact stationary solution of the coagulation equation which explains why the power-law mass distribution is realized in the early stage of the accretion process. In section 2, we derive the exact stationary solution of the coagulation equation. In section 3, we present a more intuitive description of the mechanism of the formation of the power-law distribution. In section 4, we discuss the implications of our result.
