


Next: 3 Interpretation
Up: No Title
Previous: 1 Introduction
The presence of the power-law distribution implies that the evolution
of the mass distribution function 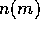 follows an approximately
self-similar solution. Instead of trying to obtain the self-similar
solution, however, here we try to find a stationary solution,
with the supply of the planetesimals at the low-mass end and the
removal of the massive planetesimals at the high-mass end. This is a
usual exercise in studying the distribution function analytically.
follows an approximately
self-similar solution. Instead of trying to obtain the self-similar
solution, however, here we try to find a stationary solution,
with the supply of the planetesimals at the low-mass end and the
removal of the massive planetesimals at the high-mass end. This is a
usual exercise in studying the distribution function analytically.
The change in the surface number density 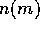 of planetesimals with
mass m is
expressed as
of planetesimals with
mass m is
expressed as
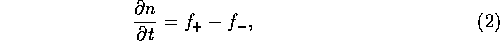
where 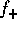 and
and 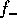 are the incoming and outgoing fluxes. They are
defined as
are the incoming and outgoing fluxes. They are
defined as
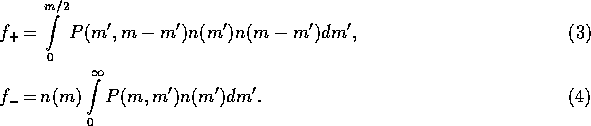
Here, 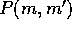 is the probability that two planetesimals of masses
m and
is the probability that two planetesimals of masses
m and 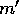 collide in a unit time. This is the classical
Smoluchowski-Safronov coagulation equation [] integrated
over the velocity distribution. The integration over velocity is
justified on the ground that the relaxation timescale is shorter than
the coagulation timescale.
collide in a unit time. This is the classical
Smoluchowski-Safronov coagulation equation [] integrated
over the velocity distribution. The integration over velocity is
justified on the ground that the relaxation timescale is shorter than
the coagulation timescale.
Note that we assume that when two planetesimals collide they always
stick together (perfect accretion). This assumption is okay for
planetesimals since the velocity dispersion is lower
than the escape velocity.
The collision probability 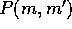 is expressed roughly as
is expressed roughly as
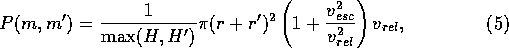
where H is the
scale height, r is the radius of a planetesimal,  is the
escape velocity given by
is the
escape velocity given by
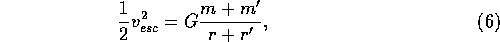
and 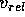 is the average relative velocity given by
is the average relative velocity given by
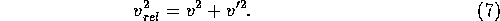
Here G is the gravitational constant.
Note that 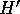 ,
, 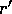 , and
, and 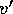 denote corresponding quantities for
the planetesimal of mass
denote corresponding quantities for
the planetesimal of mass 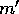 .
.
In the following, we assume that the velocity distribution of the
planetesimals satisfies the thermal equilibrium

and that the velocity is in the extreme gravitational focusing region,
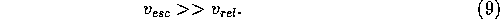
Here we assumed that the two-body formalism can be used to
obtain the collision cross section. This assumption is valid since
the velocity dispersion is in the ``dispersion dominant'' regime
while the runaway growth takes place.
Our goal here is to obtain the mass distribution function 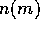 for
which
for
which 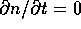 for all values of m. Before trying
to obtain the solution, let us first investigate the characteristics
of the collision probability P. From equations (5)
to (8), we can find the behavior of P in two limiting cases
for all values of m. Before trying
to obtain the solution, let us first investigate the characteristics
of the collision probability P. From equations (5)
to (8), we can find the behavior of P in two limiting cases
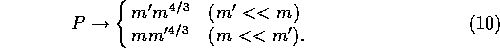
To put it in a slightly different way, we can express P as
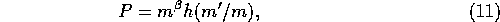
with 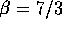 . Here
. Here 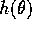 is a function which has the asymptotic behavior of:
is a function which has the asymptotic behavior of:
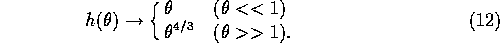
Note that equation (11) combined with equation
(12) is equivalent to equation
(10), but still is exact as long as we
retain the function h.
For the power-law mass distribution of equation
(1), equation (10) implies
that both 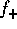 and
and 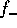 diverge in the low-mass end if
diverge in the low-mass end if 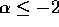 , and
, and 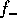 diverges also at the high-mass end if
diverges also at the high-mass end if 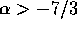 .
In other words, for any value of
.
In other words, for any value of 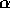 , either of
, either of 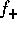 or
or 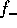 diverges. In particular, for the experimental result of
diverges. In particular, for the experimental result of 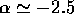 , both diverge at the low-mass end.
, both diverge at the low-mass end.
The divergence at the low-mass end is, however, not a physical
reality, but a mathematical artifact caused by the inadequate form of
equations (3) and
(4). In the limit of 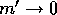 ,
the apparent flux expressed in equations
(3) and
(4) diverges. However, the mass of
particles which originally had a mass of m or
,
the apparent flux expressed in equations
(3) and
(4) diverges. However, the mass of
particles which originally had a mass of m or 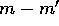 does not change
in the limit of
does not change
in the limit of 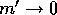 . In other words, there is an
infinite flux, in between the two mass bins with infinitesimal
separation. The net effect of the product of the infinite and the
infinitesimal must be carefully examined.
. In other words, there is an
infinite flux, in between the two mass bins with infinitesimal
separation. The net effect of the product of the infinite and the
infinitesimal must be carefully examined.
A convenient way to avoid this difficulty of the apparent divergence
of f is to introduce the ``mass flux'' F, in such a way that its
partial derivative in mass space gives the net change of the
distribution function as
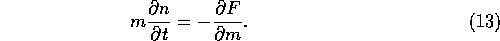
Tanakaetal1996 used this form to study the collision cascade
process. The formal derivation here is essentially the same as theirs.
Since equation (13) implies that F is
the integral
of 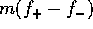 , one might think it should behave in exactly the same
way. However, as we'll see shortly, F does not diverge at the
low-mass end, even though
, one might think it should behave in exactly the same
way. However, as we'll see shortly, F does not diverge at the
low-mass end, even though 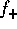 and
and 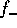 diverge. This is because
the contribution of the low-mass end to the mass flux F is small. As
we stated earlier, the change of mass vanishes at the low-mass
end. Thus, even though
diverge. This is because
the contribution of the low-mass end to the mass flux F is small. As
we stated earlier, the change of mass vanishes at the low-mass
end. Thus, even though 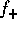 and
and 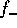 diverge, their contribution to
F vanishes at the low-mass end.
diverge, their contribution to
F vanishes at the low-mass end.
The mass flux F is calculated as
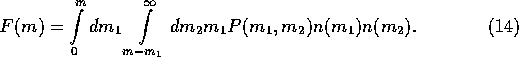
It is straightforward to prove that the combination of equations
(13) and (14) is formally
equivalent to equations (2) through
(4).
As shown by Tanakaetal1996, for a
collision rate of the form of equation (11),
F is reduced to
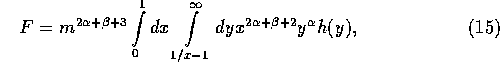
where 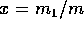 and
and 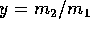 .
.
The stationary solution corresponds to the case 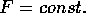 ,
which is realized when
,
which is realized when
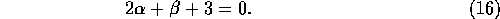
As stressed by Tanakaetal1996 this result does not depend on the
functional form of 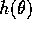 , as far as
, as far as 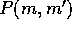 can be expressed in the
form of equation (11).
can be expressed in the
form of equation (11).
The double integral in equation (15) should have a finite
value. To determine if it is the case or not, it is more convenient to
rewrite the double integral in a slightly different form as
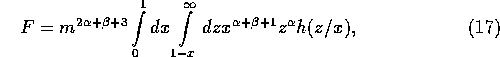
where 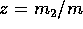 .
.
Without losing generality, we can assume that h has the following
asymptotic expression
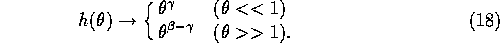
Since 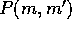 is symmetric, the limiting behavior of h in either
limit determines the behavior in the other limit. Equation
(12) corresponds to the case of
is symmetric, the limiting behavior of h in either
limit determines the behavior in the other limit. Equation
(12) corresponds to the case of 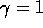 .
.
The condition that F is finite is given by

The first inequality comes from the condition that the integrand
should approach zero faster than 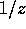 in the limit of
in the limit of 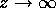 . The second comes from the condition that the integrand should
not diverge as
. The second comes from the condition that the integrand should
not diverge as 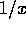 or faster in the limit of
or faster in the limit of 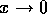 . This
inequality also guarantees that the integrand does
not diverge as
. This
inequality also guarantees that the integrand does
not diverge as 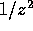 or faster in the limit of
or faster in the limit of 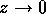 . Note that it can diverge faster than
. Note that it can diverge faster than 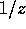 , since the range of the
integration over x is proportional to z.
, since the range of the
integration over x is proportional to z.
The criterion (19) is different from what
is shown in the Appendix of Tanakaetal1996. Their
derivation did not incorporate the effect of the power of h on the convergence criterion correctly.
For 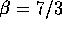 , we have
, we have 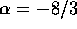 . As noted above,
. As noted above, 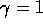 . This set of values satisfies the convergence criteria. Thus,
we found a stationary solution of the coagulation equation expressed
as
. This set of values satisfies the convergence criteria. Thus,
we found a stationary solution of the coagulation equation expressed
as 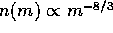 . This is in quite good agreement with the
numerical results obtained by N-body or Fokker-Planck calculations.
. This is in quite good agreement with the
numerical results obtained by N-body or Fokker-Planck calculations.



Next: 3 Interpretation
Up: No Title
Previous: 1 Introduction
Jun Makino
Thu Jul 2 18:05:36 JST 1998
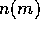 follows an approximately
self-similar solution. Instead of trying to obtain the self-similar
solution, however, here we try to find a stationary solution,
with the supply of the planetesimals at the low-mass end and the
removal of the massive planetesimals at the high-mass end. This is a
usual exercise in studying the distribution function analytically.
follows an approximately
self-similar solution. Instead of trying to obtain the self-similar
solution, however, here we try to find a stationary solution,
with the supply of the planetesimals at the low-mass end and the
removal of the massive planetesimals at the high-mass end. This is a
usual exercise in studying the distribution function analytically.
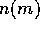 of planetesimals with
mass m is
expressed as
of planetesimals with
mass m is
expressed as
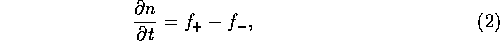
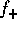 and
and 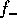 are the incoming and outgoing fluxes. They are
defined as
are the incoming and outgoing fluxes. They are
defined as
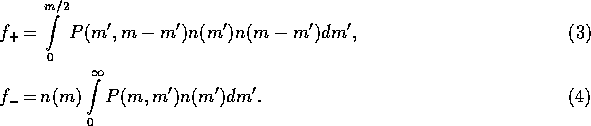
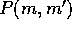 is the probability that two planetesimals of masses
m and
is the probability that two planetesimals of masses
m and 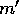 collide in a unit time. This is the classical
Smoluchowski-Safronov coagulation equation [
collide in a unit time. This is the classical
Smoluchowski-Safronov coagulation equation [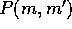 is expressed roughly as
is expressed roughly as
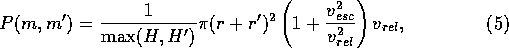
 is the
escape velocity given by
is the
escape velocity given by
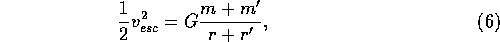
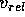 is the average relative velocity given by
is the average relative velocity given by
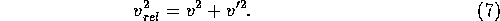
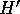 ,
, 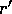 , and
, and 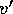 denote corresponding quantities for
the planetesimal of mass
denote corresponding quantities for
the planetesimal of mass 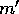 .
.

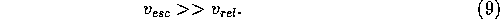
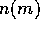 for
which
for
which  for all values of m. Before trying
to obtain the solution, let us first investigate the characteristics
of the collision probability P. From equations (
for all values of m. Before trying
to obtain the solution, let us first investigate the characteristics
of the collision probability P. From equations (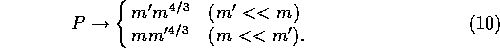
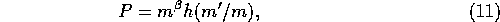
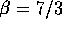 . Here
. Here 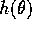 is a function which has the asymptotic behavior of:
is a function which has the asymptotic behavior of:
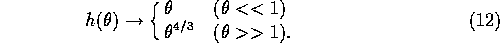
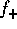 and
and 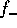 diverge in the low-mass end if
diverge in the low-mass end if 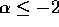 , and
, and 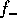 diverges also at the high-mass end if
diverges also at the high-mass end if 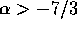 .
In other words, for any value of
.
In other words, for any value of 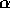 , either of
, either of 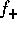 or
or 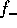 diverges. In particular, for the experimental result of
diverges. In particular, for the experimental result of 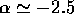 , both diverge at the low-mass end.
, both diverge at the low-mass end.
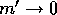 ,
the apparent flux expressed in equations
(
,
the apparent flux expressed in equations
(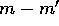 does not change
in the limit of
does not change
in the limit of 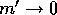 . In other words, there is an
infinite flux, in between the two mass bins with infinitesimal
separation. The net effect of the product of the infinite and the
infinitesimal must be carefully examined.
. In other words, there is an
infinite flux, in between the two mass bins with infinitesimal
separation. The net effect of the product of the infinite and the
infinitesimal must be carefully examined.
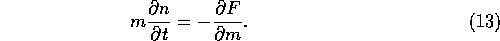
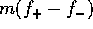 , one might think it should behave in exactly the same
way. However, as we'll see shortly, F does not diverge at the
low-mass end, even though
, one might think it should behave in exactly the same
way. However, as we'll see shortly, F does not diverge at the
low-mass end, even though 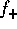 and
and 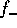 diverge. This is because
the contribution of the low-mass end to the mass flux F is small. As
we stated earlier, the change of mass vanishes at the low-mass
end. Thus, even though
diverge. This is because
the contribution of the low-mass end to the mass flux F is small. As
we stated earlier, the change of mass vanishes at the low-mass
end. Thus, even though 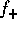 and
and 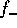 diverge, their contribution to
F vanishes at the low-mass end.
diverge, their contribution to
F vanishes at the low-mass end.
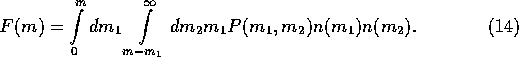
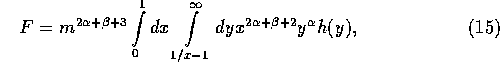
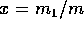 and
and 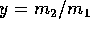 .
.
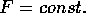 ,
which is realized when
,
which is realized when
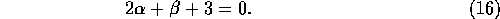
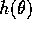 , as far as
, as far as 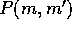 can be expressed in the
form of equation (
can be expressed in the
form of equation (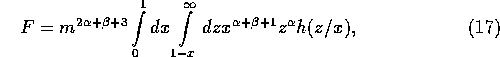
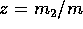 .
.
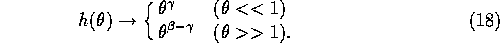
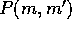 is symmetric, the limiting behavior of h in either
limit determines the behavior in the other limit. Equation
(
is symmetric, the limiting behavior of h in either
limit determines the behavior in the other limit. Equation
(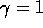 .
.

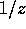 in the limit of
in the limit of 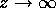 . The second comes from the condition that the integrand should
not diverge as
. The second comes from the condition that the integrand should
not diverge as 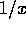 or faster in the limit of
or faster in the limit of 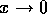 . This
inequality also guarantees that the integrand does
not diverge as
. This
inequality also guarantees that the integrand does
not diverge as 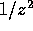 or faster in the limit of
or faster in the limit of 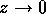 . Note that it can diverge faster than
. Note that it can diverge faster than 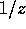 , since the range of the
integration over x is proportional to z.
, since the range of the
integration over x is proportional to z.
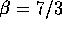 , we have
, we have 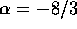 . As noted above,
. As noted above, 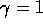 . This set of values satisfies the convergence criteria. Thus,
we found a stationary solution of the coagulation equation expressed
as
. This set of values satisfies the convergence criteria. Thus,
we found a stationary solution of the coagulation equation expressed
as 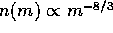 . This is in quite good agreement with the
numerical results obtained by N-body or Fokker-Planck calculations.
. This is in quite good agreement with the
numerical results obtained by N-body or Fokker-Planck calculations.