


Next: 4 Discussion and summary
Up: No Title
Previous: 2 Theory
Though the result obtained in the previous section is simple and in
good agreement with the experimental result, the mechanism which
determines the value of 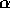 is not at all clear. In this section,
we try to determine
is not at all clear. In this section,
we try to determine 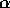 with more approximate approaches and to
obtain qualitative understanding. First,
we obtain the growth rate and growth mode of a typical
planetesimal, using the collision probability obtained in section
2, and then derive the stationary distribution from
them.
with more approximate approaches and to
obtain qualitative understanding. First,
we obtain the growth rate and growth mode of a typical
planetesimal, using the collision probability obtained in section
2, and then derive the stationary distribution from
them.
The growth rate of a planetesimal is obtained by
integrating equation (5) over the range 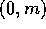 as
Safronov1969,BargePellat1991 e.g.
as
Safronov1969,BargePellat1991 e.g.
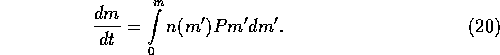
By substituting equations (5) through (8)
into equation (20) and neglecting the dependence on 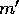 of
of  and r and that on m of
and r and that on m of 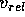 , we have
, we have
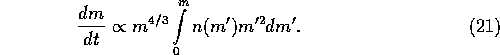
For the power-law mass distribution of equation (1),
equation (21) is reduced to
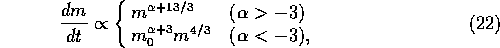
where 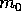 is the cut-off mass of the distribution function at the
low-mass end. These two cases correspond to two different modes of
accretion. If
is the cut-off mass of the distribution function at the
low-mass end. These two cases correspond to two different modes of
accretion. If  , the main mode of the growth is to eat
small planetesimals, since the growth rate is determined by the low
end of the integration over mass. If
, the main mode of the growth is to eat
small planetesimals, since the growth rate is determined by the low
end of the integration over mass. If 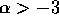 , on the other hand,
the growth is driven by the collision with particles with similar
masses. In other words, the growth is hierarchical.
, on the other hand,
the growth is driven by the collision with particles with similar
masses. In other words, the growth is hierarchical.
Both the numerical results and the result obtained in the previous
section suggest that 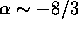 . So we consider the case
. So we consider the case
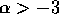 . The stationary state is realized if the mass flux
does not depend on either the time or the mass, which
is expressed as
. The stationary state is realized if the mass flux
does not depend on either the time or the mass, which
is expressed as

Note that here the condition of the stationary distribution is the
constant flux of the mass nm, and not the constant flux of the number
of planetesimals n. This is because the dominant mode of the growth
of the planetesimals is the hierarchical growth. The number of
planetesimals would become smaller as they grow, since growth is
driven by collisions of planetesimals of similar sizes.
If collisions are dominantly hierarchical, strictly speaking it
does not make sense to use the growth equation expressed as the
differential equation (20), since the change of the mass of
planetesimals is not continuous. However, in this case we can use the
mass doubling timescale
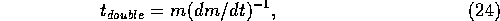
and
consider the discrete mass bins with the ranges 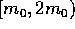 ,
,
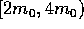 ,
,  , ...
, ... 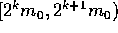 ,
... In this picture, collisions take place only between
particles in the same mass bins. The product of the collision
moves to the next mass bin.
,
... In this picture, collisions take place only between
particles in the same mass bins. The product of the collision
moves to the next mass bin.
In this case, the stationary state is realized when the incoming and
outgoing flux for each mass bin are equal. For mass bin
k, the total mass of planetesimals lost per unit time is
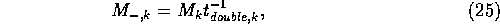
where the subscript k denotes the mass bin k and 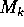 is the
total mass of planetesimals in the mass bin k. Note that
is the
total mass of planetesimals in the mass bin k. Note that 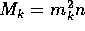 , since the width of the mass bin is proportional to m itself.
, since the width of the mass bin is proportional to m itself.
The incoming mass to bin k is what is lost from bin k-1. Thus, the
condition for the stationary state is that the outgoing mass is the
same for all mass bins,
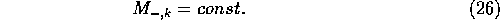
Equations (24) through (26) leads to
equation (23) as the condition for the stationary
state. Thus, whether we assume
continuous growth of the mass or discontinuous jumps in the mass, the
condition for the stationary state is the same.
From equation (1), (22), and (23),
we obtain
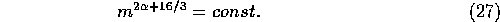
and therefore

This value is the same as we obtained in
section
2.
If we assume a constant flux of the number of
planetesimals, we obtain 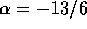 , which is significantly
smaller.
, which is significantly
smaller.
The reason why 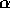 has a large negative value is now clear. As can
be seen in equation (22), the growth rate of planetesimals
has a strong positive dependence on their mass. This is, of course,
why the runaway growth occurs [].
This strong
dependence requires that the number of planetesimal goes down quickly
as its mass increases, if a stationary distribution is to be
realized. The strong dependence of the growth rate on the mass comes
from the size, scale height and the effect of gravitational focusing,
all of which enhance the growth rate for larger mass.
has a large negative value is now clear. As can
be seen in equation (22), the growth rate of planetesimals
has a strong positive dependence on their mass. This is, of course,
why the runaway growth occurs [].
This strong
dependence requires that the number of planetesimal goes down quickly
as its mass increases, if a stationary distribution is to be
realized. The strong dependence of the growth rate on the mass comes
from the size, scale height and the effect of gravitational focusing,
all of which enhance the growth rate for larger mass.
From equations (22) and (28), we obtain
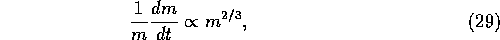
which implies the mass of a planetesimal can reach infinity in a
finite time. Of course, this cannot happen in reality, since the
number of planetesimals with this infinite mass would go below unity.
In addition, at a certain point the most massive particle grows so
massive that its effect dominates the velocity dispersion of less
massive particles, resulting in the slowing down of the growth
[]. This slowing down causes the massive
planetesimals of similar mass to be formed in roughly equal orbital
separation. Thus, these massive particles cannot collide with each
other []. Nevertheless, equation (29)
implies that the stationary distribution of the mass for a wide range
of masses can be realized in a short time.
It should be noted that the growth rate of equation (29)
is larger than what has been used for the timescale estimate for the
runaway stage (see . e.g., Ida and Makino 1993). In previous
estimates, uniform background distribution of planetesimals was
assumed. Under this assumption, the power of m in equation
(29) becomes 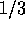 .
.
In the case of the two-dimensional space, equation
(5) becomes
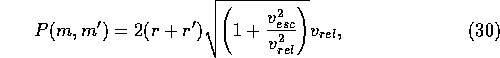
which gives 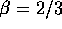 . Therefore. from equation
(16) we obtain
. Therefore. from equation
(16) we obtain

However, with this formula, the total mass diverges if the high-mass
end is taken infinite. Therefore, for the total mass to conserve,
there must be a cutoff at the high-mass end, and
no stationary solution is possible. In other words, the growth would
be an orderly one.
The value of 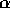 for two-dimensional case coincides with that for
collisional cascade []. This is simply because the
value of
for two-dimensional case coincides with that for
collisional cascade []. This is simply because the
value of 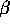 is the same.
is the same.
Note that the existence of the stationary solution is directly related
to the occurrence of the runaway growth. The runaway implies that the
heavy particles can become heavier by themselves, without being
affected by lighter particles. Thus, the power-law behavior is
observed because there is no characteristic scale. In the case of the
two-dimensional simulation, the evolution of the heaviest particle is
slower than that of lighter particles, and therefore all particles
tend to have a mass similar to that of the heaviest
particle. The power-law behavior is not observed in this case.



Next: 4 Discussion and summary
Up: No Title
Previous: 2 Theory
Jun Makino
Thu Jul 2 18:05:36 JST 1998
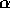 is not at all clear. In this section,
we try to determine
is not at all clear. In this section,
we try to determine 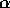 with more approximate approaches and to
obtain qualitative understanding. First,
we obtain the growth rate and growth mode of a typical
planetesimal, using the collision probability obtained in section
2, and then derive the stationary distribution from
them.
with more approximate approaches and to
obtain qualitative understanding. First,
we obtain the growth rate and growth mode of a typical
planetesimal, using the collision probability obtained in section
2, and then derive the stationary distribution from
them.
 as
Safronov1969,BargePellat1991 e.g.
as
Safronov1969,BargePellat1991 e.g.
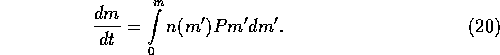
 of
of  and r and that on m of
and r and that on m of  , we have
, we have
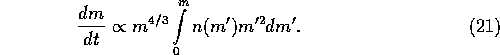
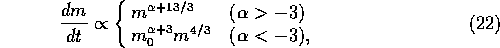
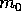 is the cut-off mass of the distribution function at the
low-mass end. These two cases correspond to two different modes of
accretion. If
is the cut-off mass of the distribution function at the
low-mass end. These two cases correspond to two different modes of
accretion. If  , the main mode of the growth is to eat
small planetesimals, since the growth rate is determined by the low
end of the integration over mass. If
, the main mode of the growth is to eat
small planetesimals, since the growth rate is determined by the low
end of the integration over mass. If 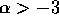 , on the other hand,
the growth is driven by the collision with particles with similar
masses. In other words, the growth is hierarchical.
, on the other hand,
the growth is driven by the collision with particles with similar
masses. In other words, the growth is hierarchical.
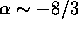 . So we consider the case
. So we consider the case
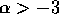 . The stationary state is realized if the mass flux
does not depend on either the time or the mass, which
is expressed as
. The stationary state is realized if the mass flux
does not depend on either the time or the mass, which
is expressed as

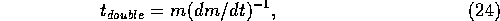
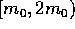 ,
,
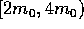 ,
,  , ...
, ... 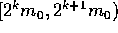 ,
... In this picture, collisions take place only between
particles in the same mass bins. The product of the collision
moves to the next mass bin.
,
... In this picture, collisions take place only between
particles in the same mass bins. The product of the collision
moves to the next mass bin.
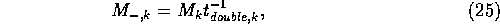
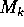 is the
total mass of planetesimals in the mass bin k. Note that
is the
total mass of planetesimals in the mass bin k. Note that 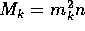 , since the width of the mass bin is proportional to m itself.
, since the width of the mass bin is proportional to m itself.
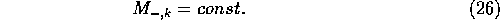
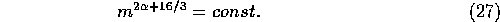

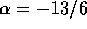 , which is significantly
smaller.
, which is significantly
smaller.
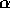 has a large negative value is now clear. As can
be seen in equation (
has a large negative value is now clear. As can
be seen in equation (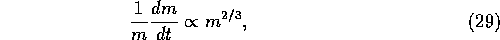
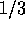 .
.
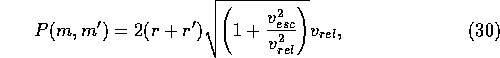
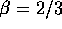 . Therefore. from equation
(
. Therefore. from equation
(
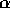 for two-dimensional case coincides with that for
collisional cascade [
for two-dimensional case coincides with that for
collisional cascade [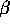 is the same.
is the same.