


Next: 2. Direct simulation of
Up: Direct Simulation of Dense
Previous: Direct Simulation of Dense
Direct N-body simulation of star clusters or other stellar systems
has proven itself an extremely powerful tool to study the structure
and evolution of stellar systems, since the pioneering work by von
Hörner ([1960,1963]). The only known way to
do experiments on stellar systems is to construct their models in
computers, because we cannot do laboratory experiments on stellar
systems,
Of course, N-body simulation is not the only way to construct
computer models of star clusters. One could use Monte-Carlo (Henon
[1971], for recent development see Giersz [1998])
or direct integration of Fokker-Planck (FP) equations (Cohn
[1980], Takahashi [1996], Drukier et al.
[1999]). In particular, recent advance in the
treatment of the two-dimensional [f(E,J)] FP equation made it
possible to use FP code to the study of the evaporation of clusters in
the tidal field of the parent galaxy.
The main advantage of these methods over direct N-body simulation is
the calculation cost. While it is still out of reach to perform the
direct simulation of, say, a typical globular cluster with 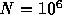 ,
the FP equation is valid in the limit of
,
the FP equation is valid in the limit of 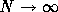 . Therefore, when the assumption of large-N limit is good,
methods based on the FP approximation can deliver reliable results for
the calculation cost orders of magnitudes smaller than that of direct
N-body calculation. In principle, one can do the N-body simulation
with small N and then try to extrapolate that result to larger
N. However, this problem, which is sometimes called ``the scaling
problem'' has proven itself a complex and difficult
problem(Heggie et al. [1998]). The main reason of the difficulty is
that there are many physical processes of which timescales depend on
the number of particles in different ways, and that there is no way to
adjust all relevant timescales consistently.
. Therefore, when the assumption of large-N limit is good,
methods based on the FP approximation can deliver reliable results for
the calculation cost orders of magnitudes smaller than that of direct
N-body calculation. In principle, one can do the N-body simulation
with small N and then try to extrapolate that result to larger
N. However, this problem, which is sometimes called ``the scaling
problem'' has proven itself a complex and difficult
problem(Heggie et al. [1998]). The main reason of the difficulty is
that there are many physical processes of which timescales depend on
the number of particles in different ways, and that there is no way to
adjust all relevant timescales consistently.
On the other hand, methods based on FP approximation do have their own
limitations. For example, it's pretty difficult to extend the
formulation beyond the spherical symmetry. Moreover, they also suffer
the problem of the time scaling, only difference is that they are
affected from the opposite direction. For example, when we want to
include the dynamical effect of the slowly varying potential, FP
approximation goes into trouble. Consider the tidal stripping of
globular clusters with non-circular orbit. The orbital timescale is of
the order of 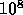 years. The orbital timescale of the stars around
the tidal boundary of the cluster is also
years. The orbital timescale of the stars around
the tidal boundary of the cluster is also 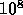 years. On the other
hand, the half-mass relaxation time is of the order of
years. On the other
hand, the half-mass relaxation time is of the order of 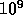 years. Therefore, the timestep to integrate the FP equation is at
the largest
years. Therefore, the timestep to integrate the FP equation is at
the largest 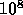 years, and in practice much smaller than that. Clearly,
the assumption that the dynamical timescale is smaller than the
Fokker-Plank timestep is broken, and FP calculations tends to grossly
overestimate the escaper rate.
years, and in practice much smaller than that. Clearly,
the assumption that the dynamical timescale is smaller than the
Fokker-Plank timestep is broken, and FP calculations tends to grossly
overestimate the escaper rate.
As beautifully demonstrated by Takahashi and Portegies Zwart
([1998]), one can incorporate the escaping
timescale into FP calculation. However, in order to do so the model
parameter must be adjusted so that the agreement with reference
N-body calculations is achieved. Moreover, this agreement has been
so far achieved only with N-body simulations with simple static
``tidal cutoff'', where no tidal field is imposed and stars
outside the tidal radius are just removed. Whether or not FP
calculations can reproduce the result of N-body calculations with
tidal fields is an open question.
The ultimate solution for the scaling problem is to perform N-body
simulations with sufficiently large number of particles. In the first
half of this paper, we describe our effort in that direction, the
GRAPE project to develop and use special-purpose computers for
N-body simulations. In the last half of this paper, we'd like to
discuss briefly our recent work on N-body simulations of galactic
centers with massive black holes, where again the scaling problem
shows up.



Next: 2. Direct simulation of
Up: Direct Simulation of Dense
Previous: Direct Simulation of Dense
Jun Makino
Fri Jul 7 14:45:07 JST 2000
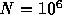 ,
the FP equation is valid in the limit of
,
the FP equation is valid in the limit of 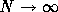 . Therefore, when the assumption of large-N limit is good,
methods based on the FP approximation can deliver reliable results for
the calculation cost orders of magnitudes smaller than that of direct
N-body calculation. In principle, one can do the N-body simulation
with small N and then try to extrapolate that result to larger
N. However, this problem, which is sometimes called ``the scaling
problem'' has proven itself a complex and difficult
problem(Heggie et al. [1998]). The main reason of the difficulty is
that there are many physical processes of which timescales depend on
the number of particles in different ways, and that there is no way to
adjust all relevant timescales consistently.
. Therefore, when the assumption of large-N limit is good,
methods based on the FP approximation can deliver reliable results for
the calculation cost orders of magnitudes smaller than that of direct
N-body calculation. In principle, one can do the N-body simulation
with small N and then try to extrapolate that result to larger
N. However, this problem, which is sometimes called ``the scaling
problem'' has proven itself a complex and difficult
problem(Heggie et al. [1998]). The main reason of the difficulty is
that there are many physical processes of which timescales depend on
the number of particles in different ways, and that there is no way to
adjust all relevant timescales consistently.
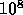 years. The orbital timescale of the stars around
the tidal boundary of the cluster is also
years. The orbital timescale of the stars around
the tidal boundary of the cluster is also 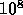 years. On the other
hand, the half-mass relaxation time is of the order of
years. On the other
hand, the half-mass relaxation time is of the order of 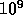 years. Therefore, the timestep to integrate the FP equation is at
the largest
years. Therefore, the timestep to integrate the FP equation is at
the largest 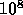 years, and in practice much smaller than that. Clearly,
the assumption that the dynamical timescale is smaller than the
Fokker-Plank timestep is broken, and FP calculations tends to grossly
overestimate the escaper rate.
years, and in practice much smaller than that. Clearly,
the assumption that the dynamical timescale is smaller than the
Fokker-Plank timestep is broken, and FP calculations tends to grossly
overestimate the escaper rate.