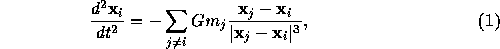
In principle, the direct N-body simulation of stellar systems is very simple and straightforward. The only thing one has to do is to numerically integrate the following system of equations of motion:
where 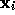 and
and 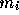 are the position and mass of the particle with
index i and G is the gravitational constant. The summation is
taken over all stars in the system.
are the position and mass of the particle with
index i and G is the gravitational constant. The summation is
taken over all stars in the system.
In practice, we need complex methods and tricks to integrate the above equation. Since we cannot cover all important issues here, we recommend the reviews by Spurzem ([1999]) and Aarseth ([1999a,1999b]). Here, we briefly discuss issues directly related to the use of special-purpose hardwares for N-body problem.
As we wrote above, in principle an N-body simulation is simple and straightforward. At each timestep, we calculate the forces on all particles in the system, and integrate their orbits using some appropriate integration method. In fact, in Molecular Dynamics simulation, where one solves the N-body problem of atoms interacting through Coulomb and van der Waals forces, one can rely on this approach. In astrophysics, however, the nature of the gravitational interaction makes such approach impractical.
The problem is that the gravitational force is an attractive force with no characteristic scale length. This fact leads to three complications. The first one is that the inhomogeneity develops as the system evolves. In the case of star clusters, this is known as core collapse or gravitational catastrophe. The central core of the cluster evolves to higher and higher density, while its mass decreases. The timestep has to be small enough to integrate accurately the orbits of particles in the core. Therefore, the timestep decreases as the cluster evolves. The second one is that even when the core density is not very high, random close encounters of two particles can lead to arbitrary short timesteps. The third one is that stable binaries and more complex hierarchical systems are formed through three-body encounters and encounters of larger number of particles (such as binary-binary interactions). These systems have very small orbital timescales. For a quantitative analysis of these issues, see Makino and Hut ([1988,1990]).
Fortunately, we can handle these complications by a combination of techniques. The first two are solved by assigning each particle its own time and timestep. This scheme, the individual timestep scheme, was first introduced by Aarseth ([1963]), and has been used for four decades.
In the individual timestep scheme, each particle has its own timestep
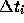 and maintains its own time
and maintains its own time 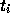 . To integrate the
system, one first selects the particle for which the next time (
. To integrate the
system, one first selects the particle for which the next time (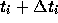 ) is the minimum. Then, one predicts its position at this
new time. Positions of all other particles at this time must be
predicted also. Then the force on that particle from other particles
is calculated. The position and velocity of the particle is then
corrected. The new timestep is also calculated. The integration
scheme is a variation of Krogh's scheme (Krogh [1974])
modified for second-order equations.
) is the minimum. Then, one predicts its position at this
new time. Positions of all other particles at this time must be
predicted also. Then the force on that particle from other particles
is calculated. The position and velocity of the particle is then
corrected. The new timestep is also calculated. The integration
scheme is a variation of Krogh's scheme (Krogh [1974])
modified for second-order equations. ![]()
A modification of this individual timestep algorithm is now used to achieve higher efficiency on vector machines (McMillan [1986]) and special-purpose computers (Makino [1991a]). This scheme is called the blockstep scheme. In this scheme, the timesteps of particles are forced to integer powers of two. In addition, the new timestep of a particle is chosen so that the time of the particle is an integer multiple of the new timestep. These two criteria make it possible to force multiple particles to share exactly the same time. As a result, the efficiency of vector/parallel hardware is improved significantly. However, it should be noted that the average number of particles which share the same time is not very large, in particular when the central core is small and dense. Therefore, it is necessary that the force calculation procedure can achieve reasonable performance when the number of particles to be integrated in parallel is small. Since the number of particles in the core can be as small as 100 or less, it is necessary that the force calculation procedure can achieve a reasonable speed for that number.
The third problem, the stable binaries and other hierarchical systems, is solved essentially by integrating them as small-N subsystem embedded in the cluster. The motion of the center of mass of the subsystem and internal motion of its members are separated, and integrated independently with different timesteps. If the perturbations from the rest of the system is small, we can ignore it. In the case of a binary, this means we can completely skip the numerical integration of the internal motion, since we know the analytic solution. If the perturbation is not negligible but is small, we can apply various techniques such as ``Slow KS'' (Mikkola and Aarseth [1996]). Here, the hardest problem is not really the calculation cost. The challenge is how we can recognize these subsystems and their internal structures, and how we can decide what method is appropriate for that particular structure.